poj 3498 最大流

March of the Penguins

Time Limit: 8000MS		Memory Limit: 65536K
Total Submissions: 4809		Accepted: 2195

Description

Somewhere near the south pole, a number of penguins are standing on a number of ice floes. Being social animals, the penguins would like to get together, all on the same floe. The penguins do not want to get wet, so they have use their limited jump distance to get together by jumping from piece to piece. However, temperatures have been high lately, and the floes are showing cracks, and they get damaged further by the force needed to jump to another floe. Fortunately the penguins are real experts on cracking ice floes, and know exactly how many times a penguin can jump off each floe before it disintegrates and disappears. Landing on an ice floe does not damage it. You have to help the penguins find all floes where they can meet.

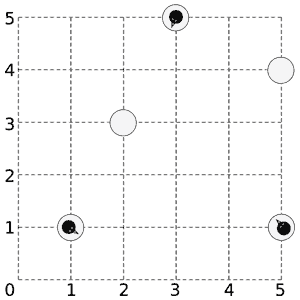
A sample layout of ice floes with 3 penguins on them.

Input

On the first line one positive number: the number of testcases, at most 100. After that per testcase:

• One line with the integer N (1 ≤ N ≤ 100) and a floating-point number D (0 ≤ D ≤ 100 000), denoting the number of ice pieces and the maximum distance a penguin can jump.

• N lines, each line containing x_i, y_i, n_i and m_i, denoting for each ice piece its X and Y coordinate, the number of penguins on it and the maximum number of times a penguin can jump off this piece before it disappears (−10 000 ≤ x_i, y_i ≤ 10 000, 0 ≤ n_i ≤ 10, 1 ≤ m_i ≤ 200).

Output

Per testcase:

• One line containing a space-separated list of 0-based indices of the pieces on which all penguins can meet. If no such piece exists, output a line with the single number −1.

Sample Input

2
5 3.5
1 1 1 1
2 3 0 1
3 5 1 1
5 1 1 1
5 4 0 1
3 1.1
-1 0 5 10
0 0 3 9
2 0 1 1

Sample Output

1 2 4
-1

Source

Northwestern Europe 2007

题意：

在二维坐标内有n块冰块，每只企鹅最远能跳d的距离，给出每块冰块的位置，该冰块上最初企鹅的个数以及该冰块最多能承受几个企鹅从此处跳走，求出可以把所有的企鹅都集合起来的冰块，输出冰块序号（冰块上能承受无数多企鹅，但跳出去的数量有限制）

代码：

//枚举汇点+拆点，两点之间的距离>=d的建边，然后最大流
#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
#include<queue>
#include<cmath>
using namespace std;
const int maxn=;
const int inf=0x7fffffff;
double mp[maxn][maxn];
struct Edge{
    int from,to,cap,flow;
    Edge(int u,int v,int c,int f):from(u),to(v),cap(c),flow(f){}
};
struct Dinic{
    int n,m,s,t;
    vector<Edge>edges;
    vector<int>g[maxn];
    bool vis[maxn];
    int d[maxn];
    int cur[maxn];
    void Init(int n){
        this->n=n;
        for(int i=;i<n;i++) g[i].clear();
        edges.clear();
    }
    void Addedge(int from,int to,int cap){
        edges.push_back(Edge(from,to,cap,));
        edges.push_back(Edge(to,from,,));//反向弧
        m=edges.size();
        g[from].push_back(m-);
        g[to].push_back(m-);
    }
    bool Bfs(){
        memset(vis,,sizeof(vis));
        queue<int>q;
        q.push(s);
        d[s]=;
        vis[s]=;
        while(!q.empty()){
            int x=q.front();q.pop();
            for(int i=;i<(int)g[x].size();i++){
                Edge &e=edges[g[x][i]];
                if(!vis[e.to]&&e.cap>e.flow){
                    vis[e.to]=;
                    d[e.to]=d[x]+;
                    q.push(e.to);
                }
            }
        }
        return vis[t];
    }
    int Dfs(int x,int a){
        if(x==t||a==) return a;
        int flow=,f;
        for(int&i=cur[x];i<(int)g[x].size();i++){
            Edge &e=edges[g[x][i]];
            if(d[x]+==d[e.to]&&(f=Dfs(e.to,min(a,e.cap-e.flow)))>){
                e.flow+=f;
                edges[g[x][i]^].flow-=f;
                flow+=f;
                a-=f;
                if(a==) break;
            }
        }
        return flow;
    }
    int Maxflow(int s,int t){
        this->s=s;this->t=t;
        int flow=;
        while(Bfs()){
            memset(cur,,sizeof(cur));
            flow+=Dfs(s,inf);
        }
        return flow;
    }
}dc;
int main()
{
    int n,t,peng[maxn],tim[maxn];
    double d,x[maxn],y[maxn];
    scanf("%d",&t);
    while(t--){
        scanf("%d%lf",&n,&d);
        int sum=;
        for(int i=;i<=n;i++){
            scanf("%lf%lf%d%d",&x[i],&y[i],&peng[i],&tim[i]);
            sum+=peng[i];
            for(int j=;j<=i;j++){
                double dis=sqrt((x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j]));
                mp[i][j]=mp[j][i]=dis;
            }
        }
        int ans[],cnt=;
        for(int i=;i<=n;i++){
            dc.Init(*n+);
            for(int j=;j<=n;j++){
                if(j==i) continue;
                dc.Addedge(j,j+n,tim[j]);
                dc.Addedge(,j,peng[j]);
                for(int k=;k<=n;k++) if(mp[j][k]<=d)
                    dc.Addedge(j+n,k,inf);
            }
            if(dc.Maxflow(,i)==sum-peng[i]) ans[cnt++]=i-;
        }
        if(cnt==) printf("-1\n");
        else{
            for(int i=;i<cnt-;i++) printf("%d ",ans[i]);
            printf("%d\n",ans[cnt-]);
        }
    }
    return ;
}