(中等) POJ 1084 Square Destroyer , DLX+可重复覆盖。

　　Description

　　The left figure below shows a complete 3*3 grid made with 2*(3*4) (=24) matchsticks. The lengths of all matchsticks are one. You can find many squares of different sizes in the grid. The size of a square is the length of its side. In the grid shown in the left figure, there are 9 squares of size one, 4 squares of size two, and 1 square of size three.

　　Each matchstick of the complete grid is identified with a unique number which is assigned from left to right and from top to bottom as shown in the left figure. If you take some matchsticks out from the complete grid, then some squares in the grid will be destroyed, which results in an incomplete 3*3 grid. The right figure illustrates an incomplete 3*3 grid after removing three matchsticks numbered with 12, 17 and 23. This removal destroys 5 squares of size one, 3 squares of size two, and 1 square of size three. Consequently, the incomplete grid does not have squares of size three, but still has 4 squares of size one and 1 square of size two.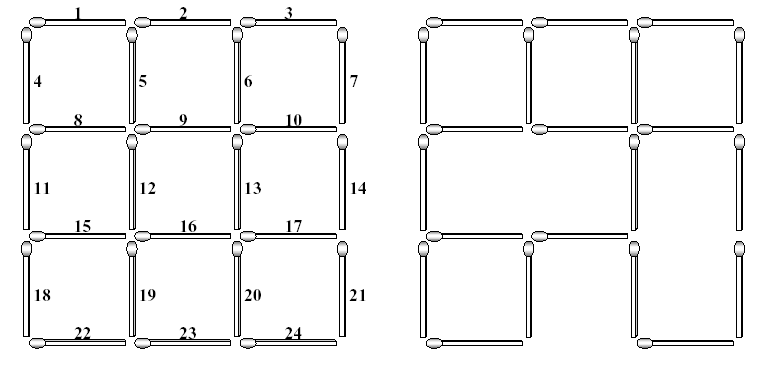 

　　As input, you are given a (complete or incomplete) n*n grid made with no more than 2n(n+1) matchsticks for a natural number 5 <= n . Your task is to compute the minimum number of matchsticks taken 
　　out to destroy all the squares existing in the input n*n grid.

 

　　DLX可重复覆盖的问题，让我们去掉几根火柴，然后把所有的正方形都破坏掉。。。

　　把每一个正方形都当做是一列，然后每一根火柴当做是一行。

 

　　其中对于列和行的构造是麻烦的地方。。。。。。

　　我是枚举每一个正方形，然后枚举这个正方形的每一条边。。。。。。

　　

　　其次就是Link之前要删除掉几行，这里TLE了N次，因为删除的时候要用到row，而且H[r]在某些情况下也应该改变才对（这里忘记了，导致一些数据循环停不下来。。。。。。）

 

代码如下：

#include<iostream>
#include<cstring>

using namespace std;

const int INF=10e8;
const int MaxN=;
const int MaxM=;
const int MaxNode=MaxN*MaxM;

struct DLX
{
    int L[MaxNode],R[MaxNode],U[MaxNode],D[MaxNode],col[MaxNode],row[MaxNode];
    int S[MaxM],H[MaxN];
    int n,m,size;
    int ans;

    void init(int _n,int _m)
    {
        n=_n;
        m=_m;

        for(int i=;i<=m;++i)
        {
            U[i]=D[i]=i;
            R[i]=i+;
            L[i]=i-;
            row[i]=;                // !!!

            S[i]=;
        }

        R[m]=;
        L[]=m;

        size=m;
        ans=INF;

        for(int i=;i<=n;++i)        // !!!
            H[i]=-;
    }

    void Link(int r,int c)
    {
        col[++size]=c;
        ++S[c];
        row[size]=r;

        U[size]=U[c];
        D[size]=c;
        D[U[c]]=size;
        U[c]=size;

        if(H[r]==-)
            H[r]=L[size]=R[size]=size;
        else
        {
            L[size]=L[H[r]];
            R[size]=H[r];
            R[L[H[r]]]=size;
            L[H[r]]=size;
        }
    }

    void remove(int c)
    {
        for(int i=D[c];i!=c;i=D[i])
        {
            R[L[i]]=R[i];
            L[R[i]]=L[i];
        }
    }

    void remove1(int r)
    {
        if(H[r]==-)
            return;

        for(int i=U[H[r]];i!=H[r];i=U[i])
        {
            if(H[row[i]]==i)            // !!!
            {
                if(R[i]==i)
                    H[row[i]]=-;
                else
                    H[row[i]]=R[i];
            }

            L[R[i]]=L[i];
            R[L[i]]=R[i];
        }

        for(int i=R[H[r]];i!=H[r];i=R[i])
            for(int j=U[i];j!=i;j=U[j])
            {
                if(H[row[j]]==j)
                {
                    if(R[j]==j)
                        H[row[j]]=-;
                    else
                        H[row[j]]=R[j];
                }

                L[R[j]]=L[j];
                R[L[j]]=R[j];
            }
    }

    void resume(int c)
    {
        for(int i=U[c];i!=c;i=U[i])
            R[L[i]]=L[R[i]]=i;
    }

    bool vis[MaxM];

    int getH()
    {
        int ret=;

        for(int c=R[];c!=;c=R[c])
            vis[c]=;

        for(int c=R[];c!=;c=R[c])
            if(vis[c])
            {
                ++ret;
                vis[c]=;

                for(int i=D[c];i!=c;i=D[i])
                    for(int j=R[i];j!=i;j=R[j])
                        vis[col[j]]=;
            }

        return ret;
    }

    void Dance(int d)
    {
        if(d+getH()>=ans)
            return;

        if(R[]==)
        {
            if(d<ans)
                ans=d;

            return;
        }

        int c=R[];

        for(int i=R[];i!=;i=R[i])
            if(S[i]<S[c])
                c=i;

        for(int i=D[c];i!=c;i=D[i])
        {
            remove(i);

            for(int j=R[i];j!=i;j=R[j])
                remove(j);

            Dance(d+);

            for(int j=L[i];j!=i;j=L[j])
                resume(j);

            resume(i);
        }
    }
};

int N;
DLX dlx;
int ans1[]={,,,,,};

void slove()
{
    dlx.init(*N*(N+),N*(N+)*(*N+)/);

    int t1,t2;
    int cou=;
    int K,a;

    cin>>K;

    if(K==)
    {
        cout<<ans1[N]<<endl;
        return;
    }

    for(int i=;i<=N;++i)
        for(int j=;j<=(N-i+)*(N-i+);++j)
        {
            ++cou;

            t1=(j-)%(N-i+)++(*N+)*((j-)/(N-i+));

            for(int k=;k<i;++k)
            {
                dlx.Link(k+t1,cou);
                dlx.Link((*N+)*k+t1+i-+N+,cou);
                dlx.Link((*N+)*k+t1+N,cou);
                dlx.Link(k+t1+i*(*N+),cou);
            }
        }

    for(int i=;i<K;++i)
    {
        cin>>a;

        dlx.remove1(a);
    }

    dlx.Dance();

    if(dlx.ans==INF)
        cout<<<<endl;
    else
        cout<<dlx.ans<<endl;
}

int main()
{
    ios::sync_with_stdio(false);

    int T;
    cin>>T;

    while(T--)
    {
        cin>>N;

        slove();
    }

    return ;
}