[每日一题2020.06.11]Codeforces Round #644 (Div. 3) H

A-E见 : 这里

题目

我觉得很有必要把H拿出来单独发( 其实是今天懒得写题了 )

problem H

一个从 1 到 $ 2^m - 1$ 的长度为m的连续二进制序列, 删去指定的n个数, 问剩余的数的中位数是多少

看了题解还琢磨了一个小时才懂, 绝不能跟着题目傻傻的暴力来写

主要的思想还是动态调整的思想

首先比如我们制定m = 3

得到一串序列转换为十进制就是 0 1 2 3 4 5 6 7, 该怎么删才能在不用遍历的情况下找到中位数呢?

( 这题肯定不能暴力, 给定的m = 60, $ 2^{60} = 1152921504606846976 $ )

我们这里用一种动态维护的方式 :

比如n=3, m=3, 删去001, 011, 111

1. 先不管三七二十一, 删去最末尾的那n个数, 判断假设这样删除的话最后的中位数是几

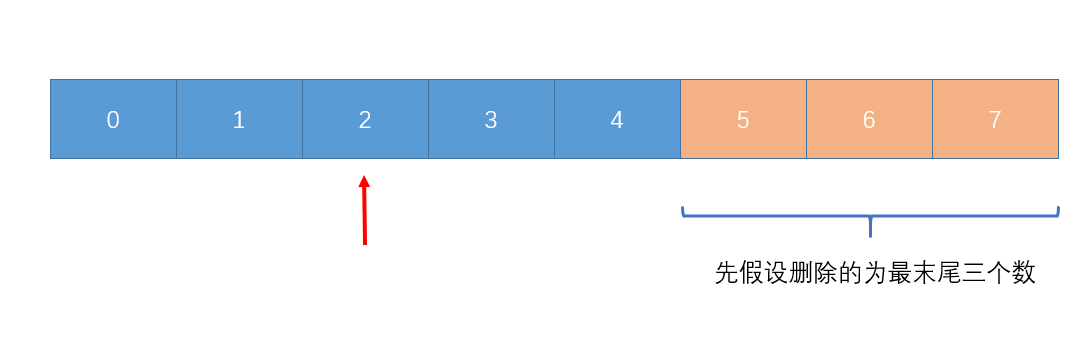
1. 将删除队列从小到大排序, 依次维护调整 比如这里是1, 3, 7
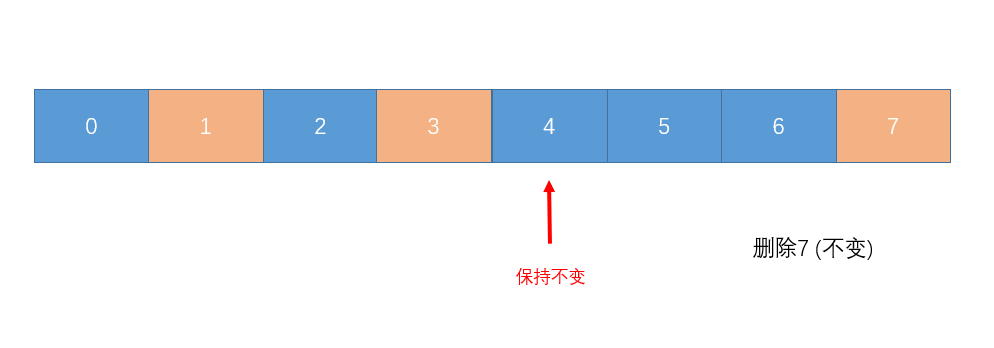
2. 假如删除的为比目前所指向的值大的数, 则不用调整 why ? 见图 :

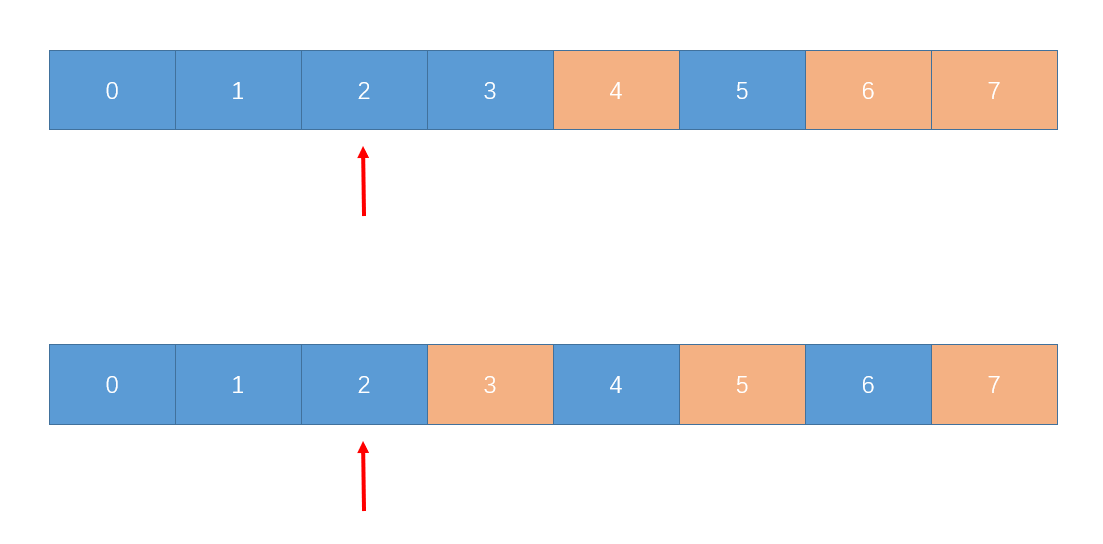
​ 可以看到, 只要删除的数是比目前所指向的大的数, 中位数都是现在这个数, 不用变.

1. 假如删除的为小于或等于目前所指向的值的数, 则指针++ why ? 见图 :

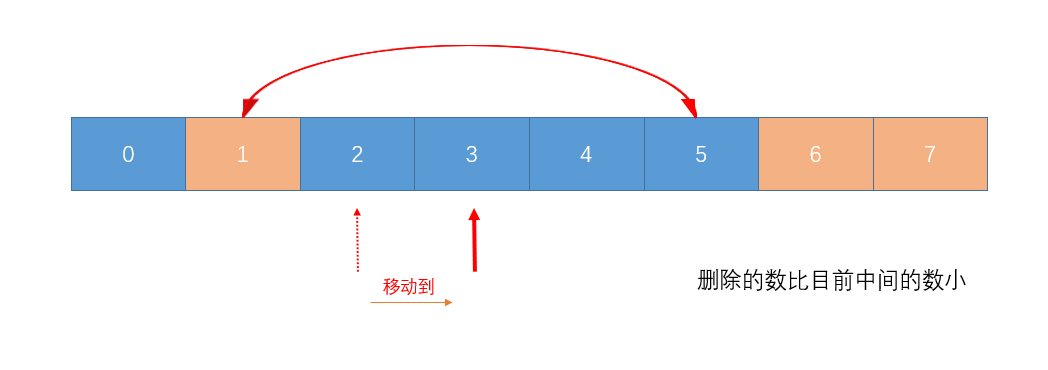
​ 比如我们删除1, 那么相当于原本假设的删除的最后三个数少了一个, 前面增加了一个, 则删除后序列的中间值为现在的值+1 .

​ 我们将3, 7继续删除 :

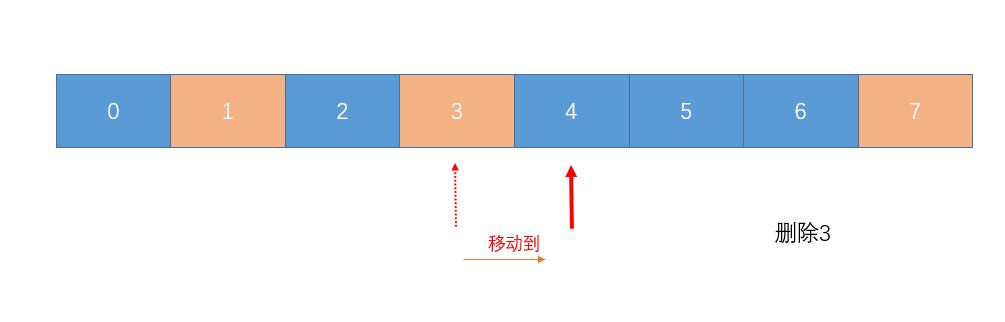
由于原本的值是从0连续的, 所以直接输出最后指针pos的值的二进制形式即为答案.

tips : 见到这种题, 一定要好好想想位置的计算, 很容易出现错误 !

pos的位置 :

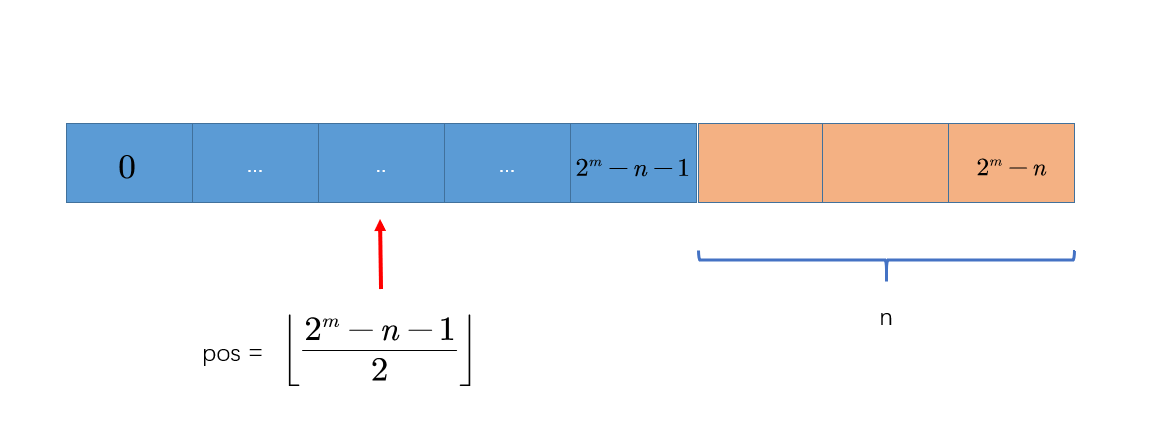
ac代码 :

/*
 * Author: RoccoShi
 * Time: 2020-06-10 20:05:02
*/

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
ll a[105];

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int t;
    cin >> t;
    while(t--) {
    	int n, m;
    	cin >> n >> m;
    	for (int i = 0; i < n; ++i)
    	{
    		string s;
    		cin >> s;
    		ll tmp = 0;
    		for (int j = 0; j < m; ++j)
    		{
    			tmp = tmp*2 + s[j] - '0'; // 二进制 --> 十进制
       		}
       		a[i] = tmp;
    	}
    	sort(a, a + n);
    	ll pos = ((1ll<<m)-1-n) / 2;
    	for (int i = 0; i < n; ++i)
    	{
    		if(a[i] <= pos)
    			pos++;
    	}
    	string ans(m,'0');
    	for(int i = m-1; i >= 0; --i) { // 十进制 --> 二进制
    		ans[i] = (pos & 1) + '0';
    		pos >>= 1;
    	}
    	cout << ans << endl;
    }
    return 0;
}

这里注意下十进制二进制的相互转换代码 ( 建 议 背 诵 ) :

int x = 0;
for (int j = 0; j < m; ++j)
{
    x = x*2 + s[j] - '0'; // 二进制s --> 十进制x
}

for(int i = m-1; i >= 0; --i)
{
    ans[i] = (pos & 1) + '0'; // 十进制 --> 二进制
    pos >>= 1;
}