方格取数（多线程dp，深搜）

https://www.luogu.org/problem/P1004

题目描述

设有N×N的方格图(N≤9)，我们将其中的某些方格中填入正整数，而其他的方格中则放入数字0。如下图所示（见样例）:

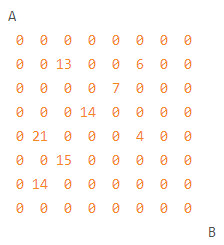
某人从图的左上角的A点出发，可以向下行走，也可以向右走，直到到达右下角的B点。在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字0）。
此人从A点到B点共走两次，试找出2条这样的路径，使得取得的数之和为最大。

输入格式

输入的第一行为一个整数N（表示N×N的方格图），接下来的每行有三个整数，前两个表示位置，第三个数为该位置上所放的数。一行单独的0表示输入结束。

输出格式

只需输出一个整数，表示2条路径上取得的最大的和。

输入输出样例

输入

输出

第一种方法（深搜）：

这道题深搜的最优方法就是两种方案同时从起点出发。因为如果记录完第一种方案，再计算第二种方案，不可控的因素太多了，大多都不是最优解→_→，

但两种方案同时执行就行，因为这可以根据当前的情况来判断最优。

总的来说，每走一步都会有四个分支（你理解成选择或者情况也可以）：

1、两种都向下走

2、第一种向下走，第二种向右走

3、第一种向右走，第二种向下走

4、两种都向右走

每走一步走枚举一下这四种情况，因为在每个点的方案具有唯一性（也就是在某个点走到终点的取数方案只有一个最优解，自己理解一下），所以我们可以开一个数组来记录每一种情况，当重复枚举到一种情况时就直接返回（对，就是剪枝），大大节省了时间（不然会超时哦~）。深搜和DP的时间复杂度时一样的！

 #include <stdio.h>

 #include <string.h>

 #include <iostream>

 #include <string>

 #include <math.h>

 #include <algorithm>

 #include <queue>

 #include <set>

 #include <math.h>

 const int INF=0x3f3f3f3f;

 typedef long long LL;

 const int mod=1e9+;

 const double PI=acos(-);

 const int maxn=1e5+;

 using namespace std;

 int n;

 int A[][];

 int dp[][][][];

 int DFS(int x1,int y1,int x2,int y2)//两种方案同时执行，表示当第一种方案走到x1,y1,第二种方案走到x2,y2时到终点取得的最大数

 {

     if(dp[x1][y1][x2][y2]!=-)//如果这种情况已经被记录过了，直接返回，节省时间

         return dp[x1][y1][x2][y2];

     if(x1==n&&y1==n&&x2==n&&y2==n)//如果两种方案都走到了终点，返回结束

         return ;

     int MAX=;

     //如果两种方案都不在最后一行，就都往下走，统计取得的数，如果有重复，就减去一部分

     if(x1<n&&x2<n)

         MAX=max(MAX,DFS(x1+,y1,x2+,y2)+A[x1+][y1]+A[x2+][y2]-A[x1+][y1]*(x1+==x2+&&y1==y2));

     //如果第一种方案不在最后一行，第二种方案不在最后一列，第一种就向下走，第二种就向右走， 统计取得的数，如果有重复，就减去一部分

     if(x1<n&&y2<n)

         MAX=max(MAX,DFS(x1+,y1,x2,y2+)+A[x1+][y1]+A[x2][y2+]-A[x1+][y1]*(x1+==x2&&y1==y2+));

     //如果第一种方案不在最后一列，第二种方案不在最后一行，第一种就向右走，第二种就向下走， 统计取得的数，如果有重复，就减去一部分

     if(x2<n&&y1<n)

         MAX=max(MAX,DFS(x1,y1+,x2+,y2)+A[x1][y1+]+A[x2+][y2]-A[x1][y1+]*(x1==x2+&&y1+==y2));

     //如果第一种方案和第二种方案都不在最后一列，就都向右走，统计取得的数，如果有重复，就减去一部分

     if(y1<n&&y2<n)

         MAX=max(MAX,DFS(x1,y1+,x2,y2+)+A[x1][y1+]+A[x2][y2+]-A[x1][y1+]*(x1==x2&&y1+==y2+));

     //对最后那个 A[x1][y1+1]*(x1==x2&&y1+1==y2+1))的解释：这个是用来判断两种方案是不是走到了同一格的

     //如果是真，就返回1，否则返回0，如果是1的话，理所当然的可以减去A[x1][y+1]*1,否则减去A[x1][y1+1]*0相当于不减,写得有点精简，省了4个if

     dp[x1][y1][x2][y2]=MAX;//记录这种情况

     return MAX;//返回最大值

 }

 int main()

 {

     scanf("%d",&n);

     //将记录数组初始化成-1，因为可能出现取的数为0的情况，如果直接判断f[x1][y1][x2][y2]!=0（见DFS第一行）

     //可能出现死循环而导致超时，细节问题

     memset(dp,-,sizeof(dp));

     int a,b,c;

     while(~scanf("%d %d %d",&a,&b,&c)&&(a||b||c))//读入

     {

         A[a][b]=c;

     }

     int ans=;

     ans=DFS(,,,)+A[][];//因为DFS中没有考虑第一格，即A[1][1]，所以最后要加一下

     printf("%d\n",ans);

     return ;

 }

第二种方法（DP）：

我们发现题目的数据规模不大，n<=9，所以我们可以考虑用DFS或者DP都可以

这题，是四维动规的模板题，和P1006传纸条基本相似。

我们记f[i][j][k][l]表示第1条路线的i,j走法和第2条路线的k,l走法

显然我们可以两个人一起走，复杂度最多就是9*9*9*9=6561

我们考虑两个人同时走，就相当于数字三角形。

第1条路线只可能是从i-1,j或者i,j-1转移，第2条路线也只可能从k-1,l或者k,l-1转移

而且因为是2个人走，如果走到一点我们的那个点就要打标记说那点上面的值为0

所以我们得到了我们的动归方程（注意：万一i,j与k,l相同这是要小心的！）

状态转移方程为：

dp[i][j][k][l]=max(dp[i-1][j][k-1][l],dp[i-1][j][k][l-1],dp[i][j-1][k-1][l],dp[i][j-1][k][l-1])+A[i][j]+A[k][l];

不过要判断i=k&&j=l的情况。

 #include <stdio.h>

 #include <string.h>

 #include <iostream>

 #include <string>

 #include <math.h>

 #include <algorithm>

 #include <queue>

 #include <set>

 #include <math.h>

 const int INF=0x3f3f3f3f;

 typedef long long LL;

 const int mod=1e9+;

 const double PI=acos(-);

 const int maxn=1e5+;

 using namespace std;

 int n;

 int A[][];

 int dp[][][][];//dp[i][j][k][l]表示两个人同时走，一个走i,j 一个走k,l

 int main()

 {

     scanf("%d",&n);

     int a,b,c;

     while(~scanf("%d %d %d",&a,&b,&c)&&(a||b||c))//读入

     {

         A[a][b]=c;

     }

     for(int i=;i<=n;i++){

         for(int j=;j<=n;j++){

             for(int k=;k<=n;k++){

                 for(int l=;l<=n;l++){

                     dp[i][j][k][l]=max(dp[i-][j][k-][l],max(dp[i][j-][k-][l],max(dp[i-][j][k][l-],dp[i][j-][k][l-])))+A[i][j]+A[k][l];

                     if(i==k&&j==l)

                         dp[i][j][k][l]-=A[i][j];

                 }

             }

         }

     }

     printf("%d\n",dp[n][n][n][n]);

     return ;

 }

思路：

相当于两个人同时走，求最大值，

dp[i][j][x][y]:=第1个人走到坐标(i,j) 第2个人走到坐标(x,y) 时，最大的值

但无论如何，同一时间，1和2走的步数是一样多的，设为p，且i+j-2=p;x+y-2=p

那么dp[i][j][x][y]可以降维为：dp[i][x][p]

那么对于dp[i][x][p]，就有4种情况：dp[i][x][p-1],dp[i-1][x-1][p-1]，dp[i-1][x][p-1]，dp[i][x-1][p-1]

求出最大值再加上a[i][j],a[x][y]

当i==x的时候，显然多加了一次

最后，注意一定要初始化：dp[1][1][0]=a[1][1]，不然会出错

 #include<iostream>

 #include<cstdio>

 #include<algorithm>

 #include<string>

 #include<cstring>

 #include<queue>

 #include<stack>

 #include<cmath>

 #include<set>

 #include<map>

 #include<functional>

 using namespace std;

 #define ll long long

 typedef pair<ll,int>P;

 const ll INF=1e17+;

 const int N=,mod=1e9+;

 int a[N][N];

 int dp[N][N][*N];

 int main(){

     int n;

     scanf("%d",&n);

     int x,y,k;

     while(scanf("%d%d%d",&x,&y,&k)&&x+y+k!=){

         a[x][y]=k;

     }

     dp[][][]=a[][];

     for(int p=;p<=*n-;p++){//步数

         for(int i=;i<=n;i++){

             for(int x=;x<=n;x++){

                 int j=p+-i,y=p+-x;

                 int tmp=max(dp[i][x][p-],dp[i-][x-][p-]);

                 tmp=max(tmp,dp[i-][x][p-]);

                 tmp=max(tmp,dp[i][x-][p-]);

                 dp[i][x][p]=tmp+a[i][j]+a[x][y];

                 if(i==x)dp[i][x][p]-=a[x][y];

             }

         }

     }

     printf("%d\n",dp[n][n][*n-]);

 }

下面粘出洛谷大佬以墨的题解：

这题和传纸条很像

一级

显然，用f[i][j][k][l]表示第一个人走到(i,j)，第二个人走到(k,l)的最优解，因为楼下讲了太多，我就不再赘述了。发个代码。

 #include<cstdio>

 #include<algorithm>

 using namespace std;

 struct point

 {

     int x,y,data;

 }p[];

 int n,m,map[][],f[][][][];

 int main()

 {

     int i,j,k,l;

     scanf("%d",&n);

     while()

     {

         int a,b,c;

         scanf("%d%d%d",&a,&b,&c);

         if(!a&&!b&&!c)

             break;

         p[++m].x=a;

         p[m].y=b;

         p[m].data=c;

     }

     for(i=;i<=m;i++)

         map[p[i].x][p[i].y]=p[i].data;

     for(i=;i<=n;i++)

         for(j=;j<=n;j++)

             for(k=;k<=n;k++)

             {

                 l=i+j-k;

                 if(l<=)

                     break;

                 f[i][j][k][l]=max(f[i-][j][k-][l],max(f[i-][j][k][l-],max(f[i][j-][k-][l],f[i][j-][k][l-])));

                 if(i==k&&j==l)

                     f[i][j][k][l]+=map[i][j];

                 else

                     f[i][j][k][l]+=map[i][j]+map[k][l];

             }

     printf("%d\n",f[n][n][n][n]);

     return ;

 }

二级

然而这题数据太弱，范围这么小偶也没想到，但是钻研的精神很可贵，还是要多想想。

像楼下说的，用三维数组，优化空间。可以用路径长度代表阶段

f(l,i,ii)表示当前路径长度为l（也就是说当前是第l个状态），第一个人走到(i,l-i)的位置，第二个人走到(ii,l-ii)的位置。

具体原因楼下同样讲得太多了，因为后面还有料，现在就不多说了。

三级

看过楼下题解的同学应该能够发现，每一次的状态转移都只和上一个阶段有关，即第l-1个阶段。

所以说可以用滚动数组，只记录当前阶段和2的余数的阶段即可。

若l%2==0，则上一个状态l%2==1。反之亦然。

这样空间复杂度从O(n^4)->O(n^3)->O(2n^2)

四级

其实这样已经差不多了，但是还可以继续优化。

如果对01背包的以为写法非常熟悉的话......

可以模仿，枚举i和ii的时候，如果倒着做，那么当前的值就是上一个阶段的值，连滚动数组都不用。

空间复杂度再降到O(n^2)

贴上四级的代码~~~

 #include<cstdio>

 #include<algorithm>

 using namespace std;

 struct point

 {

     int x,y,data;//记录每个点的位置和数值

 }p[];

 int n,m,map[][],f[][];

 int main()

 {

     int i,ii,j,jj,l;

     scanf("%d",&n);

     while()

     {

         int a,b,c;

         scanf("%d%d%d",&a,&b,&c);

         if(!a&&!b&&!c)

             break;

         p[++m].x=a;

         p[m].y=b;

         p[m].data=c;

     }

     for(i=;i<=m;i++)

         map[p[i].x][p[i].y]=p[i].data;

     for(l=;l<=n*;l++)//每个点最少横着竖着都走一格，最多都走n格就到终点

         for(i=l-;i>=;i--)//和前面说的一样，倒着做

             for(ii=l-;ii>=;ii--)

             {

                 j=l-i;jj=l-ii;//i+j=ii+jj=l

                 f[i][ii]=max(max(f[i][ii],f[i-][ii-]),max(f[i-][ii],f[i][ii-]))+map[i][j];

 //重点说明一下吧，这里省略了很多。如果i不减1，意思就是j-1，因为上一个阶段就是l-1嘛。如果ii-1，意思就是说jj不减1。

                 f[i][ii]+=map[ii][jj]*(i!=ii);

 //如果i==ii，其实就是(i==ii&&j==jj)，因为和都是l嘛。如果走过一遍，第二遍走得到的值就是0（题目上说的）。

             }

     printf("%d\n",f[n][n]);

 //输出意思是在路径长度为2*n的阶段，两遍都走到(n,n)的最优值。因为在这里(j=2*n-i=n,jj=2*n-ii=n),所以走到的就是(n,n)的位置

     return ;

 }

OVER ! 一个小小的建议，如果你想对这种两边一起做的DP有更深入的了解，可以做：传纸条和回文的路径

后者很难！！！

第三种方法（费用流，SPFA）：

（蒟蒻表示暂时不会，先粘大佬的代码，以后再看）

SPFA

简要介绍一下如何构图

拆点：因为每个方格只取一次，但要走两遍，因此我们考虑对于矩阵中每个方格拆为两个节点，一个为流入点，记为i；一个为流出点，记为i'。连两条边从i->i’，两条容量都为1，费用为-g[i][j]和0。
编号：这个大家有各自的习惯。我的题解中具体看我程序中的hashin和hashout函数和注释，hashin用于编号我前文所提到的i，hashout用于编号我前文所提到的i'。
连接节点：每个节点的out连接它的右边和它下边节点的流入点，对于边界特殊处理一下，s连(0,0)的入点，(n-1,n-1)连t点。

这样构图跑一遍spfa的最小费用最大流就OK了。

 #include <cstdio>

 #include <cstring>

 #include <queue>

 #define INF 0x7f7f7f7f

 using namespace std;

 struct Edge{

     int u;//大多数算法在邻接表中并不需要这个，但费用流比较例外

     int v;

     int f;//残量

     int c;//费用

     int next;

 }e[];//网络流的题目都要记得边数开两倍，因为还有反向弧

 int head[];

 int n,m,s,t;

 int ecnt = ;

 inline void AddEdge(int _u,int _v,int _f,int _c) {

     e[ecnt].next = head[_u];

     head[_u] = ecnt;

     e[ecnt].u = _u;

     e[ecnt].v = _v;

     e[ecnt].f = _f;

     e[ecnt].c = _c;

     ecnt++;

 }

 inline void Add(int _u,int _v,int _f,int _c) {

     AddEdge(_u,_v,_f,_c);

     AddEdge(_v,_u,,-_c);

 }

 int dis[];

 bool inq[];

 int pre[];

 bool SPFA() {

     queue <int> q;

     q.push(s);

     memset(dis,0x7f,sizeof(dis));

     memset(inq,,sizeof(inq));

     memset(pre,-,sizeof(pre));

     inq[s] = true;

     dis[s] = ;

     while (!q.empty()) {

         int cur = q.front();

         q.pop();

         inq[cur] = false;

         for (int i = head[cur];i != -;i = e[i].next) {

             if (e[i].f !=  && dis[e[i].v] > dis[cur] + e[i].c) {

                 dis[e[i].v] = dis[cur] + e[i].c;

                 pre[e[i].v] = i;

                 if (!inq[e[i].v]) {

                     inq[e[i].v] = true;

                     q.push(e[i].v);

                 }

             }

         }

     }

     return dis[t] != INF;

 }

 void MICMAF(int &flow,int &cost) {

     flow = ;

     cost = ;

     while (SPFA()) {

         int minF = INF;

         for (int i=pre[t];i != -;i=pre[e[i].u]) minF = min(minF,e[i].f);

         flow += minF;

         for (int i=pre[t];i != -;i=pre[e[i].u]) {

             e[i].f -= minF;

             e[i^].f += minF;

         }

         cost += dis[t] * minF;

     }

 }

 /*

 节点编号规则：

 源点：0

 矩阵节点(入)：n*x+y+1

 矩阵节点(出)：n*n+n*x+y+1

 汇点：2*n*n+1

 */

 int g[][];

 inline int hashin(int x,int y) {

     return n*x+y+;

 }

 inline int hashout(int x,int y) {

     return n*n + n * x + y + ;

 }

 int main() {

     memset(head,-,sizeof(head));

     scanf("%d",&n);

     int x,y,v;

     while (scanf("%d%d%d",&x,&y,&v) == ) {

         if (x ==  && y ==  && v == ) break;

         x --;

         y --;

         g[x][y] = v;

     }

     s = ;

     t =  * n * n + ;

     Add(s,,,);

     Add(*n*n,t,,);

     for (int i=;i<n;i++)

         for (int j=;j<n;j++) {

             int in = hashin(i,j);

             int out = hashout(i,j);

             Add(in,out,,);//邻接表中后插入的先遍历，卡常，f=1是因为只可能再经过一次

             Add(in,out,,-g[i][j]);

             if (i != n - ) Add(out,hashin(i+,j),,);

             if (j != n - ) Add(out,hashin(i,j+),,);

         }

     int f,c;

     MICMAF(f,c);

     printf("%d\n",-c);

     return ;

 }