题解 P5663 【加工零件【民间数据】】

博客园体验更佳

讲讲我的做法

确定做法

首先，看到这道题，我直接想到的是递归，于是复杂度就上天了，考虑最短路。

如何用最短路

首先，看一张图

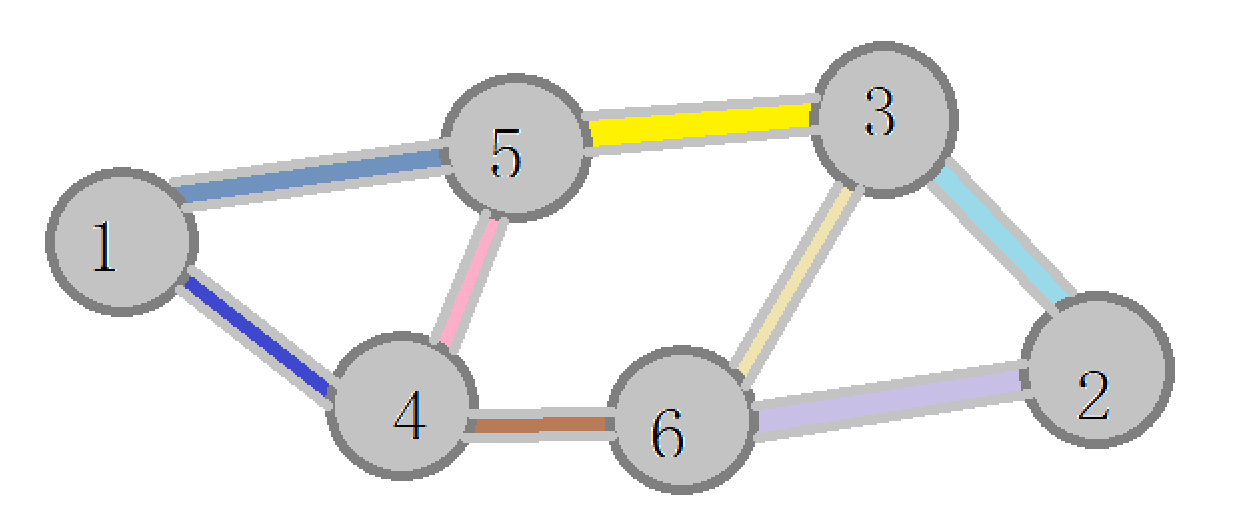
我们该如何解决问题？

问题:\(3\)做\(5\)阶段的零件\(1\)要不要做呢？

其实，实质就是看\(3\)到\(1\)有没有长度为\(5\)的路径。

问题:\(3\)做\(7\)阶段的零件\(1\)要不要做呢？

其实，实质就是看\(3\)到\(1\)有没有长度为\(7\)的路径。

问题:\(3\)做\(6\)阶段的零件\(1\)要不要做呢？

其实，实质就是看\(3\)到\(1\)有没有长度为\(6\)的路径。

仔细思考这\(3\)个问题，我们会发现，如果\(3\)到\(1\)有长度为\(5\)的路径，那么\(3\)到\(1\)一定有长度为\(7\)的路径，但并不一定有长度为\(6\)的路径。

所以，我们要对每个点求一遍奇数路径，和偶数路径。

实现最短路

最短路的算法有很多，这道题最好用\(dijkstra\)，或\(bfs\)。

这道题的时限并不紧，并且\(dijkstra\)细节太多，我就来演示\(bfs\)实现的最短路

void bfw(){//我有一个好朋友叫bfw，所以我写bfs时，喜欢把函数名起为bfw
	memset(ji,0x3f,sizeof(ji));//奇数最短路径
	memset(ou,0x3f,sizeof(ou));//偶数最短路径
	queue<pair<int,int> >q;
	q.push(make_pair(1,0));
    ou[1]=0;
	while(q.size()){
		int x=q.front().first,y=q.front().second;
		for(int i=0;i<v[x].size();i++){
			if(y%2==1){//奇数+1=偶数
				if(y+1<ou[v[x][i]]){
					ou[v[x][i]]=y+1;//更新答案
					q.push(make_pair(v[x][i],y+1));
				}
			}else{//偶数+1=奇数
				if(y+1<ji[v[x][i]]){
					ji[v[x][i]]=y+1;//更新答案
					q.push(make_pair(v[x][i],y+1));
				}
			}
		}
		q.pop();
	}
}

\(v\)数组是一个动态数组，也就是\(vector\)，曹老师教我们多用\(STL\)写程序

如果你写这样的\(bfs\)民间数据会\(WA\) \(1\)个点 ，这个点是这样的

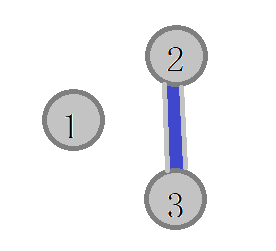
\(1\)号点是一个孤点，没有偶数路径，所以，我们的\(bfs\)要这么写

void bfw(){//我有一个好朋友叫bfw，所以我写bfs时，喜欢把函数名起为bfw
	memset(ji,0x3f,sizeof(ji));//奇数最短路径
	memset(ou,0x3f,sizeof(ou));//偶数最短路径
	queue<pair<int,int> >q;
	for(int i=0;i<v[1].size();i++){
		ji[v[1][i]]=1;
		q.push(make_pair(v[1][i],1));
	}
	while(q.size()){
		int x=q.front().first,y=q.front().second;
		for(int i=0;i<v[x].size();i++){
			if(y%2==1){//奇数+1=偶数
				if(y+1<ou[v[x][i]]){
					ou[v[x][i]]=y+1;//更新答案
					q.push(make_pair(v[x][i],y+1));
				}
			}else{//偶数+1=奇数
				if(y+1<ji[v[x][i]]){
					ji[v[x][i]]=y+1;//更新答案
					q.push(make_pair(v[x][i],y+1));
				}
			}
		}
		q.pop();
	}
}

简要讲解主程序

有了这些主程序应该是很简单的了

int main(){
	int n,m,q;
	read(n);read(m);read(q);
	for(int i=1;i<=m;i++){
		int x,y;
		read(x);read(y);//无向边
		v[x].push_back(y);//连边
		v[y].push_back(x);//连边
	}
	bfw();//跑最短路
	while(q--){
		int x,y;
		read(x);read(y);
		if(y%2==0){
			if(ou[x]>y)puts("No");//如果大于就不可能了
			else puts("Yes");
		}else{
			if(ji[x]>y)puts("No");//如果大于就不可能了
			else puts("Yes");
		}
	}
	return 0;
}

总结

先来看一看这题完整的代码了

#include <bits/stdc++.h>
using namespace std;
template<typename T>inline void read(T &FF){
	T RR=1;FF=0;char CH=getchar();
	for(;!isdigit(CH);CH=getchar())if(CH=='-')RR=-1;
	for(;isdigit(CH);CH=getchar())FF=(FF<<1)+(FF<<3)+(CH^48);
	FF*=RR;
}
template<typename T>void write(T x){
	if(x<0)putchar('-'),x*=-1;
	if(x>9)write(x/10);
	putchar(x%10+48);
}
vector<int>v[100010];
int ji[100010],ou[100010];
void bfw(){//我有一个好朋友叫bfw，所以我写bfs时，喜欢把函数名起为bfw
	memset(ji,0x3f,sizeof(ji));//奇数最短路径
	memset(ou,0x3f,sizeof(ou));//偶数最短路径
	queue<pair<int,int> >q;
	for(int i=0;i<v[1].size();i++){
		ji[v[1][i]]=1;
		q.push(make_pair(v[1][i],1));
	}
	while(q.size()){
		int x=q.front().first,y=q.front().second;
		for(int i=0;i<v[x].size();i++){
			if(y%2==1){//奇数+1=偶数
				if(y+1<ou[v[x][i]]){
					ou[v[x][i]]=y+1;//更新答案
					q.push(make_pair(v[x][i],y+1));
				}
			}else{//偶数+1=奇数
				if(y+1<ji[v[x][i]]){
					ji[v[x][i]]=y+1;//更新答案
					q.push(make_pair(v[x][i],y+1));
				}
			}
		}
		q.pop();
	}
}
int main(){
	int n,m,q;
	read(n);read(m);read(q);
	for(int i=1;i<=m;i++){
		int x,y;
		read(x);read(y);//无向边
		v[x].push_back(y);//连边
		v[y].push_back(x);//连边
	}
	bfw();//跑最短路
	while(q--){
		int x,y;
		read(x);read(y);
		if(y%2==0){
			if(ou[x]>y)puts("No");//如果大于就不可能了
			else puts("Yes");
		}else{
			if(ji[x]>y)puts("No");//如果大于就不可能了
			else puts("Yes");
		}
	}
	return 0;
}

这道题还是比较有思维含量的，民间数据也出的很好，让我们思考全面。

最后，还是希望大家不懂就在评论区问，觉得好就点赞！