Java实现背包问题

1 问题描述

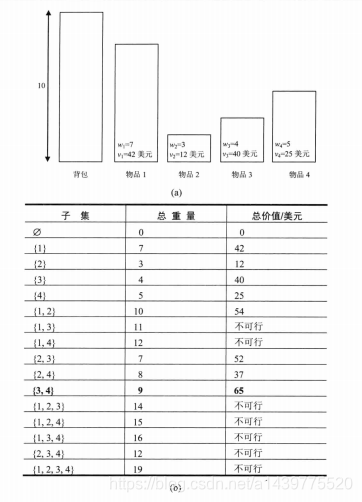
给定n个重量为w1，w2，w3，…，wn，价值为v1，v2，…，vn的物品和一个承重为W的背包，求这些物品中最有价值的子集（PS：每一个物品要么选一次，要么不选），并且要能够装到背包。

附形象描述：就像一个小偷打算把最有价值的赃物装入他的背包一样，但如果大家不喜欢扮演小偷的角色，也可以想象为一架运输机打算把最有价值的物品运输到外地，同时这些物品的重量不能超出它的运输能力。

2 解决方案

2.1 蛮力法

使用蛮力法解决包含n个物品的背包问题，首先得求出这n个物品的所有子集，对于每一个物品存在两种情况：选中（在程序中用1表示），未选中（在程序中用0表示）。该n个物品的所有子集数数量为2^n。下面请看一个简单示例：

package com.liuzhen.chapterThree;

public class Knapsack {

    public int maxSumValue = 0;        //定义满足背包问题子集的最大承重所得的总价值，初始化为0
    /*
     * 数组A的行数为2^n，代表n个物品共有2^n个子集，列数为n。即每一行的排列为一个背包实例
     * 数组weight存放每个物品的具体重量
     * 数组value存放每个物品的具体价值
     * n代表共有n个物品
     * maxWeight表示背包最大承重量
     */
    public void bruteForce(int[][] A,int[] weight,int[] value,int n,int maxWeight){

        for(int i = 0;i < Math.pow(2, n);i++){  //总共有2^n个子集，需要进行2^n次循环，及数组A有2^n行
            int temp1 = i;
            for(int j = 0;j < n;j++){    //数组A有n列，每一列代表一个物品
                int temp2 = temp1%2;
                A[i][j] = temp2;
                temp1 = temp1/2;
            }
        }

        printArray(A,weight,value,maxWeight);

    }

    //输出穷举方案的背包实例的选择物品（0代表不包含该物品，1表示包含该物品）的总重量及总价值，并输出最优实例的总价值
    public void printArray(int[][] A,int[] weight,int[] value,int maxWeight){
        int len1 = A.length;         //二维数组的行数
        int len2 = A[0].length;      //二维数组的列数
        for(int i = 0;i < len1;i++){
            int tempWeight = 0;      //暂时计算当前选中背包实例物品的总重量，初始化为0
            int tempSumValue = 0;    //暂时计算当前选中背包实例物品的总价值，初始化为0
            for(int j = 0;j < len2;j++){
                System.out.print(A[i][j]+" ");
//                if(A[i][j] != 0)
//                    System.out.print(" 物品"+j);
                tempWeight += A[i][j]*weight[j];
                tempSumValue += A[i][j]*value[j];
            }
            System.out.print("\t"+"总重量为："+tempWeight);
            if(tempWeight <= maxWeight)
                System.out.print("\t"+"总价值为："+tempSumValue);
            else
                System.out.print("\t"+"不可行（超出背包最大承重）");
            if(tempWeight <= maxWeight && tempSumValue > maxSumValue)
                maxSumValue = tempSumValue;
            System.out.println();
        }
        System.out.println("穷举查找得知，最优解的总价值为："+maxSumValue);
    }

    public static void main(String[] args){
        Knapsack test = new Knapsack();
        int[][] A = new int[16][4];
        int[] weight = {7,3,4,5};
        int[] value = {42,12,40,25};
        test.bruteForce(A,weight,value,4,10);      //背包的承重最大为10
    }

}

运行结果：

0 0 0     总重量为：0    总价值为：0
0 0 0     总重量为：7    总价值为：42
1 0 0     总重量为：3    总价值为：12
1 0 0     总重量为：10    总价值为：54
0 1 0     总重量为：4    总价值为：40
0 1 0     总重量为：11    不可行（超出背包最大承重）
1 1 0     总重量为：7    总价值为：52
1 1 0     总重量为：14    不可行（超出背包最大承重）
0 0 1     总重量为：5    总价值为：25
0 0 1     总重量为：12    不可行（超出背包最大承重）
1 0 1     总重量为：8    总价值为：37
1 0 1     总重量为：15    不可行（超出背包最大承重）
0 1 1     总重量为：9    总价值为：65
0 1 1     总重量为：16    不可行（超出背包最大承重）
1 1 1     总重量为：12    不可行（超出背包最大承重）
1 1 1     总重量为：19    不可行（超出背包最大承重）
穷举查找得知，最优解的总价值为：65

2.2 减治法

2.2.1 递归求解

背包问题的实质是求取n个不同物品的所有子集，在此基础上寻找重量合适，总价值最大的子集。此处只给出如何求出n个不同物品的所有子集实现，至于如何寻找符合背包问题的子集，感兴趣的同学可以自己动手实现以下哟~

此处是运用减治法思想，根据二进制反射格雷码的算法思想，来实现此问题。具体解释，请看下面一段出自《算法设计与分析基础》第三版上讲解：

package com.liuzhen.chapter4;

import java.util.LinkedList;
import java.util.List;

public class GrayCode {
    //递归求取n个不同物品的所有子集
    public String[] getGrayCode2(int n){
        int len = (int) Math.pow(2, n);
        String[] result = new String[len];
        if(n == 1){
            result[0] = "0";
            result[1] = "1";
            return result;
        }
        String[] temp = getGrayCode2(n-1);               //递归求取n-1个不同物品的所有子集
        for(int i = 0;i < temp.length;i++){        //根据格雷码去掉最高位,前一半和后一半二进制数完全一样的对称性
            result[i] = "0" + temp[i];         //前一半格雷码，最高位为0
            result[result.length-1-i] = "1" + temp[i];   //后一半格雷码，最高位为1
        }
        return result;
    }

    public static void main(String[] args){
        GrayCode test = new GrayCode();
        String[] temp2 = test.getGrayCode2(3);
        System.out.println("使用递归求解n个物品所有子集结果如下：");
        for(int i = 0;i < temp2.length;i++)
            System.out.println(temp2[i]);
    }
}

运行结果：

使用递归求解n个物品所有子集结果如下：
001
010
111
100

2.2.2 非递归求解（运用异或运算）

此处也使用求取格雷码的思想，完成求取n个物品的所有子集，不过此处是使用非递归来实现，运用异或运算，其构造非常巧妙，个人感觉要理解这种编码方式和思想得多多运用，直至熟能生巧。

package com.liuzhen.chapter4;

import java.util.LinkedList;
import java.util.List;

public class GrayCode {
    //运用异或运算得到n个不同物品的所有子集
    public List<Integer> getGaryCode1(int n){
        List<Integer> result = new LinkedList<>();
        if(n >= 0){
            result.add(0);
            int top = 1;
            for(int i = 0;i < n;i++){
                System.out.print("result.size() = "+result.size()+"  ");
                for(int j = result.size()-1;j >= 0;j--){
                    System.out.print("result.get("+j+")^top = "+result.get(j)+"^"+top+" = "+(result.get(j)^top)+"  ");
                    result.add(result.get(j)^top);   //符号‘^’是异或运算（使用具体数字的二进制进行运算），即1^0=1,0^1=1,0^0=0,1^1=0
                }
                System.out.println();
                top <<= 1;         //top二进制左移1位，相当于top=top*2
                System.out.println("top = "+top);
            }
        }
        return result;
    }
    //把十进制数转换成长度为n的二进制数
    public StringBuffer[] getBinary(List<Integer> A,int n){
        StringBuffer[] result = new StringBuffer[A.size()];
        for(int i = 0;i < A.size();i++){
            int temp1 = A.get(i);
            int judge = n;
            char[] temp2 = new char[n];     //用于存放temp1的n位二进制数
            while(judge > 0){
                int temp3 = temp1%2;
                temp2[judge-1] = (char) (temp3+48);  //对照char的unicode编码，把int型数字转换为char型
                temp1 = temp1/2;
                judge--;
            }
            result[i] = new StringBuffer(String.valueOf(temp2));
        }
        return result;
    }

    public static void main(String[] args){
        GrayCode test = new GrayCode();
        List<Integer> temp = test.getGaryCode1(3);
        System.out.println(temp);
        StringBuffer[] temp1 = test.getBinary(temp, 3);
        for(int i = 0;i < temp1.length;i++)
            System.out.println(temp1[i]);
    }
}

运行结果：

result.size() = 1  result.get(0)^top = 0^1 = 1
top = 2
result.size() = 2  result.get(1)^top = 1^2 = 3  result.get(0)^top = 0^2 = 2
top = 4
result.size() = 4  result.get(3)^top = 2^4 = 6  result.get(2)^top = 3^4 = 7  result.get(1)^top = 1^4 = 5  result.get(0)^top = 0^4 = 4
top = 8
[0, 1, 3, 2, 6, 7, 5, 4]
001
010
111
100

2.3 动态规划法

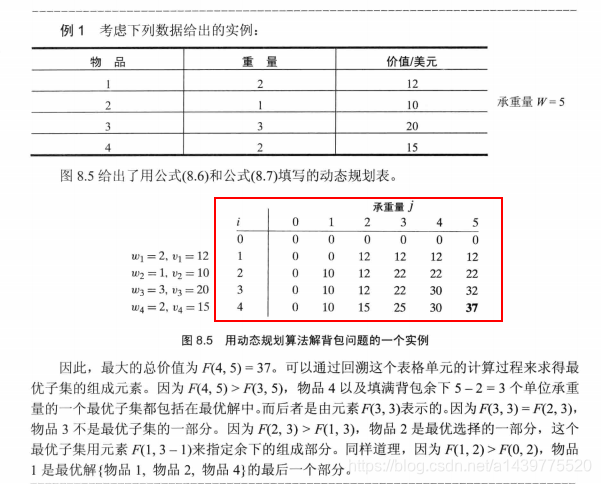
此处编码思想主要参考自《算法设计与分析基础》第三版的一段讲解，具体如下：

package com.liuzhen.chapter8;

public class MFKnapsack {
    /*
     * 参数weight:物品1到物品n的重量，其中weight[0] = 0
     * 参数value:物品1到物品n的价值，其中value[0] = 0
     * 函功能：返回背包重量从0到所有物品重量之和区间的每一个重量所能达到的最大价值
     */
    public int[][] getMaxValue(int[] weight, int[] value) {
        int lenRow = weight.length;
        int lenColumn = 0;
        for(int i = 0;i < weight.length;i++)
            lenColumn += weight[i];
        int[][] F = new int[lenRow][lenColumn+1]; //列值长度加1，是因为最后一列要保证重量值为lenColumn
        for(int i = 1;i < weight.length;i++) {
            for(int j = 1;j <= lenColumn;j++) {
                if(j < weight[i])
                    F[i][j] = F[i-1][j];
                else {
                    if(F[i-1][j] > F[i-1][j-weight[i]] + value[i])
                        F[i][j] = F[i-1][j];
                    else
                        F[i][j] = F[i-1][j-weight[i]] + value[i];
                }
            }
        }
        return F;
    }

    public static void main(String[] args) {
        MFKnapsack test = new MFKnapsack();
        int[] weight = {0,2,1,3,2};
        int[] value = {0,12,10,20,15};
        int[][] F = test.getMaxValue(weight, value);
        System.out.println("背包承重从0到所有物品重量之和为8的承重能够达到的最大价值分别为：");
        for(int i = 0;i < F.length;i++) {
            for(int j = 0;j < F[0].length;j++)
                System.out.print(F[i][j]+"\t");
            System.out.println();
        }
    }
}

运行结果：

背包承重从0到所有物品重量之和为8的承重能够达到的最大价值分别为：
   0    0    0    0    0    0    0    0
   0    12    12    12    12    12    12    12
   10    12    22    22    22    22    22    22
   10    12    22    30    32    42    42    42
   10    15    25    30    37    45    47    57