AI之旅（5）：正则化与牛顿方法

前置知识

  导数，矩阵的逆

知识地图

  正则化是通过为参数支付代价的方式，降低系统复杂度的方法。牛顿方法是一种适用于逻辑回归的求解方法，相比梯度上升法具有迭代次数少，消耗资源多的特点。

过拟合与欠拟合

  回顾线性回归和逻辑回归这两个算法，我们发现特征这个词汇在频繁出现。特征是从不同的角度对事物进行描述，特征数量会决定模型的复杂程度和最终的性能表现。

  为了方便讨论，我们通过添加高阶多项式的方法来增加特征数量。原始数据集中只有一个特征，依次添加原始特征的2次方，3次方......直至6次方作为新的特征。

  当特征数量不足时会使得模型太简单，模型不能很好地拟合样本。这种情况称为欠拟合，如下图所示：

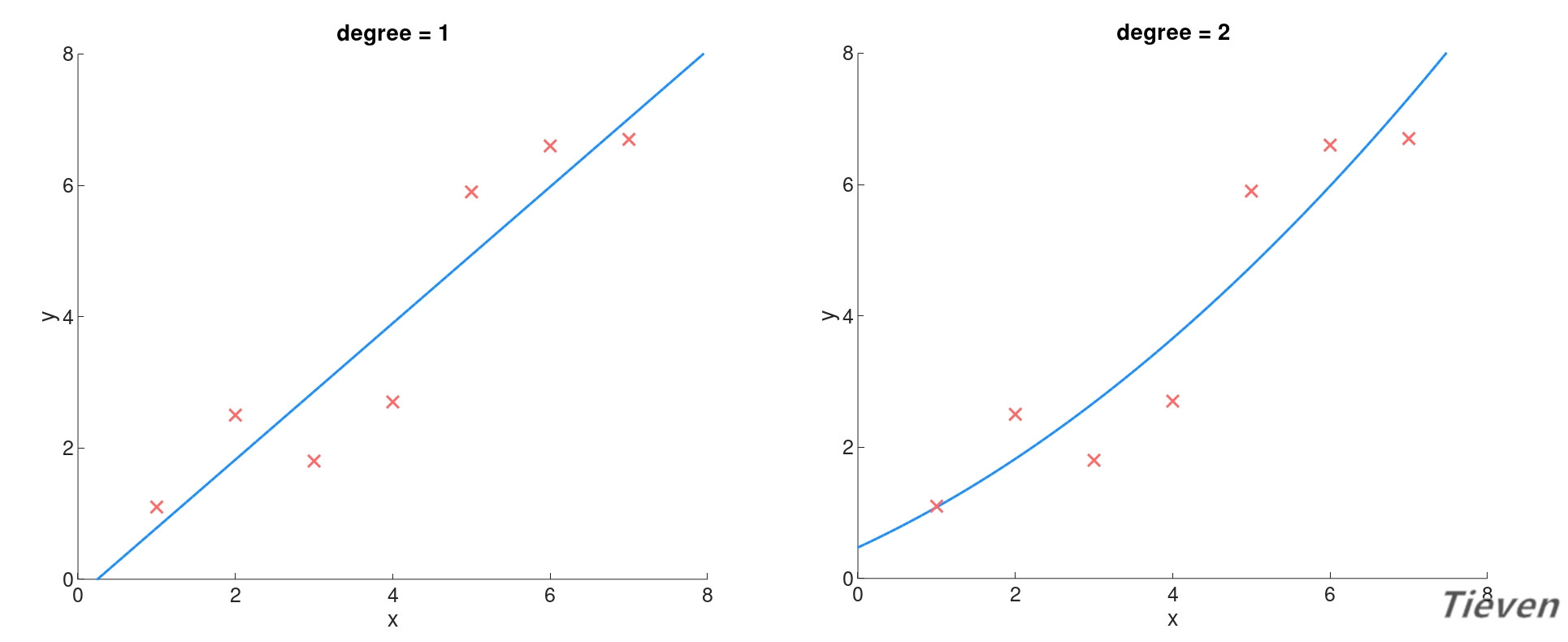
  随着特征数量的增加，模型的复杂度也逐渐增加，模型对样本的拟合程度也在逐步提升，如下图所示：

  当特征数量过多时会使得模型太复杂，模型可以极好地拟合样本。这种情况称为过拟合，如下图所示：

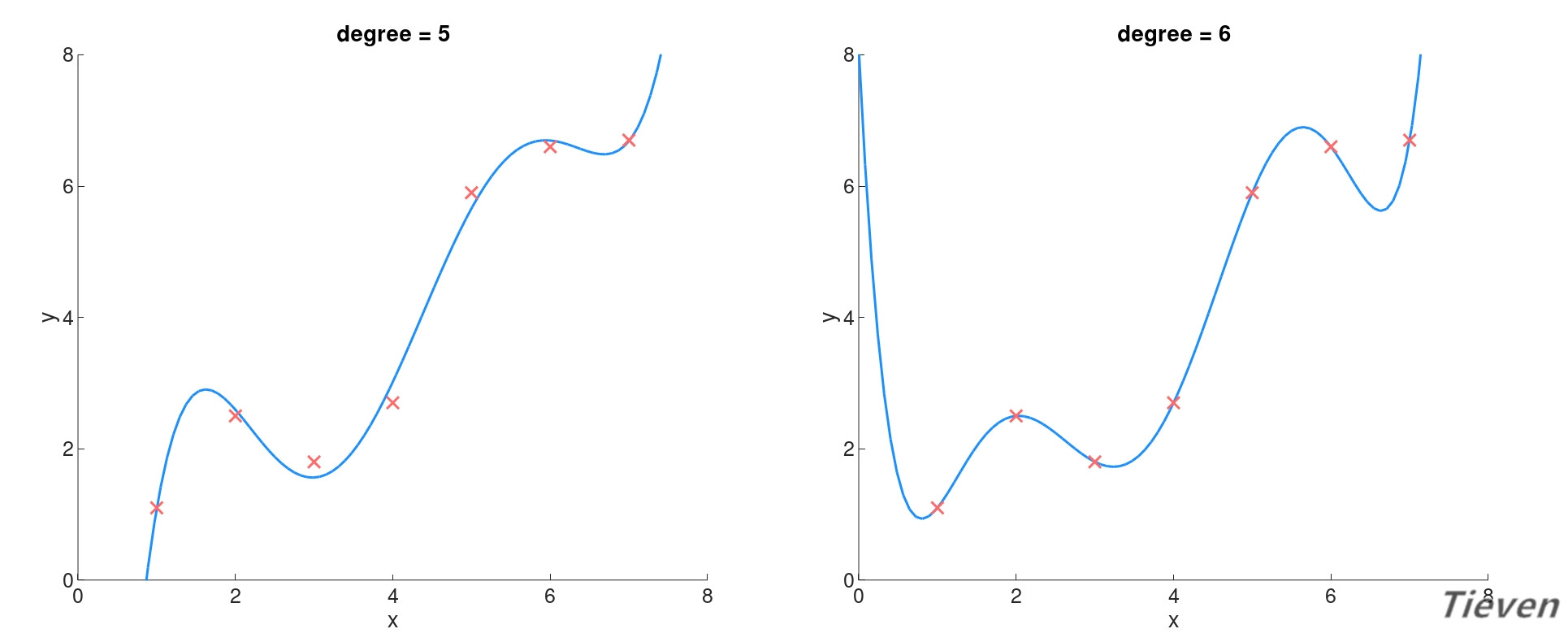
  显然欠拟合的情况是不好的，那么过拟合的情况如何呢？虽然模型很好地拟合了数据集，然而这不是一个好的模型，它对数据集过度拟合以至于对新样本的泛化能力很差。

  “如无必要，勿增实体”。参数是特征的权重，当参数越大时特征的影响越大，当参数越小时特征的影响越小。如果能让参数尽量变小，就可以降低模型的复杂度。

  为了避免出现过拟合的情况，可以在代价函数中加入正则化项，正则化项是关于参数的代价。因为存在代价，算法在寻找全局最优点的过程中，必须使得参数尽量最小化。

正则化

  线性回归原代价函数如下：

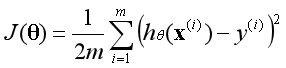
  线性回归新代价函数如下：

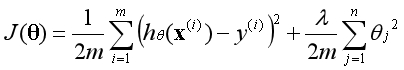
  λ称为正则化参数，和学习率α一样，这是一个需要手动调节的参数。正则化参数λ的作用是调节以下两个目标间的平衡关系：

  目标一：使模型更好地拟合数据；

  目标二：使参数θ尽量最小化；

  当正则化参数λ减小时，需要为参数θ支付的代价变小，模型的复杂度提高，存在的风险是可能会出现过拟合。

  当正则化参数λ增大时，需要为参数θ支付的代价变大，模型的复杂度降低，存在的风险是可能会出现欠拟合。

  注：1/2是为了后续求导的方便；

  正则化项的含义是，平均每个样本需要为参数支付的代价，代价以参数平方的形式体现。数据集中原本有n个特征，加入一列全为1的常数项后一共有n+1个特征，对应n+1个参数。

  下图为特征相同的情况下，当正则项参数不同时模型的变化。随着正则项参数增大，需要为参数所支付的代价增大。为了最小化代价函数，必须降低特征的权重，进而简化了模型。

  以下为对应的参数：

  注意j是从1开始算起的，也就是说，常数项对应的参数θ0不参与正则化。这是理解和实践中很容易混淆的地方，下面用对比图说明这样约定的原因。

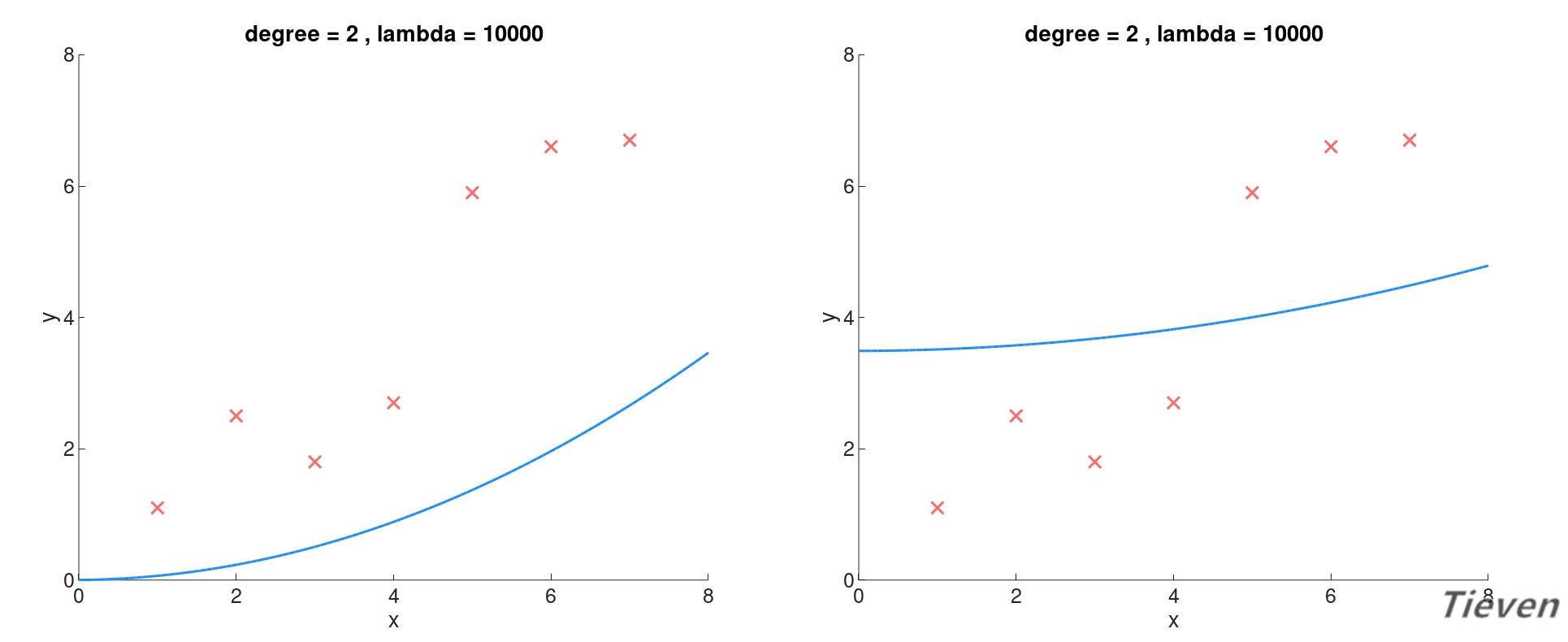
  左图为所有参数都参与正则化的结果，因为正则化参数非常大，为了最小化代价函数，所有的参数都趋向于0。模型是经过原点的曲线，无法体现出样本的平均水平。

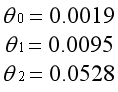
  右图为θ0不参与正则化的结果，因为正则化参数非常大，为了最小化代价函数，除了θ0外的参数都趋向于0。虽然模型的表现也很差，至少体现出样本的平均水平。

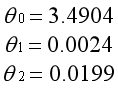
  注意在理论说明时向量的下标是从0开始计数，在代码编写时向量的下标是从1开始计数。向量θ中的第一个元素即常数项对应的参数，这个元素不参与正则化。

  将线性回归的函数更新如下：

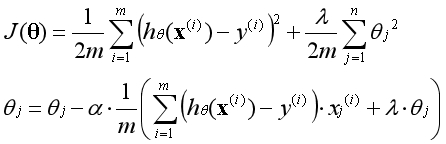
  将逻辑回归的函数更新如下：

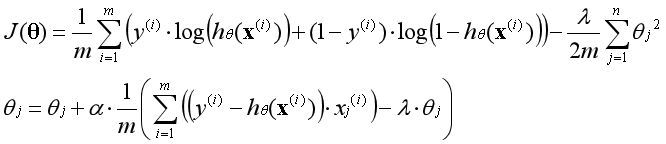
函数与导数

  当函数只有一个变量时，在二维空间中可以表现为一条曲线。假设函数在f(θ)=0处有解，已知导数是切线的斜率，根据这一点可以寻找到函数在该点的解。

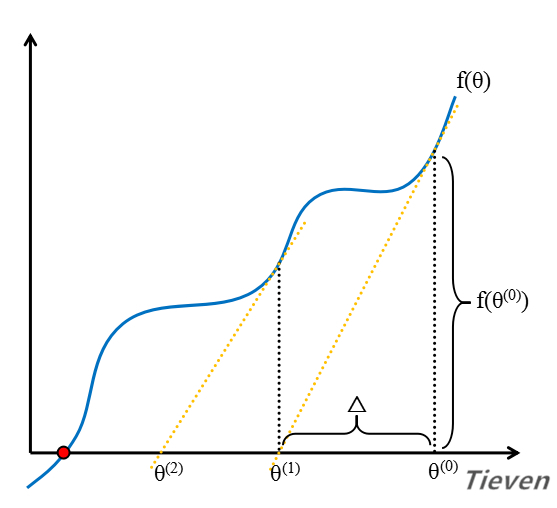
  首先随机选择一个初始值作为第一个交点。

  求出函数在第一个交点的导数，将切线延长到x轴上，可以得到第二个交点。

  求出函数在第二个交点的导数，将切线延长到x轴上，可以得到第三个交点。

  在这个过程中，交点在不断地向目标靠近。如此反复，最终得到函数在f(θ)=0处的解。单变量的牛顿法迭代形式如下：

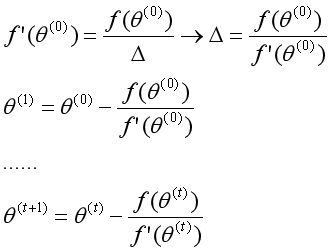
牛顿方法

  这个方法如何应用到逻辑回归算法中？当一阶导数为0时，函数处于极值点。要求代价函数的最优解，可转化为求一阶导数为0，这又可通过牛顿方法用二阶导数进行迭代。

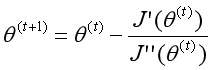
  所以问题的关键在于如何求代价函数的二阶导数。因为代价函数中有多个变量，每个变量都有相对于其他变量的二阶偏导数。这些二阶偏导数表现为矩阵的形式，以两个变量为例。

  右边的符号表示第j个变量相对于第i个变量的二阶偏导数。虽然形式复杂，但本质上在求一个变量的偏导数时，是直接将其他变量视为常数，这就极大地简化了问题。

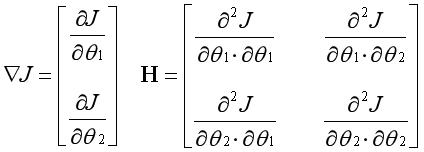
  左边是一阶导数向量，右边是二阶导数矩阵（Hessian Matrix），多维下的牛顿方法可表示为以下形式：

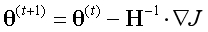
  逻辑回归一阶导数：

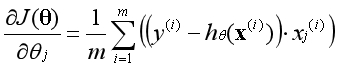
  逻辑回归二阶导数：

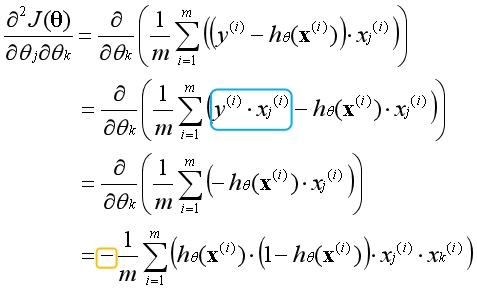
  蓝色部分相对于变量是常数项可以直接消去，等式最外面有一个负号不要遗漏了。现在的问题是该如何得到整个二阶导数矩阵呢？构造一个小规模的样本观察一下规律。

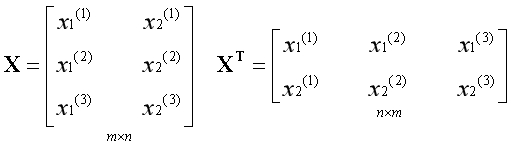
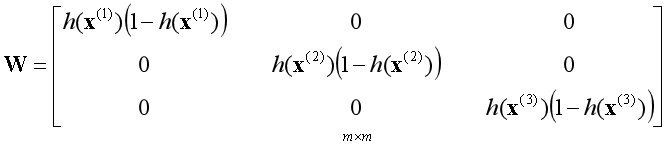
  假设j=1，k=2，将对应的二阶偏导数函数展开：

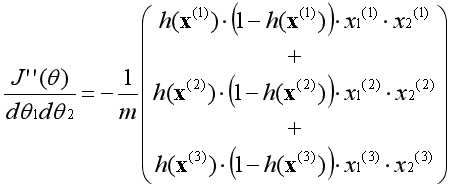
  观察上式，发现只有一种矩阵的组合方法满足要求，即：

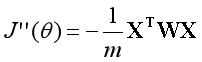
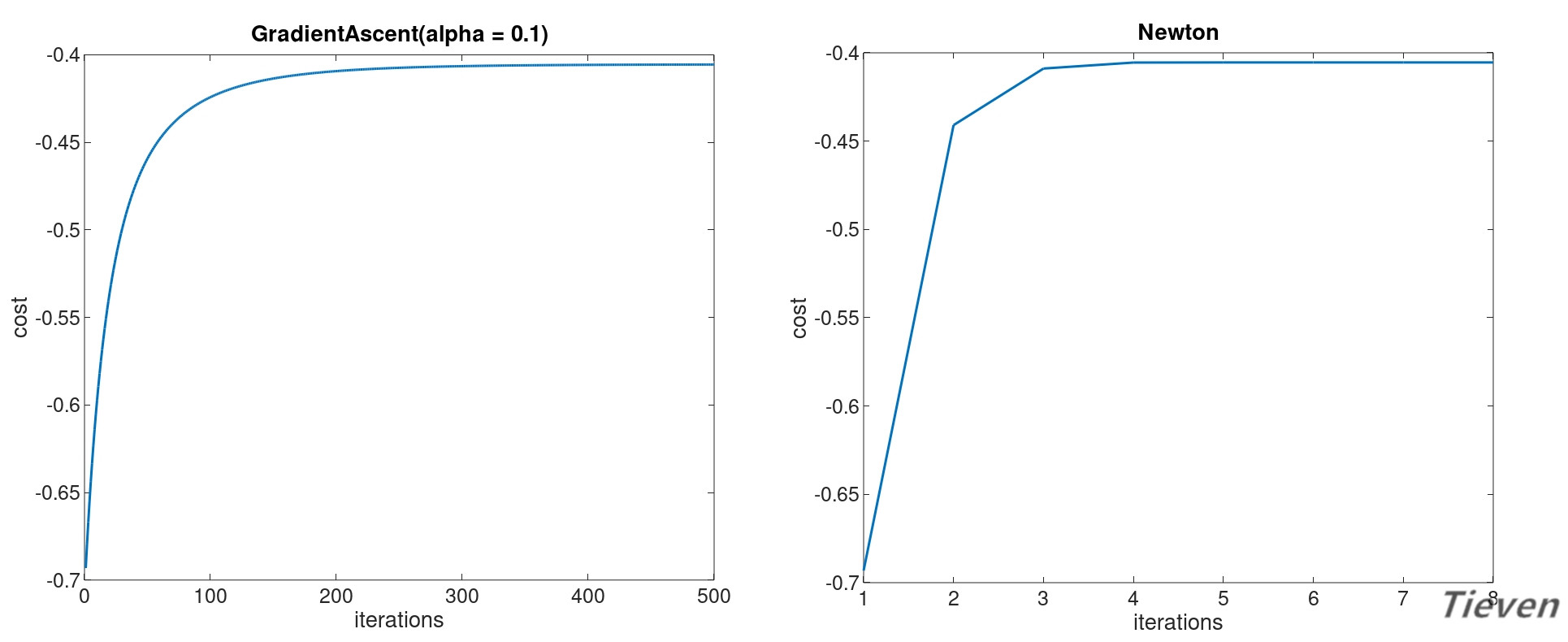
  相比梯度上升法，牛顿方法的优点是不需要设置学习率，且所需迭代次数远远少于前者。缺点是需要计算二阶导数的逆矩阵，为避免求逆又衍生出了许多的改良版本。

总结

  正则化通过为参数支付一个代价，使得参数尽量最小化。参数是特征的权重，当权重降低的时候，特征对于模型的影响也随之降低。当模型复杂度降低时，往往能获得更好的表现。

  牛顿方法是通过二阶导数来更新参数的方法，在大规模机器学习问题中，求解二阶导数的逆矩阵难以实现，实际中常用的是伪牛顿法，如BFGS，L-BFGS等等。

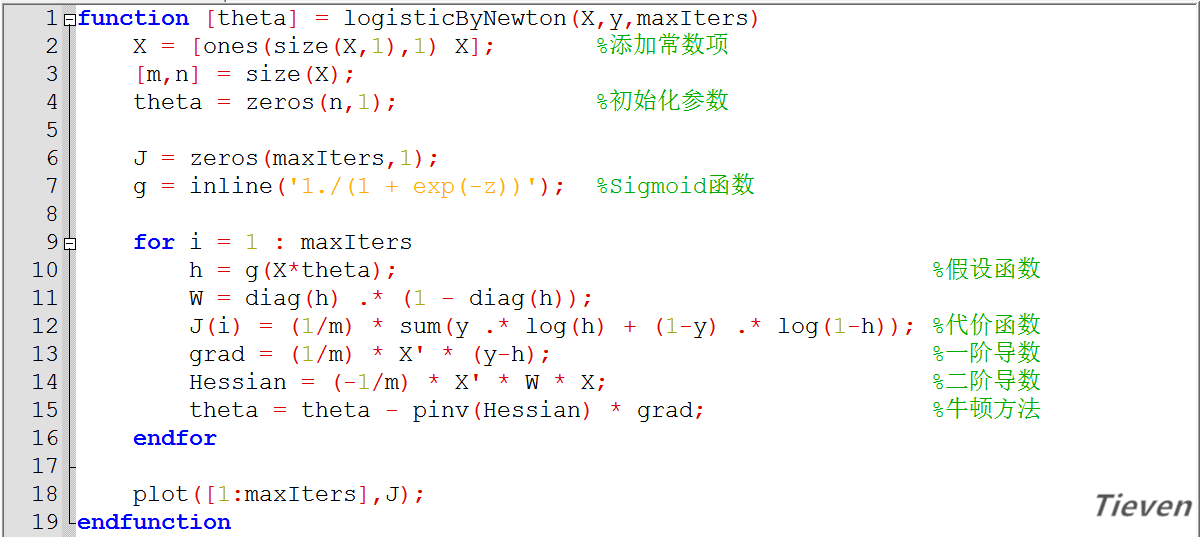
非正规代码

版权声明

  1，本文为原创文章，未经作者授权禁止引用、复制、转载、摘编。

  2，对于有上述行为者，作者将保留追究其法律责任的权利。

Tieven

2019.1.9

tieven.it@gmail.com