Tree Traversals Again

An inorder binary tree traversal can be implemented in a non-recursive way with a stack. For example, suppose that when a 6-node binary tree (with the keys numbered from 1 to 6) is traversed, the stack operations are: push(1); push(2); push(3); pop(); pop(); push(4); pop(); pop(); push(5); push(6); pop(); pop(). Then a unique binary tree (shown in Figure 1) can be generated from this sequence of operations. Your task is to give the postorder traversal sequence of this tree.

Figure 1

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (≤) which is the total number of nodes in a tree (and hence the nodes are numbered from 1 to N). Then 2 lines follow, each describes a stack operation in the format: "Push X" where X is the index of the node being pushed onto the stack; or "Pop" meaning to pop one node from the stack.

Output Specification:

For each test case, print the postorder traversal sequence of the corresponding tree in one line. A solution is guaranteed to exist. All the numbers must be separated by exactly one space, and there must be no extra space at the end of the line.

Sample Input:

Push
Push
Push
Pop
Pop
Push
Pop
Pop
Push
Push
Pop
Pop

Sample Output:

可以使用堆栈以非递归方式实现顺序二进制树遍历。你的任务是给出这棵树的后序遍历序列。

每个输入文件包含一个测试用例。对于每种情况，第一行包含正整数N（≤ 3 0），它是节点的总数量在树（并且因此节点编号从1到N）。然后接下来是N行，每行描述一种堆栈操作，格式为：“Push X”，其中X是被推入堆栈的节点的索引; 或“Pop”表示从堆栈中弹出一个节点。

对于每个测试用例，在一行中打印相应树的后序遍历序列。保证存在解决方案。所有数字必须用一个空格分隔，并且在行的末尾不能有额外的空格。

先给出大神的思路

对二叉树的中序遍历可以通过使用栈来避免迭代的方法，对于figure1中的6节点树而言，它的栈操作为push(1); push(2); push(3); pop(); pop(); push(4); pop(); pop(); push(5); push(6); pop(); pop()。依据这个输入可以生成这个二叉树，要求打印出该树的后序遍历。

解法：

该题要求我们通过中序遍历的栈实现的栈操作来生成二叉树。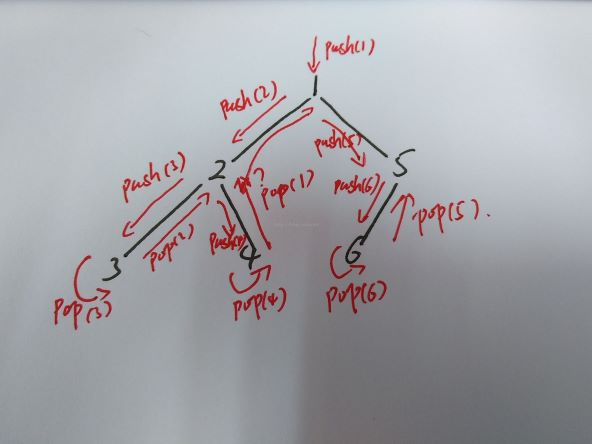

如上图，中序遍历的操作流程（其中箭头代表遍历流），我们可以看出：

1.每次push都指向一个新的节点。

2.每次pop都指向一个被抛出的节点。

3.连续的pop-pop或push-push流的方向都相同。

4.连续的push-pop指向同一个叶节点，同时执行方向转弯。（节点3）

5.连续的pop-push经过一个父节点，同时执行方向转弯。（节点2）

6.每个节点只能pop指向一次，push指向一次。（节点4到2直接跳到1）

于是我们就可以通过这些特性来构建二叉树：

1.读入第一次push构建根节点，根节点入栈。

2.读入下一个操作,有两种情况:

（1）push

说明有一个新节点出现，构建一个节点。如果上次操作为push,把该节点设为栈顶的左儿子，节点入栈。如果上次是pop，经过一个父节点，说明应该是生成了父节点的一个儿子，所以将该节点设为上次pop出来的节点的右儿子。

（2）pop

说明正在pop一个节点，不论上次操作是，该次都抛出一个节点。

这是我写的，有点菜

 #include <iostream>
 #include <stack>
 #include <string>
 #include <algorithm>
 #define MaxTree 31
 #define Null -1
 using namespace std;
 
 int P[MaxTree];
 int num=;
 int NUM=;
 stack<int> st;
 
 struct TreeNode
 {
     int date;
     int Left;
     int Right;
 }T[MaxTree];
 
 int BuildTree(struct TreeNode T[])
 {
     int N,m,p,i;
     string str,pre;
     int Root;
     cin>>N;
     for(i=;i<*N;i++)
     {
         cin>>str;
         if(str=="Push")
         {
             cin>>m;
             if(i==)
             {
                 Root=;
                 T[num].date=m;
                 T[num].Left=Null;
                 T[num].Right=Null;
                 st.push(num);
                 pre=str;
             }
             else if(pre=="Push")
             {
                 T[num].Left=num+;
                 num++;
                 T[num].date=m;
                 T[num].Left=Null;
                 T[num].Right=Null;
                 st.push(num);
                 pre=str;
             }
             else if(pre=="Pop")
             {
                 T[p].Right=num+;
                 num++;
                 T[num].date=m;
                 T[num].Left=Null;
                 T[num].Right=Null;
                 st.push(num);
                 pre=str;
             }
         }
         else if(str=="Pop")
         {
             p=st.top();
             st.pop();
             pre=str;
         }
     }
     if(N==)
     {
         Root=Null;
     }
     return Root;
 }
 
 void search(int Tree)
 {
     if(Tree==Null)
         return;
     search(T[Tree].Left);
     search(T[Tree].Right);
     P[NUM++]=T[Tree].date;
 }
 
 int main()
 {
     int Tree;
     Tree=BuildTree(T);
     search(Tree);
     int i;
     for(i=;i<NUM;i++)
     {
         if(i==)
             cout<<P[i];
         else
             cout<<' '<<P[i];
     }
     return ;
 }

下面是别人用动态链表实现的，值得一看

 #include <cstdio>
 #include <stack>
 using namespace std;
 
 int preorder[], inorder[];
 int n, preid = , inid = , cnt = ;
 int get(){
     char s[];
     scanf("%s", s);
     if (s[] == 'o') return -;
     int a;
     scanf("%d", &a);
     return a;
 }
 void build(int preb, int pree, int inb, int ine){
     if (preb > pree) return;
     int root = preorder[preb];
     int inroot = inb;
     while (inorder[inroot] != root) ++inroot;
     build(preb+, preb+inroot-inb, inb, inroot-);
     build(preb+inroot-inb+, pree, inroot+, ine);
     if (cnt++ != ) putchar(' ');
     printf("%d", root);
 }
 int main(){
     scanf("%d", &n);
     stack<int> st;
     for (int i = ; i < n*; ++i){
         int a = get();
         if (a != -){
             st.push(a);
             preorder[preid++] = a;
         }else{
             inorder[inid++] = st.top();
             st.pop();
         }
     }
     build(, n-, , n-);
     return ;
 }

 #include <string>
 #include <iostream>
 #include <stack>
 using namespace std;
 
 const string PUSH("Push");
 const string POP("Pop");
 
 typedef struct Node
 {
     int data;
     Node* left;
     Node* right;
     Node(int d):data(d), left(NULL), right(NULL){}
 }Node;
 
 void PostOrderTraverse(Node *root)
 {
     Node* temp = root;
     Node* pre = NULL;
     stack<Node*> S;
     int flag = ;
 
     while(temp || !S.empty())
     {
         if(temp)
         {
             S.push(temp);
             temp = temp->left;
         }
         else
         {
             temp = S.top();
             if(temp->right && temp->right != pre)
                 temp = temp->right;
             else
             {
                 if(!flag)
                 {
                     flag = ;
                     cout<< temp->data;
                 }
                 else
                     cout<<" "<<temp->data;
                 S.pop();
                 pre = temp;
                 temp = NULL;
             }
         }
     }
     cout<<endl;
 }
 
 int main()
 {
     int n, data;
     string act;
     stack<Node*> S;
     Node* root = NULL, *pre = NULL;
     int l = , r = ;
     cin >> n;
 
     //First, build the tree , root of tree is *root.
     for(int i=; i <= *n; i++)
     {
         Node* temp;
         cin >> act;
         if(act == PUSH)
         {
             cin >> data;
             temp = new Node(data);
             if(i == )
             {
                 root = temp;
             }
 
             S.push(temp);
             if(pre)
             {
                 if(l == )
                     pre->left = temp;
                 else
                     pre->right = temp;
             }
             l = ;
             pre = temp;
         }
         else if(act == POP)
         {
             pre = S.top();
             S.pop();
             l = ;
         }
     }
 
     PostOrderTraverse(root);
 
     system("pause");
     return ;
 }