[LeetCode] Binary Tree Pruning 二叉树修剪

We are given the head node root of a binary tree, where additionally every node's value is either a 0 or a 1.

Return the same tree where every subtree (of the given tree) not containing a 1 has been removed.

(Recall that the subtree of a node X is X, plus every node that is a descendant of X.)

Example 1:
Input: [1,null,0,0,1]
Output: [1,null,0,null,1]

Explanation:
Only the red nodes satisfy the property "every subtree not containing a 1".
The diagram on the right represents the answer.

Example 2:
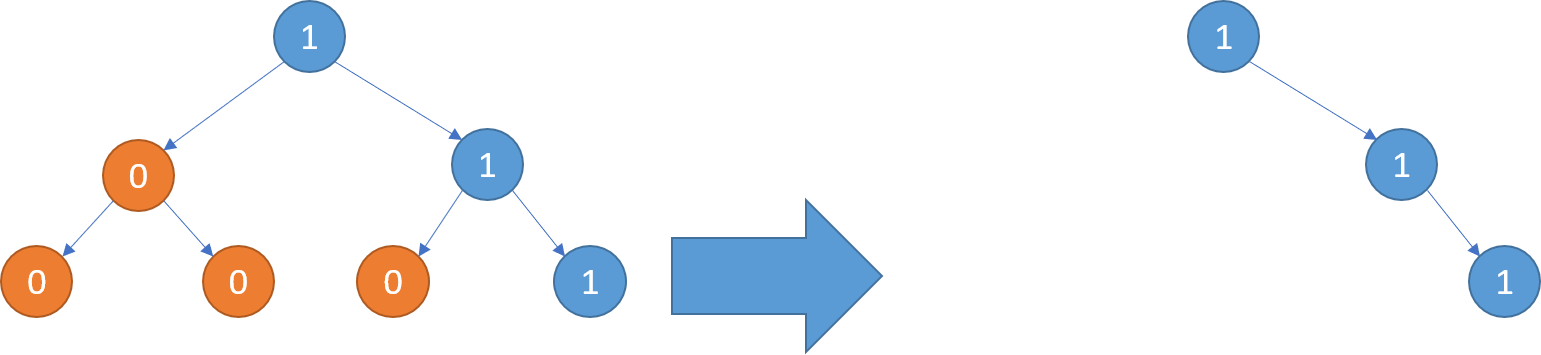
Input: [1,0,1,0,0,0,1]
Output: [1,null,1,null,1]

Example 3:
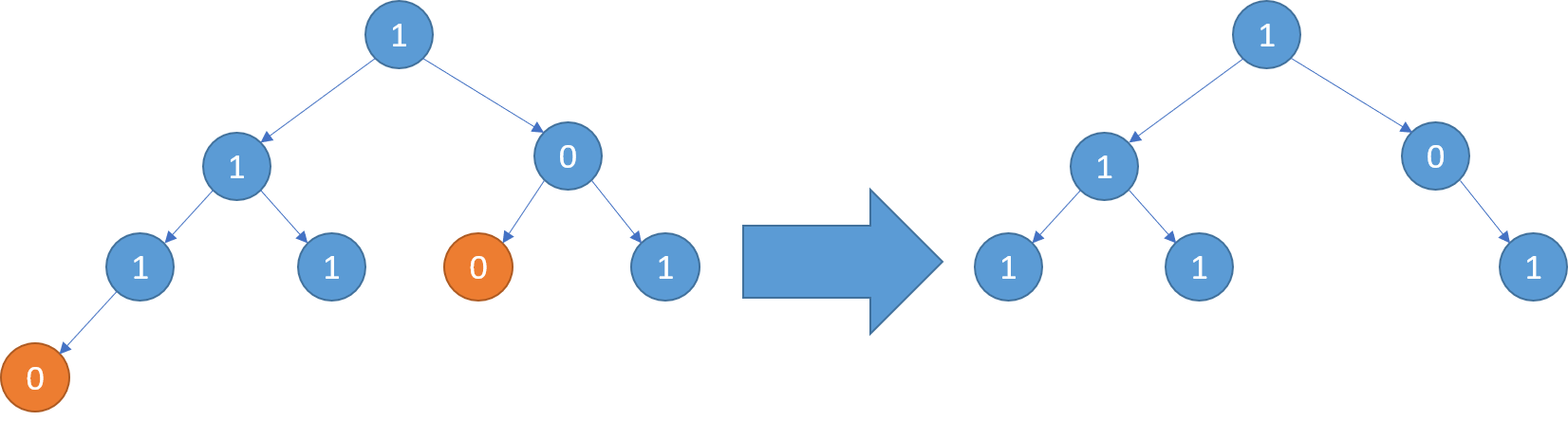
Input: [1,1,0,1,1,0,1,0]
Output: [1,1,0,1,1,null,1]

Note:

• The binary tree will have at most 100 nodes.
• The value of each node will only be 0 or 1.

这道题给了我们一棵二叉树，说是结点只有0或者1，让我们移除所有没有含有结点1的子树。题目中也给了一些图例，不难理解。这道题的难点就在于怎么看待没有结点1的子树，我们知道子树也是由一个个结点组成的，需要明确的是一个单独的叶结点也可算作是子树，所以值为0的叶结点一定要移除，就像上面的例子1和3中的几个叶结点要被移除一样。对于例子2来说，如果移除了第三行的3个叶结点后，那么第二行的那个值为0的结点也变成了叶结点，继续移除即可，所以与其找值全为0的子树，我们可以不断的移除值为0的叶结点，全都移除后那么值全为0的子树也就都被移除了。

好，想通了这一点后，我们看如何来实现。对于玩二叉树的题，十有八九都是用递归，所以我们应该首先就考虑递归的解法，然后再想按什么顺序来遍历二叉树呢？层序，先序，中序，还是后序？根据这道题的特点，我们要从末尾来一层一层的移除值为0的叶结点，所以天然时候用后序遍历。那么想到这里，解题思路跃然纸上了吧，我们首先对结点判空，如果不存在，直接返回空。然后分别对左右子结点调用递归函数，此时判断，如果当前结点是值为1的叶结点，那么移除该结点，即返回空，否则返回原结点即可，参见代码如下：

class Solution {
public:
    TreeNode* pruneTree(TreeNode* root) {
        if (!root) return NULL;
        root->left = pruneTree(root->left);
        root->right = pruneTree(root->right);
        return (!root->left && !root->right && root->val == ) ? NULL : root;
    }
};

参考资料：

https://leetcode.com/problems/binary-tree-pruning/

https://leetcode.com/problems/binary-tree-pruning/discuss/122730/C++JavaPython-Self-Explaining-Solution-and-2-lines

LeetCode All in One 题目讲解汇总(持续更新中...)