Luogu 1494 - 小Z的袜子 - [莫队算法模板题][分块]

题目链接：https://www.luogu.org/problemnew/show/P1494

题目描述

作为一个生活散漫的人，小Z每天早上都要耗费很久从一堆五颜六色的袜子中找出一双来穿。终于有一天，小Z再也无法忍受这恼人的找袜子过程，于是他决定听天由命……

具体来说，小Z把这N只袜子从1到N编号，然后从编号L到R(L 尽管小Z并不在意两只袜子是不是完整的一双，甚至不在意两只袜子是否一左一右，他却很在意袜子的颜色，毕竟穿两只不同色的袜子会很尴尬。

你的任务便是告诉小Z，他有多大的概率抽到两只颜色相同的袜子。当然，小Z希望这个概率尽量高，所以他可能会询问多个(L,R)以方便自己选择。

然而数据中有L=R的情况，请特判这种情况，输出0/1。

输入输出格式

输入格式：

输入文件第一行包含两个正整数N和M。N为袜子的数量，M为小Z所提的询问的数量。接下来一行包含N个正整数Ci，其中Ci表示第i只袜子的颜色，相同的颜色用相同的数字表示。再接下来M行，每行两个正整数L，R表示一个询问。

输出格式：

包含M行，对于每个询问在一行中输出分数A/B表示从该询问的区间[L,R]中随机抽出两只袜子颜色相同的概率。若该概率为0则输出0/1，否则输出的A/B必须为最简分数。（详见样例）

输入输出样例

输入样例#1：

6 4
1 2 3 3 3 2
2 6
1 3
3 5
1 6

输出样例#1：

2/5
0/1
1/1
4/15

说明

30%的数据中 N,M ≤ 5000；

60%的数据中 N,M ≤ 25000；

100%的数据中 N,M ≤ 50000，1 ≤ L < R ≤ N，Ci ≤ N。

题解：

直接上线段树的话，由于不满足区间可加性：

假设现在要计算区间 $[L,R]$ 里每一种颜色的袜子的数量，此时我们已经分别维护好了左右两边区间 $[L,mid]$ 和 $[mid+1,R]$ 中每一种颜色的袜子的数量，然后开始向上维护：

就会发现，依然要把每种颜色的袜子在左右区间的数量加起来才能完成对一个父节点的维护，我们并不能在 $O(1)$ 的时间内完成对线段树单一节点的维护。

但此时，若已知一个区间 $[ L , R ]$ 的情况，我们可以在 $O(1)$ 的时间内确定的有 $[ L , R+1 ]$ 和 $[ L , R-1 ]$ 和 $[ L-1 , R ]$ 和 $[ L+1 , R ]$ 的情况，

假设我们现在已知 $[ L , R ]$ 的情况，需要计算的是 $[ L' , R' ]$ 的情况，易知所需时间复杂度为 $O( | L - L' | + | R - R' | )$，

那么怎么样能够较快地回答 $M$ 次询问呢？

考虑将整个长度为 $N$ 的分成 $\frac{N}{S}$ 块，每一块长度为 $S$，所有的询问先按左端点所属分块的编号进行升序排序，对于分块编号相同的，则按右端点的大小升序排序，

那么，经过排序之后按照新的顺序遍历所有询问，每次回答当前的询问，都要以上一次询问为基础，分别考虑从上一次询问到当前询问的转移中左右两个端点的变动：

对于左端点：

　　上一次询问和当前询问同属一个分块时，注意左端点不是有序的，那么最多从块的一端移到另一端 $O(S)$；

　　即使跨块，考虑询问的左端点是随机生成的，当 $M$ 和 $N$ 同数量级时，一般来说每个分块下面都应当存在大约 $\frac{MS}{N}$ 个询问，那么前后两次询问的转移基本就是两个相邻块间的转移，因此移动距离也是 $O(S)$；

　　总共有 $M$ 个询问，总的时间复杂度是 $O(MS)$。

对于右端点：

　　上一次询问和当前询问同属一个分块时，同个分块内的右端点是有序的，那么易知遍历一个分块中所有询问，右端点最多就是从 $1$ 一直移动到 $N$，一整个分块内右端点移动 $O(N)$ 次；

　　而遇到上一次询问和当前询问是跨块的情形，最差的情况不过就是右端点从 $N$ 回到 $1$，也是 $O(N)$ 次；

　　共 $O(\frac{N}{S})$ 个分块，所有前后两次询问的变动属于分块内变动的，合起来使得右端点共移动 $O(\frac{N^2}{S})$ 次；

　　最多 $O(\frac{N}{S})$ 次跨块变动，所有前后两次询问的变动为跨快变动的，合起来使得右端点共移动 $O(\frac{N^2}{S})$ 次；

　　两者加起来，时间复杂度依然 $O(\frac{N^2}{S})$。

综上，莫队的时间复杂度是 $O(MS + \frac{N^2}{S})$，取 $S = \frac{N}{\sqrt M}$，可使得时间复杂度最小为 $O(N \sqrt M)$。

那么假设某个区间 $[L,R]$ 有 $X(X \ge 2)$ 只不同袜子，那么任取两只袜子的情况数是 $C_X^2$，

假设区间内的袜子有 $1 \sim K$ 共 $K$ 种颜色，假设第 $k$ 个颜色的袜子数为 $num[k]$，那么取到同种颜色的两只袜子的可能数是 $C_{num\left[ 1 \right]}^2 + C_{num\left[ 2 \right]}^2 + \cdots + C_{num\left[ K \right]}^2$ ，

根据组合数公式可知 $C_n^2 = \frac{{n\left( {n - 1} \right)}}{2}$ ，

所以取到两只同色袜子的概率为

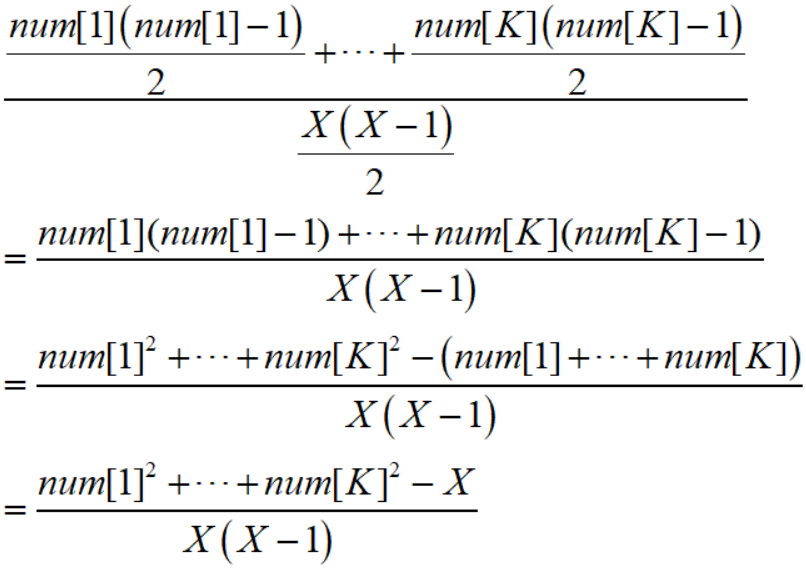
由于 $X = R - L + 1$ ，我们实际要查询的就是 $Q\left( {L,R} \right) = \sum\limits_{k = 1}^K {num\left[ k \right]^2 }$ ，

那么，

若区间转移时增加一只颜色为 $c$ 的袜子：

$Q\left( {L,R + 1} \right) = Q\left( {L - 1,R} \right) = Q\left( {L,R} \right) - num\left[ c \right]^2 + \left( {num\left[ c \right] + 1} \right)^2 = Q\left( {L,R} \right) + 2 \times num\left[ c \right] + 1$

若区间转移时减少一只颜色为 $c$ 的袜子：

$Q\left( {L,R - 1} \right) = Q\left( {L{\rm{ + }}1,R} \right) = Q\left( {L,R} \right) - num\left[ c \right]^2 + \left( {num\left[ c \right] - 1} \right)^2 = Q\left( {L,R} \right) - 2 \times num\left[ c \right] + 1$

AC代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
 
const int maxn=+;
const int maxm=+;
 
struct Query
{
    int block; //表示左端点所在块
    int id; //表示询问的原始顺序
    int l,r;
    Query(){}
    Query(int _blk,int _id,int _l,int _r){block=_blk,id=_id,l=_l,r=_r;}
    bool operator <(const Query &oth)const
    {
        return (block==oth.block)?(r<oth.r):(block<oth.block);
    }
};
vector<Query> Q;
 
int n,m;
int c[maxn],num[maxn];
ll up[maxn],down[maxn];
 
inline ll gcd(ll a,ll b){return b==?a:gcd(b,a%b);}
 
int main()
{
    while(cin>>n>>m)
    {
        int len=n/sqrt(m);
        for(int i=;i<=n;i++) scanf("%d",&c[i]);
        Q.clear();
        for(int i=,l,r;i<=m;i++)
        {
            scanf("%d%d",&l,&r);
            Q.push_back(Query(l/len,i,l,r));
        }
        sort(Q.begin(),Q.end());
 
        memset(num,,sizeof(num));
        int pl=,pr=;
        ll ans=;
        for(int i=;i<Q.size();i++)
        {
            const Query& q=Q[i];
            if(q.l==q.r)
            {
                up[q.id]=;
                down[q.id]=;
                continue;
            }
            down[q.id]=(ll)(q.r-q.l+)*(q.r-q.l);
            if(pr<q.r)
            {
                for(int j=pr+;j<=q.r;j++)
                {
                    ans=ans+*num[c[j]]+;
                    num[c[j]]++;
                }
            }
            if(pr>q.r)
            {
                for(int j=pr;j>q.r;j--)
                {
                    ans=ans-*num[c[j]]+;
                    num[c[j]]--;
                }
            }
            if(pl>q.l)
            {
                for(int j=pl-;j>=q.l;j--)
                {
                    ans=ans+*num[c[j]]+;
                    num[c[j]]++;
                }
            }
            if(pl<q.l)
            {
                for(int j=pl;j<q.l;j++)
                {
                    ans=ans-*num[c[j]]+;
                    num[c[j]]--;
                }
            }
            up[q.id]=ans-(q.r-q.l+);
 
            pl=q.l;
            pr=q.r;
        }
 
        for(int i=;i<=m;i++)
        {
            ll g=gcd(up[i],down[i]);
            printf("%lld/%lld\n",up[i]/g,down[i]/g);
        }
    }
}