js计算斐波拉切

		function feibo(a){

			if(!a || a <= 0){
				 throw new Error("参数错误，必须大于0");
			}else if(a == 1){
				return 1;
			}else if(a == 2){
				return 2;
			}else{
				return feibo(a-1) + feibo(a-2);
			}
		}
		console.log(feibo(7));

　　

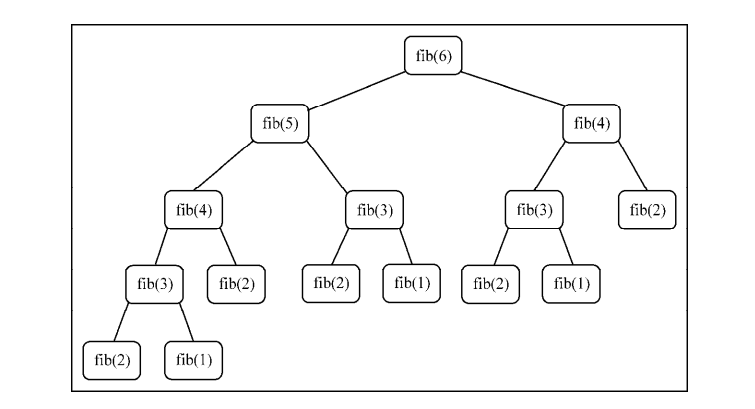
方法二：迭代法

	function feibo(n){
			if(n <= 2){
				return 1;
			}
			var s1 = 1;
			var s2 = 1;
			for(var i = 3; i <= n; i++){
				s2 = s2  + s1;
				s1 = s2 - s1;
			}
			return s2;
		}

		console.log(feibo(6));