（原）Show, Attend and Translate: Unsupervised Image Translation with Self-Regularization and Attention

转载请注明出处：

https://www.cnblogs.com/darkknightzh/p/9333844.html

论文网址：https://arxiv.org/abs/1806.06195

在gan中，对图像进行风格变换时，一般都是将整个图像进行变换。由于图像包含前景和背景，因而该论文在保持背景区域不变的前提下，对前景区域进行风格变换。同时，使用self-regularization项来约束变换前后背景区域的差异。

网络结构如下图所示。输入图像通过2层的下采样，而后通过9层的残差网络，在通过2层的上采样，得到。另一方面，通过预训练的vgg-19网络的前几层，并通过2层的上采样，在通过conv+sigmoid，得到Gattn，即前景区域的概率图。网络基本结构均为conv+bn+relu。残差部分使用空洞卷积，因为空洞卷积可以增加感受野的大小。损失函数包含两部分，传统的判别器的损失及感知损失。文中指出，感知损失比传统的距离更接近人类对相似性的认知。传统的判别网络为5层的CNN网络。

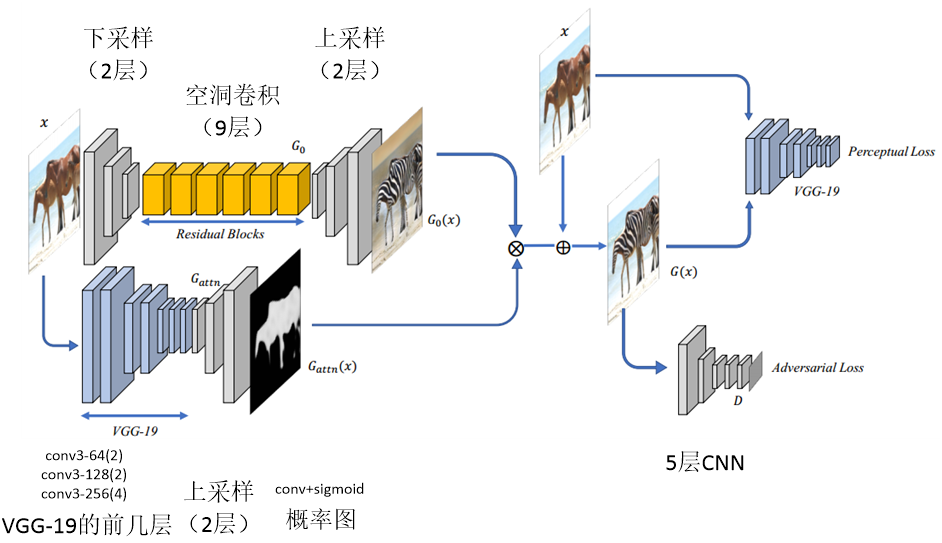
其中，

$G(x)={{G}_{attn}}(x)\otimes {{G}_{0}}(x)+(1-{{G}_{attn}}(x))\otimes x$

${{G}_{attn}}(x)\otimes {{G}_{0}}(x)$代表前景区域，$(1-{{G}_{attn}}(x))\otimes x$代表背景区域。${{G}_{attn}}(x)$为前景区域的概率图，像素范围为[0, 1]。

文中判别器：

${{L}_{D}}=\log (D(y))-\log (1-D(G(x)))$

生成器：

${{L}_{G}}={{l}_{adv}}(G(x),y)+\lambda {{l}_{reg}}(x,G(x))$

生成器包含两部分，传统gan的损失：

${{l}_{adv}}(G(x),y)=-\log (-D(G(x)))$

及self-regularization项损失：

${{l}_{reg}}(G(x),x)=\sum\limits_{l=1,2,3}{\frac{1}{{{H}_{l}}{{W}_{l}}}\sum\limits_{h,w}{(\left\| {{w}_{l}}\circ (\hat{F}(x)_{hw}^{l}-\hat{F}(G(x))_{hw}^{l}) \right\|_{2}^{2})}}$

${{l}_{reg}}$使用预训练的vgg-19网络的前三层加权得到。分别将输入图像x及生成的图像$G(x)$通过vgg-19网络前3层，得到对应的特征图，并计算特征图的l2 norm的平方，之后进行加权。各层权重经过大量实验得到为：

$({{w}_{1}},{{w}_{2}},{{w}_{3}})=(1/32,1/16,1/8)$

训练过程：先训练${{G}_{0}}$，再训练${{G}_{attn}}$，最后finetune整个网络。对于$\lambda $，从0增加，直至对抗损失降低到阈值$l_{adv}^{t}$之下，而后固定$\lambda $。