浅谈k短路算法

An Old but Classic Problem

　　给定一个$n$个点，$m$条边的带正权有向图。给定$s$和$t$，询问$s$到$t$的所有权和为正路径中，第$k$短的长度。

Notice

　　定义两条路径不同，当且仅当它们的边集中存在一条边，使得它只在其中的一条路径上。

Solution#1 Shortest Path & A*

　　对于Dijstra算法，有一个结论就是，当一个点第$k$次出队的时候，此时路径长度就是$s$到它的第$k$短路。

　　那为什么还要A*呢？我试了试，写了个Dijstra，然后交了一发poj 2449，于是MLE了。。。如果您觉得我的Dijstra太丑了，您可以手写一个交一发。

　　所以用A*来优化优化状态数（其实就是玄学优化，需要你的人品还有出题人的素质）。

　　首先建反图，跑一次最短路算法，得到每个点到$t$的最短路的距离。

　　然后用当前走的距离加上到终点的最短路的长度作为优先级进行A*。

　　那如何得到答案？

当一个点第k次出队时，答案是它的优先级
当终点第k次出队时，答案是它已经走的路程

　　据说A*可以被卡成$O\left(nk\log n \right )$，只是我不会QAQ。

Code

 /**

  * poj

  * Problem#2449

  * Accepted

  * Time: 250ms

  * Memory: 9252k

  */

 #include <iostream>

 #include <fstream>

 #include <sstream>

 #include <algorithm>

 #include <cstdio>

 #include <cstdlib>

 #include <cstring>

 #include <ctime>

 #include <cctype>

 #include <cmath>

 #include <vector>

 #include <queue>

 #include <stack>

 #include <map>

 #include <set>

 #include <bitset>

 using namespace std;

 typedef bool boolean;

 typedef class Edge {

     public:

         int end;

         int next;

         int w;

         Edge(int end = , int next = -, int w = ):end(end), next(next), w(w) {        }

 }Edge;

 const int N = 1e3, M = 1e5;

 typedef class MapManager {

     public:

         int cnt;

         int h[N + ];

         Edge edge[M + ];

         MapManager() {        }

         MapManager(int n):cnt(-) {

 //            h = new int[(n + 1)];

 //            edge = new Edge[(m + 1)];

             memset(h, -, sizeof(int) * (n + ));

         }

         inline void addEdge(int u, int v, int w) {

             edge[++cnt] = (Edge(v, h[u], w));

 //            h[u] = (signed)edge.size() - 1;

             h[u] = cnt;

         }

         inline int start(int node) {    return h[node];        }

         Edge& operator [] (int pos) {

             return edge[pos];

         }

 }MapManager;

 #define m_endpos -1

 int n, m;

 MapManager g;

 MapManager rg;

 int s, t, k;

 int ds[N + ];

 inline void init() {

     scanf("%d%d", &n, &m);

     memset(g.h, -, sizeof(int) * (n + ));

     memset(rg.h, -, sizeof(int) * (n + ));

     for(int i = , u, v, w; i <= m; i++) {

         scanf("%d%d%d", &u, &v, &w);

         g.addEdge(u, v, w);

         rg.addEdge(v, u, w);

     }

     scanf("%d%d%d", &s, &t, &k);

 //    ds = new int[(n + 1)];

 }

 #define g rg

 #define f ds

 #define que que1

 boolean vis[N + ];

 queue<int> que;

 boolean spfa(int s, int t) {

     memset(f, 0x7f, sizeof(int) * (n + ));

     memset(vis, false, sizeof(boolean) * (n + ));

     que.push(s);

     f[s] = ;

     while(!que.empty()) {

         int e = que.front();

         que.pop();

         vis[e] = false;

         for(int i = g.start(e); i != m_endpos; i = g[i].next) {

             int& eu = g[i].end;

 //            cout << e << " " << eu << " " << i <<endl;

             if(f[e] + g[i].w < f[eu]) {

                 f[eu] = f[e] + g[i].w;

                 if(!vis[eu]) {

                     que.push(eu);

                     vis[eu] = true;

                 }

             }

         }

     }

     return (f[t] != 0x7f7f7f7f);

 }

 #undef g

 #undef f

 #undef que

 typedef class Status {

     public:

         int node;

         int dis;

         int priority;

         Status(int node = , int dis = ):node(node), dis(dis), priority(h()) {        }

         int h() {

             return dis + ds[node];

         }

         boolean operator < (Status b) const {

             return priority > b.priority;

         }

 }Status;

 int label[N + ];

 priority_queue<Status> que;

 int bfs(int s, int t) {

     if(s == t)    k++;

 //    label = new int[(n + 1)];

     memset(label, , sizeof(int) * (n + ));

     que.push(Status(s, ));

     while(!que.empty()) {

         Status e = que.top();

         que.pop();

         label[e.node]++;

         if(e.node == t && label[e.node] == k)

             return e.dis;

         for(int i = g.start(e.node); i != m_endpos; i = g[i].next) {

             if(label[g[i].end] < k)

                 que.push(Status(g[i].end, e.dis + g[i].w));

         }

     }

     return -;

 }

 inline void solve() {

     if(!spfa(t, s)) {

         puts("-1");

         return;

     }

     printf("%d", bfs(s, t));

 }

 int main() {

     init();

     solve();

     return ;

 }

最短路算法 + A*

Solution#2 Shortest Path & Protractable Heap

　　考虑建立反图，然后跑最短路算法得到以$t$为根的最短路径生成树。

　　当走了一条非树边$(u, v, w)$意味着什么？

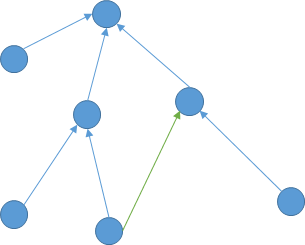
　　最终的路径长度就会因此增加$f[v] - f[u] + w$。

　　对于一条路径，我们依次将它经过的非树边记下来，约定得到的序列是这条路径的非树边序列。

　　考虑对于一个合法的非树边序列，我们可以找到唯一的一条$s$到$t$的路径与之对应。

　　因此，$k$短路的长度就等于第$k$小的代价和加上$s$到$t$的最短路的长度。

　　考虑如何来得到一个合法的非树边序列。

找到一条起点在当前点$p$到根$t$的路径上的非树边
令p等于这条边的终点。

　　我们可以通过这样的方法来得到所有的非树边序列。但是我们并不需要所有的非树边序列，因此当找到第$x$短路后再进行拓展状态，然后用优先队列来维护。

　　但是这样每次拓展时间复杂度可达$O(m)$，总时间复杂度可以达到$O\left(mk\log \left (mk \right ) \right )$。

　　令人无法接受。但是其中真正会被用到的状态十分少。

　　因此可以像UVa 11997那样进行优化。

　　当一个非树边序列出队时，代价和比它大的才可能有用。

　　因此，考虑一个非树边序列出队时通过下面的方法来进行得到新的序列:

追加操作：假如最后一条非树边的终点为$v$，找到一条起点在$v$到$t$的路径上代价最小的非树边追加在当前非树边序列后
替换操作：将最后一条非树边更换为代价比它大的1条非树边。
例如图中橙色虚线是被替换掉的非树边，紫色是新加入的非树边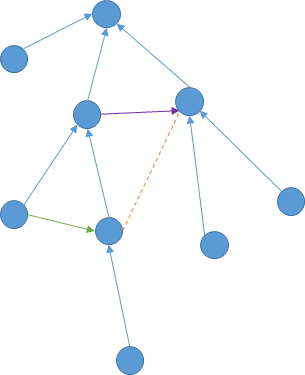

　　考虑用一些可持久化数据结构（如可持久化斜可并堆，可持久化线段树，可持久化Treap）来维护起点在点$u$到根的路径上的非树边的代价。

　　对于替换操作，

如果用的可持久化堆，那么把最后一条非树边替换为它所在的堆（你从哪个堆把它拿出来的）中它的左右子节点代表的边。
如果用的可持久化平衡树，那么把最后一条非树边直接替换为它的后继
......

　　这是一个很稳定的算法，时间复杂度$O\left ( n + m\log m + k\log k \right )$。就是常数有点大，sad.....

　　注意一些细节

计算代价时需要考虑终点是否可以到达$t$
考虑$s = t$时，要求的$k$短路包不包含0
$k$短路不存在，队首为空

（注意！不能用斜堆可持久化，斜堆的时间复杂度是均摊的。这里能过应该只是没有被卡）

Code

 /**

  * poj

  * Problem#2449

  * Accepted

  * Time: 438ms

  * Memory: 15196k

  */

 #include <algorithm>

 #include <iostream>

 #include <cstring>

 #include <cstdio>

 #include <vector>

 #include <queue>

 using namespace std;

 typedef bool boolean;

 #define pii pair<int, int>

 #define fi first

 #define sc second

 typedef class Node {

     public:

         int val, ed;

         Node *l, *r;

         Node()    {        }

         Node(int val, int ed, Node *l, Node *r):val(val), ed(ed), l(l), r(r) {        }

 }Node;

 #define Limit 1000000

 Node pool[Limit];

 Node* top = pool;

 Node* newnode(int val, int ed) {

     if(top >= pool + Limit)

         return new Node(val, ed, NULL, NULL);

     top->val = val, top->ed = ed, top->l = top->r = NULL;

     return top++;

 }

 Node* merge(Node* a, Node* b) {

     if (!a)    return b;

     if (!b)    return a;

     if (a->val > b->val)    swap(a, b);

     Node* p = newnode(a->val, a->ed);

     p->l = a->l, p->r = a->r;

     p->r = merge(p->r, b);

     swap(p->l, p->r);

     return p;

 }

 typedef class Status {

     public:

         int dist;

         Node* p;

         Status(int dist = , Node* p = NULL):dist(dist), p(p) {        }

         boolean operator < (Status b) const {

             return dist > b.dist;

         }

 }Status;

 typedef class Edge {

     public:

         int end, next, w;

         Edge(int end = , int next = , int w = ):end(end), next(next), w(w) {        }

 }Edge;

 typedef class MapManager {

     public:

         int ce;

         int* h;

         Edge* es;

         MapManager() {            }

         MapManager(int n, int m):ce() {

             h = new int[(n + )];

             es = new Edge[(m + )];

             memset(h, , sizeof(int) * (n + ));

         }

         void addEdge(int u, int v, int w) {

             es[++ce] = Edge(v, h[u], w);

             h[u] = ce;

         }

         Edge& operator [] (int pos) {

             return es[pos];

         }

 }MapManager;

 int n, m;

 int s, t, k;

 MapManager g;

 MapManager rg;

 boolean *vis;

 int* f, *lase;

 inline void init() {

     scanf("%d%d", &n, &m);

     g = MapManager(n, m);

     rg = MapManager(n, m);

     for (int i = , u, v, w; i <= m; i++) {

         scanf("%d%d%d", &u, &v, &w);

         g.addEdge(u, v, w);

         rg.addEdge(v, u, w);

     }

     scanf("%d%d%d", &s, &t, &k);

 }

 queue<int> que;

 void spfa(MapManager& g, int s) {

     vis = new boolean[(n + )];

     f = new int[(n + )];

     lase = new int[(n + )];

     memset(f, 0x7f, sizeof(int) * (n + ));

     memset(vis, false, sizeof(boolean) * (n + ));

     que.push(s);

     f[s] = , lase[s] = ;

     while (!que.empty()) {

         int e = que.front();

         que.pop();

         vis[e] = false;

         for (int i = g.h[e]; i; i = g[i].next) {

             int eu = g[i].end, w = g[i].w;

             if (f[e] + w < f[eu]) {

                 f[eu] = f[e] + w, lase[eu] = i;

                 if (!vis[eu]) {

                     vis[eu] = true;

                     que.push(eu);

                 }

             }

         }

     }

  }

 Node** hs;

 inline void rebuild() {

     for (int i = ; i <= n; i++)

         for (int j = g.h[i]; j; j = g[j].next) {

             int e = g[j].end;

             if (lase[i] != j)

                 g[j].w += f[e] - f[i];

         }

     hs = new Node*[(n + )];

     que.push(t);

     hs[t] = NULL;

     while (!que.empty()) {

         int e = que.front();

         que.pop();

         if (lase[e])

             hs[e] = hs[g[lase[e]].end];

         for (int i = g.h[e]; i; i = g[i].next)

             if (lase[e] != i && f[g[i].end] != 0x7f7f7f7f)

                 hs[e] = merge(hs[e], new Node(g[i].w, g[i].end, NULL, NULL));

         for (int i = rg.h[e]; i; i = rg[i].next) {

             int eu = rg[i].end;

             if (lase[eu] == i)

                 que.push(eu);

         }

     }

 }

 inline int kthpath(int k) {

     if (s == t)

         k++;

     if (f[s] == 0x7f7f7f7f)

         return -;

     if (k == )

         return f[s];

     priority_queue<Status> q;

     if (!hs[s])

         return -;

     q.push(Status(hs[s]->val, hs[s]));

     while (--k && !q.empty()) {

         Status e = q.top();

         q.pop();

         if(k == )

             return e.dist + f[s];

         int eu = e.p->ed;

         if (hs[eu])

             q.push(Status(e.dist + hs[eu]->val, hs[eu]));

         if (e.p->l)

             q.push(Status(e.dist - e.p->val + e.p->l->val, e.p->l));

         if (e.p->r)

             q.push(Status(e.dist - e.p->val + e.p->r->val, e.p->r));

     }

     return -;

 }

 inline void solve() {

     printf("%d\n", kthpath(k));

 }

 int main() {

     init();

     spfa(rg, t);

     rebuild();

     solve();

     return ;

 }

最短路算法+可持久化堆

特别鸣谢

　　YJQ

　　ZJC