softmax+交叉熵

1 softmax函数

softmax函数的定义为

$$softmax(x)=\frac{e^{x_i}}{\sum_j e^{x_j}} \tag{1}$$

softmax函数的特点有

• 函数值在[0-1]的范围之内
• 所有$softmax(x_i)$相加的总和为1

面对一个分类问题，能将输出的$y_i$转换成[0-1]的概率，选择最大概率的$y_i$作为分类结果^[1]。

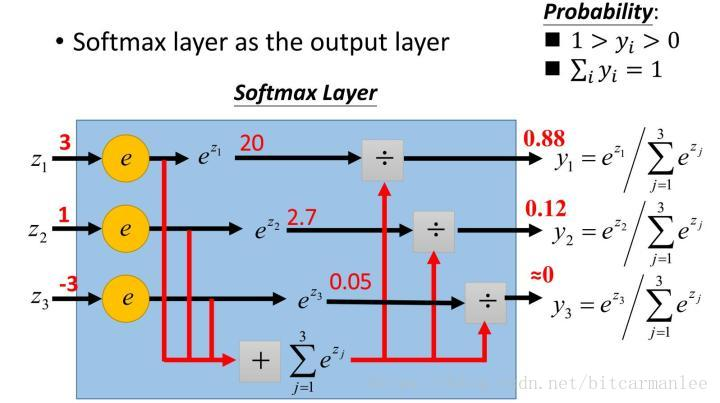
这里需要提及一个有些类似的sigmoid函数，其定义为

$$sigmoid(x)=\frac{1}{1+e^{-x_i}} \tag{2}$$

sigmoid函数将每个$y_i$都映射到[0-1]之间，但每个$y_i$之间是相互独立的，$\sum y_i$与1没有关系，可以用作二分类；而softmax函数的本质是将一个k维数据$[a_1,a_2,a_3,...,a_k]$映射成另外一个K为向量$[b_1,b_2,b_3,...,b_k]$，每个值之间是相互存在关系的^[2]，$\sum a_i=\sum b_i=1$，可以用于多分类问题，选取权重最大的一维。

下面介绍几个例子，区分softmax和sigmoid的使用场景^[1]。

如果你在开发一个音乐分类的应用，需要对k种类型的音乐进行识别，那么是选择使用 softmax 分类器呢，还是使用 logistic 回归算法建立 k 个独立的二元分类器呢？
这一选择取决于你的类别之间是否互斥，例如，如果你有四个类别的音乐，分别为：古典音乐、乡村音乐、摇滚乐和爵士乐，那么你可以假设每个训练样本只会被打上一个标签（即：一首歌只能属于这四种音乐类型的其中一种），此时你应该使用类别数 k = 4 的softmax回归。（如果在你的数据集中，有的歌曲不属于以上四类的其中任何一类，那么你可以添加一个“其他类”，并将类别数 k 设为5。）
如果你的四个类别如下：人声音乐、舞曲、影视原声、流行歌曲，那么这些类别之间并不是互斥的。例如：一首歌曲可以来源于影视原声，同时也包含人声 。这种情况下，使用4个二分类的 logistic 回归分类器更为合适。这样，对于每个新的音乐作品 ，我们的算法可以分别判断它是否属于各个类别。
现在我们来看一个计算视觉领域的例子，你的任务是将图像分到三个不同类别中。(i) 假设这三个类别分别是：室内场景、户外城区场景、户外荒野场景。你会使用sofmax回归还是 3个logistic 回归分类器呢？ (ii) 现在假设这三个类别分别是室内场景、黑白图片、包含人物的图片，你又会选择 softmax 回归还是多个 logistic 回归分类器呢？
在第一个例子中，三个类别是互斥的，因此更适于选择softmax回归分类器 。而在第二个例子中，建立三个独立的 logistic回归分类器更加合适。

因此，当label之间是互斥的，我们通常使用softmax，而当label之间是相互独立的，我们可以使用sigmoid。

2 交叉熵

2.1 信息熵

香农曾提出了一个重要的概念：信息熵，其定义为：

$$H(X)=\sum_j p(x)log(p(x)) \tag{3}$$

信息熵表示一个信息的混乱程度，信息熵越大，混乱程度越大。因此，在C4.5中就信息增益的最大值，其目的就是使一个信息的混乱程度最大化降低。

2.2 相对熵（KL散度）

从而引出相对熵（KL散度）的概念：如果我们对于同一个随机变量x有两个单独的概率分布P(x)和Q(x)，我们可以使用KL散来衡量这两个分布的差异。

其中，P往往用来表示样本的真实分布，比如[1,0,0]表示当前样本属于第一类。Q用来表示模型所预测的分布，比如[0.7,0.2,0.1]。直观的理解就是，如果用P来描述样本，那么就非常完美；而用Q来描述样本，虽然可以大致描述，但是不是那么的完美，信息量不足，需要额外的一些”信息增量”才能达到和P一样完美的描述。如果我们的Q通过反复训练，也能完美的描述样本，那么就不再需要额外的“信息增量”，Q等价于P^[3]。

相对熵的定义为：

$$D_{K||L}(p||q)=\sum_{i=1}^{n}p(x_i)ln(\frac{p(x_i)}{q(x_i)}) \tag{4}$$

其中，$D_{K||L}$的值越小，表示q分布和p分布越接近。

2.3 交叉熵

对公式4进行变形，从而得到：

\begin{align*}
{D_{KL}}(p||q) &= \sum\limits_{i = 1}^n {p({x_{_i}})\ln (p({x_i}))} - \sum\limits_{i = 1}^n {p({x_{_i}})\ln (q({x_i}))} \\
&= - H(p(x)) + [ - \sum\limits_{i = 1}^n {p({x_{_i}})\ln (q({x_i}))} ] \tag{5}
\end{align*}

等式的前一部分恰巧就是p的熵，等式的后一部分，就是交叉熵：

\begin{align*}
H(p,q) =  - \sum\limits_{i = 1}^n {p({x_{_i}})\ln (q({x_i}))}\tag{6}
\end{align*}

在机器学习中，我们需要评估label和predicts之间的差距，使用KL散度刚刚好，即${D_{KL}}(y|\hat y)$。当${D_{KL}}(y|\hat y)$越小，说明label和predicts之间的差距越小。由于KL散度中的前一部分$H(y)$不变，故在优化过程中，只需要关注交叉熵就可以了。所以一般在机器学习中直接使用交叉熵做loss，评估模型^[3]。

3 softmax+交叉熵求导

接下来，我们针对softmax模型，损失函数为交叉熵进行求导，了解其数学原理^[4]。

对公式6稍作变形，损失函数为：

\begin{align*}
L =  - \sum\limits_i {{y_i}\ln {a_i}} \tag{7}
\end{align*}

其中，$y_i$为真实分布，$a_i$而为预测分布，即softmax输出的结果。因此，softmax的定义为：

\begin{align*}
{a_i} = \sigma ({z_i}) = \frac{{{e^{{z_i}}}}}{{\sum\limits_j {{e^{{z_j}}}} }} \tag{8}
\end{align*}

\begin{align*}
{z_i} = \sum\limits_j {{w_{ij}}{x_{ij}} + b} \tag{9}
\end{align*}

其中，$z_i$为神经元的输出，如下图所示。

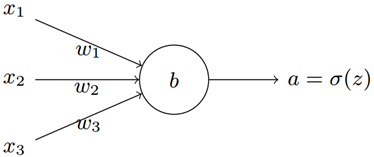
做完上面的准备后，我们需要对Loss损失函数进行求导，即$\frac{{\partial L}}{{\partial {w_i}}}$和$\frac{{\partial L}}{{\partial {b_i}}}$。根据链式法则，我们可以分解成

\begin{align*}
\frac{{\partial L}}{{\partial {w_{ij}}}} = \frac{{\partial L}}{{\partial {z_i}}}\frac{{\partial {z_i}}}{{\partial {w_{ij}}}}{\rm{ = }}\frac{{\partial L}}{{\partial {z_i}}}{x_{ij}}\\
\frac{{\partial L}}{{\partial {b_i}}} = \frac{{\partial L}}{{\partial {z_i}}}\frac{{\partial {z_i}}}{{\partial {b_i}}} = \frac{{\partial L}}{{\partial {z_i}}} \tag{10}
\end{align*}

因此，重点还是$\frac{{\partial L}}{{\partial {z_i}}}$的获取。根据链式法则：

\begin{align*}
\frac{{\partial L}}{{\partial {z_i}}} = \sum\limits_j {(\frac{{\partial {L_j}}}{{\partial {a_j}}}\frac{{\partial {a_j}}}{{\partial {z_i}}})} \tag{11}
\end{align*}

这里为什么是$a_j$而不是$a_i$呢？这里要看一下softmax的公式了，因为softmax公式的特性，它的分母包含了所有神经元的输出，所以，对于不等于i的其它输出里面，也包含着$z_i$，所有的a都要纳入到计算范围中，并且后面的计算可以看到需要分为$i=j$和i \ne j两种情况求导。

对于公式(11)中的前一项$\frac{{\partial L_j}}{{\partial {a_j}}}$可以先行求出来，得到：

\begin{align*}
\frac{{\partial {L_j}}}{{\partial {a_j}}}{\rm{ = }}\frac{{\partial ( - {y_j}\ln {a_j})}}{{\partial {a_j}}} = - {y_j}\frac{1}{{{a_j}}} \tag{12}
\end{align*}

这里值得留意的是，$L=L_1+L_2+...+L_n$，我们这里是对$L_j$进行求导。

• 当$i=j$时

\begin{align*}
\frac{{\partial {a_j}}}{{\partial {z_i}}} = \frac{{\partial {a_i}}}{{\partial {z_i}}} = \frac{{\partial \left( {\frac{{{e^{{z_i}}}}}{{\sum\nolimits_j {{e^{{z_j}}}} }}} \right)}}{{\partial {z_i}}} = \frac{{{e^{{z_i}}}\sum\nolimits_j {{e^{{z_j}}}} - {{\left( {{e^{{z_i}}}} \right)}^2}}}{{{{\left( {\sum\nolimits_j {{e^{{z_j}}}} } \right)}^2}}} = \frac{{{e^{{z_i}}}\left( {\sum\nolimits_j {{e^{{z_j}}}} - {e^{{z_i}}}} \right)}}{{{{\left( {\sum\nolimits_j {{e^{{z_j}}}} } \right)}^2}}}\\
= \frac{{{e^{{z_i}}}}}{{\sum\nolimits_j {{e^{{z_j}}}} }}\left( {1 - \frac{{{e^{{z_i}}}}}{{\sum\nolimits_j {{e^{{z_j}}}} }}} \right) = {a_i}\left( {1 - {a_i}} \right)  \tag{13}
\end{align*}

• 当$i \ne j$时

\begin{align*}
\frac{{\partial {a_j}}}{{\partial {z_i}}} = \frac{{\partial \left( {\frac{{{e^{{z_j}}}}}{{\sum\nolimits_k {{e^{{z_k}}}} }}} \right)}}{{\partial {z_i}}} = \frac{{ - {e^{{z_j}}}{e^{{z_i}}}}}{{{{\left( {\sum\nolimits_k {{e^{{z_k}}}} } \right)}^2}}} = - {a_j}{a_i} \tag{14}
\end{align*}

因此，将两种情况进行相结合

\begin{align*}
\frac{{\partial L}}{{\partial {z_i}}} &= \sum\limits_j {(\frac{{\partial {L_j}}}{{\partial {a_j}}}\frac{{\partial {a_j}}}{{\partial {z_i}}})} \\
&= \sum\limits_{i = j} {(\frac{{\partial {L_j}}}{{\partial {a_j}}}\frac{{\partial {a_j}}}{{\partial {z_i}}})} + \sum\limits_{i \ne j} {(\frac{{\partial {L_j}}}{{\partial {a_j}}}\frac{{\partial {a_j}}}{{\partial {z_i}}})} \\
&= - {y_i}\frac{1}{{{a_i}}}{a_i}(1 - {a_i}) + \sum\limits_{i \ne j} {({y_j}\frac{1}{{{a_j}}}{a_j}{a_i})} \\
&= - {y_i}(1 - {a_i}) + \sum\limits_{i \ne j} {{y_j}{a_i}} \\
&= \sum\limits_{i \ne j} {{y_j}{a_i}} + {y_i}{a_i} - {y_i}\\
&= {a_i}\sum\limits_j {{y_j}} - {y_i} \tag{15}
\end{align*}

最后，针对分类问题，我们给定的结果$y_i$最终只会有一个类别是1，其他类别都是0，即$\sum_j y_j=1$，因此，对于分类问题，这个梯度等于：

\begin{align*}
\frac{{\partial L}}{{\partial {z_i}}}{\rm{ = }}{a_i} - {y_i} \tag{16}
\end{align*}

references:

[1] https://blog.csdn.net/bitcarmanlee/article/details/82320853

[2] https://www.cnblogs.com/charlesblc/p/6750290.html

[3] https://blog.csdn.net/tsyccnh/article/details/79163834

[4] https://blog.csdn.net/qian99/article/details/78046329