生成函数小结——[ EGF ][ ln 的一个套路 ][ 概率生成函数 ]

看了jcvb的WC2015交流课件。虽然没懂后面的复合逆部分，但生成函数感觉受益良多。

指数生成函数

　　集合中大小为 i 的对象的权值是 \( a_i \) ，该集合的生成函数是 \( \sum\limits_{i>=0} \frac{a_i}{i!} x^i \)

　　一个重要式子： \( \sum\limits_{i=0}^{\infty} \frac{A^i}{i!} = e^A \) 。其中 A 可以是一个多项式。

　　对于有标号对象的计数。可以“拼接”，即 “大小为 i 的集合的带标号方案” 与 “大小为 j 的集合的带标号方案” ，想要维持相对大小地拼在一起变成 “大小为 i+j 的集合的带标号方案”。

　　“拼接” 的方法就是直接把两个 EGF 乘在一起。

　　一般来说，要取出 “有 n 个元素” 的方案，就是把 \( x^n \) 系数拿出来，乘上 n! 。这样就表示了组合数（因为集合的相对顺序无关，所以是组合数）。

　　但在 “拼接” 的过程中，不用担心 n! 的部分，直接把只有 \( \frac{1}{i!} \) 和 \( \frac{1}{j!} \) 的部分乘起来，就是正确的。

　　比如课件中举的例子：

　　

　　\( 2^{\binom{n}{2}} \) 是 n 个点的简单无向图的方案数。直接乘了一个 \( \frac{1}{n!} \) ，只看系数的话，是莫名其妙的东西。但是把 \( c_n \) 也乘上 \( \frac{1}{n!} \) 作为 EGF 的系数，两者就可以直接 “拼接” 。最后的答案就是 \( C(x) \) 的 \( x^n \) 项系数再乘一个 \( n! \) 。

多项式 ln 相关

　　一个重要式子： \( \sum\limits_{i>=1} \frac{x^i}{i} = -ln(1-x) \)

　　更普遍的形式其实是： \( ln(1+x) = \sum\limits_{i>=1}\frac{(-1)^{i-1}}{i} x^i \)

　　与之相关的应用，这里举出课件上涉及的两个：

　　1.置换计数

　　　　轮换组成置换，适合用 EGF 的角度来看。

　　最后那步就是 \( exp(-ln(1-x)) = exp(ln(\frac{1}{1-x})) = \frac{1}{1-x} = \sum\limits_{i=0}^{\infty}x^i = \sum\limits_{i=0}^{\infty}\frac{i!}{i!}x^i \)

　　2.背包计数（无标号集合计数）

　　　　

　　　　课件给出了三个版本的问题，并给出了第一个版本的解答。第二个版本就是自己写的，可能有错误，欢迎指正。第三个版本不太会……

　　　　

　　　　　　不同种类算多种方案。

　　　　　　写出生成函数：\( \prod\limits_{i=1}^{n} ( \sum\limits_{j>=0}( x^{i*j} )^{a_i} \)

　　　　　　　　　　　　　\(=\prod\limits_{i=1}^{n} ( \frac{1}{1-x^i} )^{a_i} \)

　　　　　　　　　　　　　\(=exp( \sum\limits_{i=1}^{n} -a_i * ln( 1-x^i ) ) \)

　　　　　　　　　　　　　\(=exp( \sum\limits_{i=1}^{n}a_i \sum\limits_{j>=1}\frac{x^{i*j}}{j} ) \) （这里用了那个式子）

　　　　　　　　　　　　　\(=exp( \sum\limits_{j>=1} \frac{1}{j} \sum\limits_{i=1}^{n} a_i * x^{i*j} ) \)

　　　　　　　　　　　　　\(=exp( \sum\limits_{j>=1} \frac{1}{j} A(x^j) ) \)

　　　　　　对于每个 j ， A(x) 只有 j 的倍数次项的系数需要关注。复杂度可以做到调和级数 nlogn 。

　　　　

　　　　　　写出生成函数：\( \prod\limits_{i=1}^{n} ( 1+x^i )^{a_i} \)

　　　　　　　　　　　　　\(=exp( \sum\limits_{i=1}^{n} a_i * ln(1+x^i) ) \)

　　　　　　　　　　　　　\(=exp( \sum\limits_{i=1}^{n} a_i \sum\limits_{j>=1} \frac{(-1)^{j-1}}{j} x^{i*j} ) \)

　　　　　　　　　　　　　\(=exp( \sum\limits_{j>=1} \frac{(-1)^{j-1}}{j} A(x^j) ) \)

　　　　

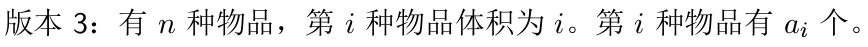
　　　　　　写出生成函数：\( \prod\limits_{i=1}^{n} \sum\limits_{j=0}^{a_i} x^{i*j} \)

　　　　　　　　　　　　　\(=exp( \sum\limits_{i=1}^{n} ln( \frac{1-x^{j*(a_i+1)}}{1-x^i} ) ) \)

　　　　　　然后就不会了……

　　　　这种背包计数的题，遇见两道，把自己的博客链接粘过来：

　　　　https://www.cnblogs.com/Narh/p/10396644.html

　　　　https://www.cnblogs.com/Narh/p/10405656.html

　　　　当初做这两个题的时候，用的是另一个式子来推导的：\( ( ln( f(x) ) )' = \frac{f'(x)}{f(x)} \)

　　　　写成那样，分子就用多项式的样子写求导，即把指数搬下来；分母就是正常的式子，和分子乘一下，整个就变成一个好看的多项式的样子了。

　　　　然后积分也是用多项式的样子写，把系数搬到指数上，推出来的结果就是一样的。

　　　　不过不管是这个式子，还是这回介绍的那个式子，都不太明白为什么能这样等于过去……

看了yml的2018集训队论文，学习了一下概率生成函数。不过没懂方差那部分。

概率生成函数

　　概率生成函数就是以 “离散变量 x = i 的概率” 为第 i 项系数的生成函数。

　　考虑论文里涉及的三道例题。

　　一. CTSC2006 歌唱王国

　　　　题目：https://www.luogu.org/problemnew/show/P4548

　　　　令 F(x) 表示序列在第 i 个位置结尾的概率。 G(x) 表示序列在第 i 个位置没有结尾的概率（的普通生成函数）。

　　　　列方程：

　　　　　　　　\( F(x)+G(x) = 1+G(x)*x \)

　　　　　　　　左边是第 i 个位置随便的方案。右边是第 i-1 个位置没有结尾，然后又填一个字符的方案。那么第 i 个位置就也是随便的。+1表示第 0 个位置，因为该位置没有 “第 i-1 个位置”。

　　　　　　　　\( G(x)(\frac{1}{m}x)^L = \sum\limits_{i=1}^{L}a_i F(x) (\frac{1}{m}x)^{L-i} \)

　　　　　　　　其中， \( a_i \) 表示 [ A[ 1,i ] = A[ len-i+1 , len ] ] ，（A是特定序列）。

　　　　　　　　左边表示给第 i 个位置后面接上那个特定序列。这样它一定结束了。考察这 L 个接上的位置，发现在 L 的中间也可能已经结束。

　　　　　　　　假如接了 i 个字符就结束，那么自己刚才填的是特定序列的前 i 个字符，结束表示这 i 个字符也是特定序列的后 i 个字符。所以有右边的式子。

　　　　第一个方程，两边求导（(a+b)' = a' + b'），得到 \( F'(x)+G'(x) = G'(x)*x + G(x) \)

　　　　因为要求的是 F'(1) ，所以把两个式子的 x 都代入 1 ，得到

　　　　　　　　\( F'(1) = G(1) \)

　　　　　　　　\( G(1) = \sum\limits_{i=1}^{L} a_i F(1) m^i \) （把左边的 \( (\frac{1}{m}x)^L \) 放到右边）

　　　　又有 F(1)=1 ，所以 \( F'(1) = \sum\limits_{i=1}^{L} a_i m^i \)

　　　　那个 \( F'(1) = G(1) \) ，有 “ 长度的期望 = \( \sum\limits_{i=0}^{\infty} \) 在 i 处没有结尾的概率 ” 这样的理解。

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int rdn()
{
  int ret=;bool fx=;char ch=getchar();
  while(ch>''||ch<''){if(ch=='-')fx=;ch=getchar();}
  while(ch>=''&&ch<='')ret=ret*+ch-'',ch=getchar();
  return fx?ret:-ret;
}
const int N=1e5+,mod=1e4;
int n,m,a[N],nxt[N],bin[N];
int main()
{
  m=rdn(); n=1e5;bin[]=;
  for(int i=;i<=n;i++)
    bin[i]=bin[i-]*m%mod;
  int T=rdn();
  while(T--)
    {
      n=rdn();for(int i=;i<=n;i++)a[i]=rdn();
      for(int i=;i<=n;i++)
    {
      int cr=nxt[i-];
      while(cr&&a[cr+]!=a[i])cr=nxt[cr];
      if(a[cr+]==a[i])nxt[i]=cr+;
      else nxt[i]=;
    }
      int cr=nxt[n], ans=bin[n];
      while(cr)
    {
      ans=(ans+bin[cr])%mod; cr=nxt[cr];
    }
      printf("%04d\n",ans);
    }
  return ;
}

　　二. SDOI2017 硬币游戏

　　　　题目：https://www.luogu.org/problemnew/show/P3706

　　　　令 \( F_j(x) \) 表示 i 位置，用串 j 结尾的概率生成函数。 G(x) 表示 i 位置还没结尾的概率。

　　　　用理解列式子： \( \sum\limits_{k=1}^{n} F_k(1) = 1 \) （用求导的那个方法推，也是一样）

　　　　又有，对于第 k 个串： \( G(x)(\frac{1}{2}x)^{L_k} = \sum\limits_{i=1}^{L_k} \sum\limits_{j=1}^{n} a_{k,j,i} ( \frac{1}{2}x )^{L_k -i} \)

　　　　　　　　其中， \( a_{k,j,k} \) 表示 [ k 串的 i 长度前缀 = j 串的 i 长度后缀 ] 。

　　　　即 \( G(1) = \sum\limits_{i=1}^{L_k} \sum\limits_{j=1}^{n} a_{k,j,i} 2^i f_j(1) \)

　　　　其实这样就可以高斯消元了！

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define ll long long
#define db double
using namespace std;
const int N=,b1=,m1=1e9+,b2=,m2=;
int upt1(int x){while(x>=m1)x-=m1;while(x<)x+=m1;return x;}
int upt2(int x){while(x>=m2)x-=m2;while(x<)x+=m2;return x;}

int n,m,bn1[N],bn2[N],h1[N][N],h2[N][N];
db bin[N],a[N][N],f[N]; char s[N];
pair<int,int> get_h(int x,int l)
{
  int a=upt1(h1[x][m]-(ll)bn1[m-l+]*h1[x][l-]%m1);
  int b=upt2(h2[x][m]-(ll)bn2[m-l+]*h2[x][l-]%m2);
  return make_pair(a,b);
}
void gauss(int n)
{
  for(int i=;i<=n;i++)
    {
      int cr=i;
      for(int j=i+;j<=n;j++)
    if(fabs(a[j][i])>fabs(a[cr][i]))cr=j;
      //if(!a[cr][i])break;
      for(int j=i;j<=n+;j++)swap(a[i][j],a[cr][j]);
      for(int j=i+;j<=n;j++)
    {
      db sl=a[j][i]/a[i][i];
      for(int k=i;k<=n+;k++) a[j][k]-=sl*a[i][k];
    }
    }
  for(int i=n;i;i--)
    {
      f[i]=a[i][n+]/a[i][i];//// /a[i][i]
      for(int j=i-;j;j--) a[j][n+]-=f[i]*a[j][i];
    }
}
int main()
{
  scanf("%d%d",&n,&m);
  bn1[]=bn2[]=;
  for(int i=;i<=m;i++)bn1[i]=(ll)bn1[i-]*b1%m1;
  for(int i=;i<=m;i++)bn2[i]=(ll)bn2[i-]*b2%m2;
  for(int i=;i<=n;i++)
    {
      scanf("%s",s+);
      for(int j=;j<=m;j++)
    {
      int w; if(s[j]=='H')w=; else w=;
      h1[i][j]=((ll)h1[i][j-]*b1+w)%m1;
      h2[i][j]=((ll)h2[i][j-]*b2+w)%m2;
    }
    }
  bin[]=;for(int i=;i<=m;i++)bin[i]=bin[i-]*;
  for(int k=;k<=n;k++)
    {
      for(int j=;j<=n;j++)
    for(int i=;i<=m;i++)
      if(make_pair(h1[k][i],h2[k][i])==get_h(j,m-i+))
        a[k][j]+=bin[i];
      a[k][n+]=-;//G(1)
    }
  for(int i=;i<=n;i++)a[n+][i]=; a[n+][n+]=;
  gauss(n+);
  for(int i=;i<=n;i++)printf("%.10f\n",f[i]);
  return ;
}

　　　　关于本题的另一种想法：https://www.cnblogs.com/Narh/p/10407245.html

　　三. Dice

　　　　题目：http://acm.hdu.edu.cn/showproblem.php?pid=4652

　　　　题意：m 面的骰子。求：1.期望多少次，可以使得 “最后 n 次投出来的结果相同” ；2.期望多少次，可以是的 “最后 n ( n<=m ) 次投出来的结果互不相同” 。

　　　　对于第一问，令 \( F_j(x) \) 表示以第 j 面重复 n 次结束的概率，\( G(x) \) 表示不结束的概率。

　　　　　　所有面等价，所以 \( \sum F_j(1) = 1  ==>  F_j(1) = \frac{1}{m} \)

　　　　　　又有 \( \sum F'_j(1) = G(1) \) ， \( G(1) \) 就是答案。

　　　　　　\( G(x)( \frac{1}{m}x )^n = \sum\limits_{i=1}^{n} F_k(x) ( \frac{1}{m}x )^{L-i} \) ，其中 k 是某一面。

　　　　　　\( ==> G(1) = \sum\limits_{i=1}^{n} F_k(x) m^i = \sum\limits_{i=1}^{n} \frac{1}{m}*m^i = \sum\limits_{i=0}^{n} m^i \)

　　　　对于第二问，有 \( ( tot= \binom{m}{n}*n! = \frac{m!}{(m-n)!} ) \) 种结尾。令 \( F_j(x) \) 表示以第 j 种结尾结束的概率， \( G(x) \) 表示不结束的概率。

　　　　　　所有结尾等价，所以 \( \sum F_j(1) = 1 ==> F_j(1) = \frac{(m-n)!}{m!} \)

　　　　　　又有 \( \sum F'_j(1) = G(1) \) ， \( G(1) \) 就是答案。

　　　　　　\( G(x)(\frac{1}{m}x)^n = \sum\limits_{i=1}^{n} \sum\limits_{j=1}^{tot} a_{k,j,i} F_j(x) (\frac{1}{m}x)^{n-i} \)

　　　　　　　　其中， \( a_{k,j,i} \) 表示 [ 第 k 个结尾的前 i 个字符 == 第 j 个结尾的后 i 个字符 ] 。

　　　　　　\( G(1) = \sum\limits_{i=1}^{n} \frac{(m-n)!}{m!} * m^i \sum\limits_{j=1}^{tot} a_{k,j,i} \)

　　　　　　　　其实 \( \sum\limits_{j=1}^{tot} a_{k,j,i} \) 是能算的。已知 i 个位置相等，剩下位置的方案就是 \( \binom{m-i}{n-i} * (n-i)! = \frac{(m-i)!}{(m-n)!} \)

　　　　　　\( G(1) = \sum\limits_{i=1}^{n} \frac{(m-i)!}{m!}*m^i = \sum\limits_{i=1}^{n} \frac{m^i}{m的i次下降幂} \)

#include<cstdio>
#include<cstring>
#include<algorithm>
#define db double
using namespace std;
const int N=1e6+;
int op,n,m;
int main()
{
  int T; scanf("%d",&T);
  while(T--)
    {
      scanf("%d%d%d",&op,&m,&n);
      if(!op)
    {
      int ml=,ans=;
      for(int i=;i<n;i++)
        { ans+=ml; if(i<n-)ml*=m;}
      printf("%d\n",ans);
    }
      else
    {
      db ans=,ml=;
      for(int i=,j=m;i<=n;i++,j--)
        { ml=ml/j*m; ans+=ml;}
      printf("%.10f\n",ans);
    }
    }
  return ;
}