C++笔记（5）——浮点数的比较

判断是否相等

因为一个浮点数的存储并不总是精确的，例如在经过大量计算之后可能会将3.14保存为3.1400000000001或者3.1439999999999，这时候如果直接用==来比较这两个数的话会输出错误的结果，false（C++中==只有在两个数字完全相同的情况下才判定为true）。所以需要引入极小数eps来修正，只要不超出这个误差，那么就判定为true。

通常定义一个eps为常量1e-8:

const double eps = 1e-8;

对应的定义判定是否相等的操作Equ：

#define Equ(a, b) ((fabs((a)-(b))<(eps))

上面这行代码是通过宏定义来定义出一个名为Equ的函数，这个函数会将a和b相减，如果相差的结果的绝对值小于极小值eps，那么就判定为true，否则为false。上面加这么多括号是为了防止宏定义可能带来的错误，不能够省略掉。相对应的，如果需要使用不等于，那么只需要用!Equ(a, b)即可。

使用上述函数的例子：

#include <stdio.h>
#include <math.h>

const double eps = 1e-8;
#define Equ(a,b) ((fabs((a) - (b)) < (eps))

int main(){
    double db = 1.23;
    if(Equ(db, 1.23)){
        printf("equal");
    }
    else{
        printf("not equal")
    }
    return 0;
}

大于

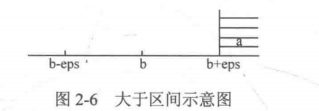
#define More(a,b) (((a) - (b)) > (eps))

小于

#define Less(a,b) (((a)-(b)) < (-eps))

大于等于

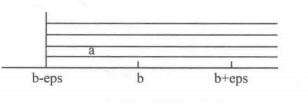
#define MoreEqu(a,b) (((a)-(b))>(-eps))

小于等于

#define LessEqu(a,b) (((a)-(b))<(eps))

补充：圆周率

\(\cos{\pi} = -1\), \(\pi = \arccos{-1}\)，所以：

const double Pi = acos(-1.0);

与误差相关的补充

另外还有：

1. 在经过大量计算后可能因为误差的累计，一个变量中存储的0实际上是一个非常小的负数，如果这时候对这个变量进行开根号操作sqrt，那么会报错（asin(x)类似，当存放的x为+1或-1时也会出现类似的情况）。因此需要用eps来保证变量在定义域内；
2. 一些编译环境下0.00的变量可能在输出时会变成-0.00。这是一个bug，只能将结果放在字符串中然后和-0.00比较，如果对比成功那么将结果加上eps来变回0.00 。

参考

《算法笔记》胡凡著