AdaGrad Algorithm and RMSProp
AdaGrad全称是Adaptive Gradient Algorithm,是标准Gradient Descent的又一个派生算法。标准Gradient Descent的更新公式为:
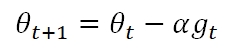
其中Learning Rate α对于Cost Function的各个feature都一样,但同一个α几乎不可能在各个feature上都表现完美,通常为了收敛,会选择较小的α。
而AdaGrad的主要思想是:在各个维度上使用不同的learning rate,从而加快函数收敛的速度。其公式为:
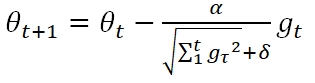
gt是t时刻目标函数的梯度,可以看到,依旧为各个feature设置了统一的α,但是通过历史梯度累计RMS作为分母来调节该learning rate。δ是一个很小的数例如10-7,仅仅为了分母不为0。
如果我们将等式右侧第二项看做一个整体。则标准Gradient Descent是,对t时刻梯度大的feature更新步子大,对t时刻梯度小的feature更新步子小。可以说Gradient Descent是衡量绝对大小的,但AdaGrad则不同,采取了“相对大与相对小”。使用当前时刻的梯度与历史梯度的RMS相比较,如果梯度变缓了,说明快要收敛了,那么步子调整的小一些;而如果梯度突然变大了,那证明参数需要大幅度更新了。
单AdaGrad算法虽然在凸函数(Convex Functions)上表现较好,但在非凸函数上却可能有局限。在深度学习训练中,Cost Function有可能会是很复杂的空间结构,有可能在某些平缓的结构上使用了很小的steps,但在某一时刻却有希望增大步伐。但上式的分母表示,优化的更新步伐和t时刻之前的所有时刻的梯度都相关,所以很有可能当算法希望增大步伐时,更新幅度已经衰减到很小,从而导致优化过程被困在某个局部最优点。
基于此,多大的Hinton教授提出了RMSProp,将AdaGrad和EMA结合起来。将上式分母的部分做成滑动的窗口,通过参数ρ来控制窗口的大小。从而,梯度的“相对大小”参照物,会丢弃遥远的历史,只与相邻窗口内的结构进行比较,来决定更新步幅的大小。梯度的EMA等于:
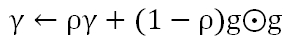
参数更新公式为:
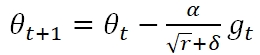
AdaGrad Algorithm and RMSProp的更多相关文章
- L21 Momentum RMSProp等优化方法
airfoil4755 下载 链接:https://pan.baidu.com/s/1YEtNjJ0_G9eeH6A6vHXhnA 提取码:dwjq 11.6 Momentum 在 Section 1 ...
- (转)分布式深度学习系统构建 简介 Distributed Deep Learning
HOME ABOUT CONTACT SUBSCRIBE VIA RSS DEEP LEARNING FOR ENTERPRISE Distributed Deep Learning, Part ...
- (转) An overview of gradient descent optimization algorithms
An overview of gradient descent optimization algorithms Table of contents: Gradient descent variants ...
- 第三十七节、人脸检测MTCNN和人脸识别Facenet(附源码)
在说到人脸检测我们首先会想到利用Harr特征提取和Adaboost分类器进行人脸检测(有兴趣的可以去一看这篇博客第九节.人脸检测之Haar分类器),其检测效果也是不错的,但是目前人脸检测的应用场景逐渐 ...
- An overview of gradient descent optimization algorithms
原文地址:An overview of gradient descent optimization algorithms An overview of gradient descent optimiz ...
- 基于MNIST数据的卷积神经网络CNN
基于tensorflow使用CNN识别MNIST 参数数量:第一个卷积层5x5x1x32=800个参数,第二个卷积层5x5x32x64=51200个参数,第三个全连接层7x7x64x1024=3211 ...
- Momentum
11.6 Momentum 在 Section 11.4 中,我们提到,目标函数有关自变量的梯度代表了目标函数在自变量当前位置下降最快的方向.因此,梯度下降也叫作最陡下降(steepest desce ...
- 第七章:网络优化与正则化(Part1)
任何数学技巧都不能弥补信息的缺失. --科尼利厄斯·兰佐斯(Cornelius Lanczos) 匈牙利数学家.物理学家 文章相关 1 第七章:网络优化与正则化(Part1) 2 第七章:网络优化与正 ...
- RNN 入门教程 Part 4 – 实现 RNN-LSTM 和 GRU 模型
转载 - Recurrent Neural Network Tutorial, Part 4 – Implementing a GRU/LSTM RNN with Python and Theano ...
随机推荐
- HDU2188选拔自愿者
悼念512汶川大地震遇难同胞--选拔志愿者 Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Ot ...
- java反射, 不看你可别后悔
开发中, 难免遇到些私有的属性和方法, 就好比下面的实体一样, 我们该怎么获得她, 并玩弄于手掌呢? 我们先来个实体瞧瞧, 给你个对象你也new不了, hahaha- 单身wang public cl ...
- Flutter 初探 -
flutter 安装 经过许久的关注,及最近google算是真正地推行flutter时,加上掘金小册也有相应的教程,我知道自己得跟着这一波潮流学习了,不然迟早会面临着小程序的危(大家都会了就你不会), ...
- C# 中File和FileStream的用法
原文:https://blog.csdn.net/qq_41209575/article/details/89178020 1.首先先介绍File类和FileStream文件流 1.1 File类, ...
- http请求报文格式(请求行、请求头、空行 和 请求包体)和响应报文格式(状态行、响应头部、空行 和 响应包体)
转载 出处 超文本传输协议(Hypertext Transfer Protocol,简称HTTP)是应用层协议.HTTP 是一种请求/响应式的协议,即一个客户端与服务器建立连接后,向服务器发送一个请求 ...
- 从excel表中生成批量SQL
excel表格中有许多数据,需要将数据导入数据库中,又不能一个一个手工录入,可以生成SQL,来批量操作. ="insert into Log_loginUser (LogID, Logi ...
- 如果存在这个表,则删除这个表的sql
mysql: drop table if exists address_book sqlserver2005:IF EXISTS (SELECT * FROM sys.objects WHERE ob ...
- 利用C51单片机模拟SPI进行双机通信
SPI协议简述 SPI,是英语Serial Peripheral interface的缩写,顾名思义就是串行外围设备接口.由Motorola首创.SPI接口主要应用在 EEPROM,FLASH,实时时 ...
- java中的Excel导出功能
public void exportExcel(Long activityId, HttpServletResponse response) throws IOException { // 获取统计报 ...
- Sass-@extend
Sass 中的 @extend 是用来扩展选择器或占位符.比如: .error { border: 1px #f00; background-color: #fdd; } .error.intrusi ...
