学习：多项式算法----FFT

FFT，即快速傅里叶变换，是离散傅里叶变换的快速方法，可以在很低复杂度内解决多项式乘积的问题（两个序列的卷积）

卷积

---

卷积通俗来说就一个公式（本人觉得卷积不重要）

$$C_k=\sum_{i+j=k}A_i*B_i$$

那么这个表达式是啥意思了：

　　有两个序列A和B，其中$A=\left\{A_1,A_2,...\right\}，B=\left\{B_1,B_2,...\right\}$

　　A序列有a个元素，B序列有b个元素。于是，由这两个序列可以推出另一个序列C，C序列如何确定了？确定方法就按照卷积的公式得来的，即$$C=\left\{\sum_{i+k=0}A_i*B_j\,,\,\sum_{i+k=1}A_i*B_j\,,...,\sum_{i+k=2^a+2^b}A_i*B_j\right\}$$

这里只介绍一下卷积，下面来探究卷积和多项式之间的关系。

---

多项式（预备知识）

---

多项式的定义

形如

$$f(x)=a_0+a_1x+a_2x^2+...+a_nx^n$$

的函数关系式叫做关于x的多项式，其中多项式系数可以构成一个序列，即

$$A=\left\{a_0,a_1,a_2,...,a_n\right\}$$

多项式乘法与序列的卷积

假如有两个多项式，其中

$f(x)=a_0+a_1x+a_2x^2+...+a_nx^n$

$g(x)=b_0+b_1x+b_2x^2+...+b_mx^m$

现在要求f(x)*g(x)的序列，很明显

$$f(x)*g(x)=\sum_{i+j=0}a_i*b_j+\sum_{i+j=1}a_i*b_jx+\sum_{i+j=2}a_i*b_jx^2+...+\sum_{i+j=m+n}a_i*b_jx^{m+n}$$

现在把$f(x),g(x)$以及$f(x)*g(x)$三个多项式的系数拿出来写成三个序列，可得:

$A=\left\{a_0,a_1,a_2,...a_n\right\}$

$B=\left\{b_0,b_1,b_2,...b_m\right\}$

$C=\left\{\sum_{i+j=0}a_i*b_j,\sum_{i+j=1}a_i*b_j,\sum_{i+j=2}a_i*b_j,...\sum_{i+j=m+n}a_i*b_j\right\}$

于是惊讶的发现，两个序列的卷积相当于两个多项式乘积后得到的多项式的系数序列。而FFT算法的目的，就是求两个多项式乘积后得到的多项式的系数序列。

多项式的表示方法

多项式有两种表示方法，即系数表示法和点值表示法。

1.系数表示法是我们常用的表示方法，即

$$f(x)=a_0+a_1x+a_2x^2+...+a_nx^n$$

的形式

2.点值表示法，顾名思义，就是在这个多项式上任意选取不重复的n+1个点，即

$$f(x)=\left\{(x_0,y_0),(x_1,y_1),...,(x_2,y_2)\right\}$$

可以证明：任何n+1个点可以确定唯一一个最高次项为n次方的多项式（下面是证明，可以看看，也可以忽略）

将一个多项式的系数写成一个系数矩阵（当然，这些系数我们是不知道的）

$$\begin{bmatrix}a_0\\a_1\\a_2\\\vdots\\a_n\end{bmatrix}$$

然后将刚刚选取的n+1个点写成下面两个矩阵

$$\begin{bmatrix}1&x_0&x_0^2&x_0^3&\cdots&x_0^n\\1&x_1&x_1^2&x_1^3&\cdots&x_1^n\\1&x_2&x_2^2&x_2^3&\cdots&x_2^n\\\vdots&\vdots&\vdots&\vdots&\ddots&\vdots\\1&x_n&x_n^2&x_n^3&\cdots&x_n^n\end{bmatrix}\;\begin{bmatrix}y_0\\y_1\\y_2\\\vdots\\y_n\end{bmatrix}$$

可以得出以下三个矩阵的关系

$$\begin{bmatrix}1&x_0&x_0^2&x_0^3&\cdots&x_0^n\\1&x_1&x_1^2&x_1^3&\cdots&x_1^n\\1&x_2&x_2^2&x_2^3&\cdots&x_2^n\\\vdots&\vdots&\vdots&\vdots&\ddots&\vdots\\1&x_n&x_n^2&x_n^3&\cdots&x_n^n\end{bmatrix}\;\begin{bmatrix}a_0\\a_1\\a_2\\\vdots\\a_n\end{bmatrix}=\begin{bmatrix}y_0\\y_1\\y_2\\\vdots\\y_n\end{bmatrix}$$

解出系数矩阵

$$\begin{bmatrix}a_0\\a_1\\a_2\\\vdots\\a_n\end{bmatrix}=\begin{bmatrix}1&x_0&x_0^2&x_0^3&\cdots&x_0^n\\1&x_1&x_1^2&x_1^3&\cdots&x_1^n\\1&x_2&x_2^2&x_2^3&\cdots&x_2^n\\\vdots&\vdots&\vdots&\vdots&\ddots&\vdots\\1&x_n&x_n^2&x_n^3&\cdots&x_n^n\end{bmatrix}^{-1}\begin{bmatrix}y_0\\y_1\\y_2\\\vdots\\y_n\end{bmatrix}$$

只能唯一确定一个系数矩阵，即只能唯一确定一组系数，即只能唯一确定一个多项式，证明完毕

多项式乘法与FFT算法

为了实现多项式乘法并得到系数序列，我们可以考虑实现的方法，如果直接暴力（通过定义直接算系数）是O(n²)复杂度，肯定会超时，于是我们这样考虑

首先可以选取n+1个点，把两个多项式转化为点值表示法。

然后将两个点值表示法的多项式相乘（复杂度为O(n)）,然后将新得到的多项式的点值表示法转化为系数表示法。

注意：假设f(x)最高有n次方，g(x)最高有m次方，所以f(x)*g(x)最高有m+n次方，但是m+n可能不是2的幂次方，如果不是，则需要选取点的数量应该是大于m+n的2的幂次方个，假设这个值为1<<k，所以从系数表示法到点值表示法的转化过程中，我们要在f(x)和g(x)内选择1<<k的点，才能保证点值表示法的f(x)和g(x)之后，至少仍有m+n个点，才能确定唯一一个f(x)*g(x)的多项式。所以在选取点的数量的时候，要保证点的个数能确定f(x)*g(x)后的多项式。

如果任意的选取n+m个点然后转化，复杂度还是太高，所以我们需要巧妙的选取1<<k个点，从而使得系数表示法与点值表示法之间转化的复杂度降为O(nlogn)，这就是FFT算法。

---

虚数的乘积及其表示（预备知识）

---

一个虚数，是由实部和虚部组成，表示为$(a+bi)$，虚数的几何表示可以在坐标系中体现，如下图所示

如图所示，$r$为此虚数的模长，$\theta$为此虚数的幅角，于是虚数还能表示为$r(cos\theta,isin\theta)$的形式

若$z_1=r_1(cos\theta_1,isin\theta_1),z_2=r_2(cos\theta_2,isin\theta_2)$

于是$$z_1*z_2=r_1(cos\theta_1,isin\theta_1)*r_2(cos\theta_2,isin\theta_2)=r_1r_2(cos(\theta_1+\theta_2),isin(\theta_1+\theta_2))$$

可以得到虚数相乘的几何意义：模长相乘，幅角相加

---

n次单位根（预备知识）

---

定义

n次单位根$w_n$，即$x^n=1$在虚数范围内的解，即$w_n^n=1$，故n次单位根$w_n$也是一个复数，且模长为1，所以n次单位根在乘方的时候模长不变，幅角等差增大

如图所示，将一个单位圆分成n块，幅角为正且最小的那个虚数即为n次单位根（$w_n^1$，红色点），下图是n=8的情况

还要注意，$w_n^0=w_n^n=1$

由图及n次单位根的性质（n次单位根模长为1，幅角为$\frac{2\pi}{n}$）可得

$$w_n^k=cos\frac{2k\pi}{n}+i\,sin\frac{2k\pi}{n}$$

性质

比较简单的性质：

1.$w_n^{m+n}=w_n^m*w_n^n=w_n^m$

2.$(w_n^m)^n=(w_n^n)^m=1,m\in [0,n-1]$

比较复杂（重要）的性质：

1.$w_{2n}^{2k}=w_n^k$，如图所示

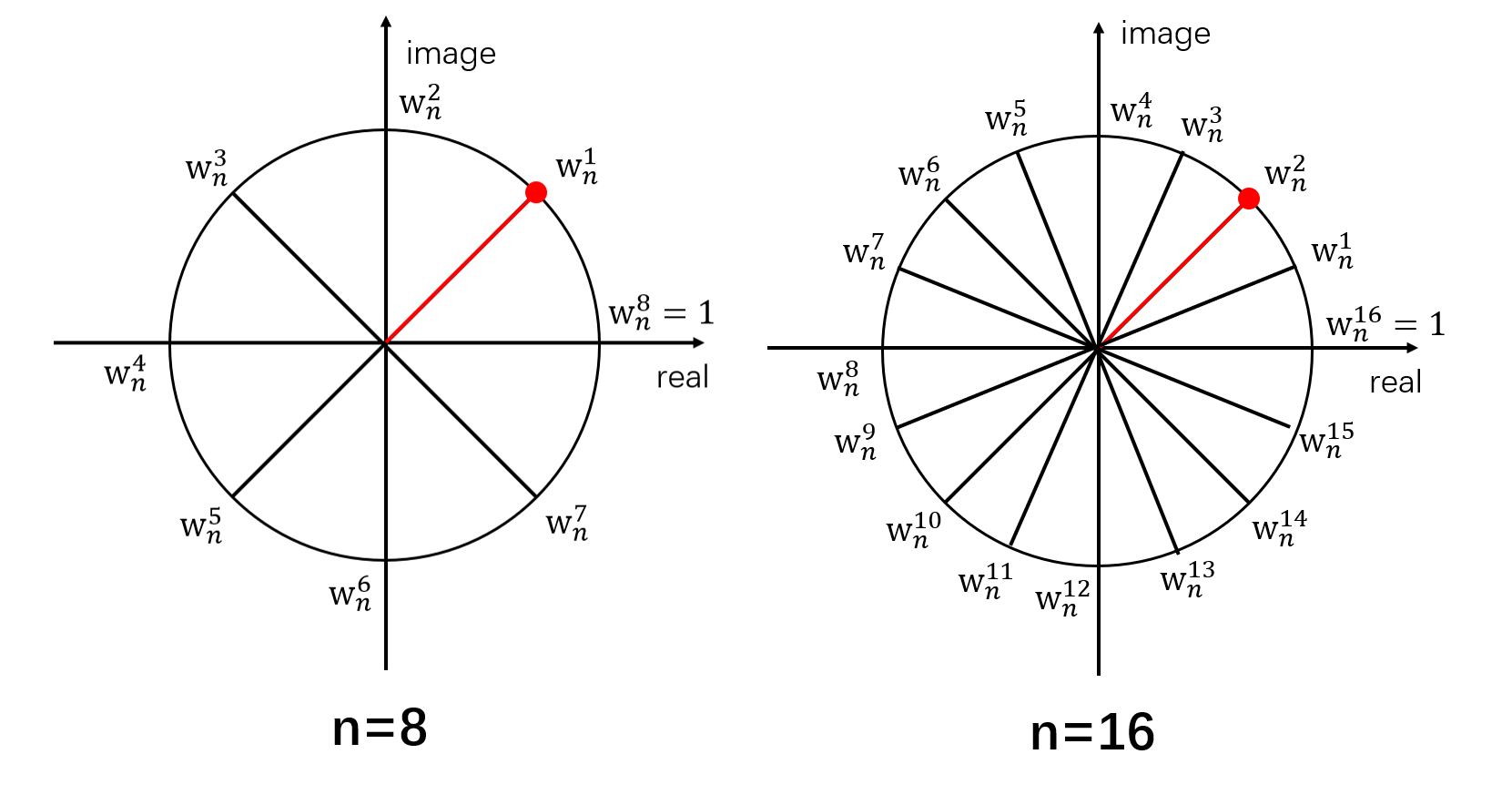
2.$w_n^k=-w_n^{k+\frac n{2}}$

通过上面那个图也可以看出来，注意一点：虚数乘-1，那么虚数的实部与虚部都要乘上-1，所以$-w_n^k$在单位圆上的点和$w_n^k$在单位圆上的点关于原点对称

3.$(w_n^k)^2=w_{\frac n{2}}^k$

推导:$(w_n^k)^2=(-w_n^{k+\frac n{2}})^2=w_n^{2*k}=w_{\frac n{2}}^k$

更加复杂（重要）的性质

$$\sum_{k=0}^{n-1}w_n^{ik}=\begin{cases} 0 & i\bmod n \ne 0 \\ n & i\bmod n=0 \end{cases}$$

证明：

　　当$i\bmod n \ne 0$时，相当如等比数列前n项和求和，故$$\sum_{k=0}^{n-1}w_n^{ik}=\frac {w_n^0(1-(w_n^i)^n)}{1-w_n^i}=\frac {1-(w_n^n)^i}{1-w_n^i}=0$$

　　当$i\bmod n = 0$时，$w_n^{ik}=1$，故$$\sum_{k=0}^{n-1}w_n^{ik}=n*1=n$$

至此，你应该知道，多项式从系数表示法转化为点值表示法时，选取的n个点的x值即为n次单位根序列$\left\{w_n^0,w_n^1,....,w_n^{n-1}\right\}$

注意，此处的n是f(x)*g(x)的多项式最高次项的次数，不是f(x)或者g(x)最高此项的系数，前面（多项式乘法与FFT）讲过要选取1<<k（再次强调这个值比f(x)*g(x)的多项式最高次的次数m+n还要大，且是2的幂次方）个点

---

FFT

---

假设现在多项式为

$f(x)=a_0+a_1x+a_2x^2+...+a_{k-1}x^{k-1}$，注意，多项式最高次项为k-1次方，共k项，k如果不等于2的n次幂，就凑成2的n次幂（加系数为0的项）

$g(x)=b_0+b_1x+b_2x^2+...+b_{h-1}x^{h-1}$，注意，多项式最高次项为h-1次方，共h项，h如果不等于2的n次幂，就凑成2的n次幂（加系数为0的项）

那么现在，我们从多项式中选取了这样一些点

${(w_n^0,f(w_n^0)),(w_n^1,f(w_n^1)),(w_n^2,f(w_n^2)),...,(w_n^{n-1},f(w_n^{n-1}))}$，共n个点

注意n是大于k+h的最小2次幂，而不是等于k+h！！！！！

此时选取得点数n大于k+h，故可以确定f(x)*g(x)这个多项式，现在，只需确定$f(w_n^0),f(w_n^1),...,f(w_n^{n-1})$的值即可。

如何算值？我们可以观察一下$f(w_n^i)$的值$(0\le i<n)$

$f(w_n^i)=a_0+a_1w_n^i+a_2(w_n^i)^2+a_3(w_n^i)^3+...+a_{k-1}(w_n^i)^{k-1}$

$=\color{Red}{a_0+a_2(w_n^i)^2+a_4(w_n^i)^4+...+a_{k-2}(w_n^i)^{k-2}}+\color{LimeGreen}{w_n^i}\color{Blue}{(a_1+a_3(w_n^i)^2+...+a_{k-1}(w_n^i)^{k-2})}$

根据$(w_n^k)^2=w_{\frac n{2}}^k$可得

$=\color{Red}{a_0+a_2w_{\frac n{2}}^i+a_4(w_{\frac n{2}}^i)^2+...+a_{k-2}(w_{\frac n{2}}^i)^{\frac {k-2}2}}+\color{LimeGreen}{w_n^i}\color{Blue}{(a_1+a_3w_{\frac n{2}}^i+...+a_{k-1}(w_{\frac n{2}}^i)^{\frac {k-2}2})}$

$=\color{Red}{f_1(w_n^i)}+\color{LimeGreen}{w_n^i}\color{Blue}{f_2(w_n^i)}$

再算$f_1(w_n^i)$的值和$f_2(w_n^i)$的值的时候，我们又可以按照奇偶分开，像算$f(w_n^i)$一样变成两个问题

同时我们发现

$f(w_n^{i+\frac n{2}})=f(-w_n^i)$

$=\color{Red}{a_0+a_2(-w_n^i)^2+a_4(-w_n^i)^4+...+a_{k-2}(-w_n^i)^{k-2}}-\color{LimeGreen}{w_n^i}\color{Blue}{(a_1+a_3(-w_n^i)^2+...+a_{k-1}(-w_n^i)^{k-2})}$

$=\color{Red}{a_0+a_2w_{\frac n{2}}^i+a_4(w_{\frac n{2}}^i)^2+...+a_{k-2}(w_{\frac n{2}}^i)^{\frac {k-2}2}}-\color{LimeGreen}{w_n^i}\color{Blue}{(a_1+a_3w_{\frac n{2}}^i+...+a_{k-1}(w_{\frac n{2}}^i)^{\frac {k-2}2})}$

$=\color{Red}{f_1(w_n^i)}-\color{LimeGreen}{w_n^i}\color{Blue}{f_2(w_n^i)}$

又发现，如果我们要算$f(w_n^i)$的值，我们会先算$f_1(w_n^i)$和$f_2(w_n^i)$的值，但是算出$f_1(w_n^i)$和$f_2(w_n^i)$的值之后，不仅能算出$f(w_n^i)$的值，还能同时算出$f(w_n^{i+\frac n{2}})$的值

总的来说，如果n=8算出了$f(w_n^0)$的值，就算出了$f(w_n^4)$的值；算出了$f(w_n^1)$，就算出来$f(w_n^5)$的值；...；算出了$f(w_n^3)$的值，就算出了$f(w_n^7)$的1值

同理，算$f_1(w_n^i)$和$f_2(w_n^i)$的值的时候，也是算出一半，得到另一半的值------每次解决问题，都会变成解决一半问题然后直接得到另一半的答案，在解决这一半问题的时候，也变成了解决一半的一半的问题，另一半的一半的问题又被直接得到答案。

这样，就可以把$f(w_n^0),f(w_n^1),f(w_n^2),...,f(w_n^{n-1})$的值全部算出来，得到了n个点的值；同理算出$g(w_n^0),g(w_n^1),f(w_n^2),...,g(w_n^{n-1})$的值。得到了f(x)和g(x)的点值表示法，点值表示法相乘，O(n)复杂度就得到了f(x)*g(x)的点值表示法。

代码如下：

#include <complex>//c++自带复数模板
typedef complex<double> Complex;//重定义数据类型，记得要用double类型
void FFT(Complex *a,int n,int inv){
//a是你要进行变换的数组（多项式系数数组），n是数组大小，inv暂时不管，你就当做它等于1
    if(n==)    return;//如果分治后的序列大小为1，就直接返回，不用继续分治了
    int mid=n>>;//如果n不等于1，那就继续分治，mid是分治后变成两个序列的长度
    static Complex b[];//创建一个辅助用的b数组，后面体现用处
    for(int i=;i<mid;i++)    b[i]=a[*i],b[i+mid]=a[*i+];//将a数组奇数位置的值和偶数位置的值分开，b数组前mid个位置存a数组偶数位置值，后mid个位置存a数组奇数位置值
    for(int i=;i<n;i++)    a[i]=b[i];//将b数组值重新赋给a数组 

    //对分治后的两个序列（一个是a数组前mid个元素组成的序列，另一个数a数组后mid元素组成的序列） 进行FFT变换
    FFT(a,mid,inv);
    FFT(a+mid,mid,inv);

    //算出一半，得到另一半的值，a数组前mid元素相当于之前说的f1，a数组后mid元素相当于之前说的f2
    for(int i=;i<mid;i++){
        Complex com(cos(*pi*i/n),inv*sin(*pi*i/n));
        b[i]=a[i]+com*a[i+mid];b[i+mid]=a[i]-com*a[i+mid];
    }

    for(int i=;i<n;i++)    a[i]=b[i];//重新将b数组赋值给a数组
    return;
}

FFT变换（递归版）

这里再来详细解释一下，上面代码中的n值

加入开始两个序列是n次多项式和m次多项式，那么开始n值就等于大于等于$(m+n)$的最小2次幂，如下代码所示

cin>>n>>m;
int k=n+m,lim=;
while(k>>=)    lim<<=;
if(lim<n+m)    lim<<=;
FFT(a,lim,);//对a序列进行变换
FFT(b,lim,);//对b序列进行变换

此时lim值就是n的初值

强调一遍$$w_n^k=cos\frac{2k\pi}{n}+i\,sin\frac{2k\pi}{n}$$

---

FFT逆变换

---

FFT逆变换则是将点值表示法转化为系数表示法的步骤。在逆变换之前，我们已经对两个多项式系数序列进行了正变换，即

FFT(a,lim,);//正变换
FFT(b,lim,);
for(int i=0;i<lim;i++)    a[i]=a[i]*b[i];//将正变换的两个序列乘在一起，得到新的多项式的点值表示法序列。

如上所示，只要将a序列进行逆变换，就可以得到新多项式的系数序列。在FFT正变换之中，我们一直在求$f(w_n^i)$的值。

假设所求多项式系数序列为$k_0,k_1,...k_{n-1}$

现在对于新的多项式a（新得到的序列，不是原来的a序列）来求卷积$$c_h=\sum_{i=0}^{n-1}a_i(w_n^{-h})^i$$

相当于对a序列又进行FFT变换，只不过，我们现在以新序列a为系数的多项式在$x=w_n^{-i}$的一系列值

相当于求$C(x)=a_0+a_1x+a_2x^2+...+a_{n-1}x^{n-1}$在$x=w_n^0,w_n^-1,w_n^{-2},...w_n^{-(n-1)}$的点值表示法

而我们知道$a_x=k_0+k_1w_n^x+k_2(w_n^k)^2+...=\sum_{j=0}^{n-1}k_j(w_n^x)^j$

$$\sum_{i=0}^{n-1}a_i(w_n^{-h})^i$$

$$=\sum_{i=0}^{n-1}(\sum_{j=0}^{n-1}k_j*(w_n^i)^j)(w_n^{-h})^i$$

$$=\sum_{j=0}^{n-1}k_j(\sum_{i=0}^{n-1}(w_n^{j-h})^i)$$

$$=\sum_{j=0}^{n-1}k_j(\sum_{i=0}^{n-1}w_n^{(j-h)*i})$$

由于当且只当$j=h$时，$(j-h)$才为i的倍数，其余时候为0，根据n次单位根更加复杂的性质可得（不知道的看看n次单位根预备性质）

$$\sum_{j=0}^{n-1}k_j(\sum_{i=0}^{n-1}w_n^{(j-h)*i})$$

$$=n*k_h$$

所以

$$k_h=\frac {\sum_{i=0}^{n-1}a_i(w_n^{-h})^i}{h}=\frac {c_h}{n}$$

说明：$w_n^{-i}$与$w_n^i$实部相同，虚部相反。现在知道代码中inv的作用了吧

当inv=1，表示FFT变换；当inv=-1，表示FFT逆变换

FFT(a,lim,);
FFT(b,lim,);
for(int i=;i<lim;i++)    a[i]=a[i]*b[i];
FFT(a,lim,-1);
//经过FFT逆变换之后，a序列虚部都已经为0，只有实部有值，且为整数
for(int i=;i<n+m-;i++)    printf("%d ",(int)(a[i].real()/lim+0.5));//实部根据前面推导要除以n（这里除以lim）

为啥要加0.5捏：首先我们确定答案肯定是整数，但是在代码实现过程中，由于有$\pi$介入计算，导致答案可能变小了（误差很小），所以加一个0.5，然后强制类型转换切掉小数部位

比如说本来答案是1，但是代码实现的结果可能是0.999999999999，此时加上了0.5，然后转换为int，答案就是1了。

强调一遍$$w_n^k=cos\frac{2k\pi}{n}+i\,sin\frac{2k\pi}{n}$$

FFT代码

#include <complex>//c++自带复数模板
typedef complex<double> Complex;//重定义数据类型，记得要用double类型
void FFT(Complex *a,int n,int inv){
//a是你要进行变换的数组（多项式系数数组），n是数组大小，inv=1表示正变换，inv=-1表示逆变换
    if(n==)    return;//如果分治后的序列大小为1，就直接返回，不用继续分治了
    int mid=n>>;//如果n不等于1，那就继续分治，mid是分治后变成两个序列的长度
    static Complex b[];//创建一个辅助用的b数组，后面体现用处
    for(int i=;i<mid;i++)    b[i]=a[*i],b[i+mid]=a[*i+];//将a数组奇数位置的值和偶数位置的值分开，b数组前mid个位置存a数组偶数位置值，后mid个位置存a数组奇数位置值
    for(int i=;i<n;i++)    a[i]=b[i];//将b数组值重新赋给a数组 

    //对分治后的两个序列（一个是a数组前mid个元素组成的序列，另一个数a数组后mid元素组成的序列） 进行FFT变换
    FFT(a,mid,inv);
    FFT(a+mid,mid,inv);

    //算出一半，得到另一半的值，a数组前mid元素相当于之前说的f1，a数组后mid元素相当于之前说的f2
    for(int i=;i<mid;i++){
        Complex com(cos(*pi*i/n),inv*sin(*pi*i/n));
        b[i]=a[i]+com*a[i+mid];b[i+mid]=a[i]-com*a[i+mid];
    }

    for(int i=;i<n;i++)    a[i]=b[i];//重新将b数组赋值给a数组
    return;
}

FFT变换

---

FFT系数储存注意

---

在进行FFT之前，我们有两个多项式系数序列，用数组存系数的不要用普通的数组存，而要用复数数组，因为在计算的时候系数涉及复数计算，所以这样

#include <complex>//c++自带复数模板
Complex a[],b[];

for(int i=;i<n;i++)    scanf("%d",&t),a[i]=Complex(t,);//构造函数
for(int i=;i<m;i++)    scanf("%d",&t),b[i]=Complex(t,);

这样，复数的实部存系数的值，虚部为0

一个算多项式相乘后系数序列的程序

//开头说明一下，最下面有输入输出样例 

#include <iostream>

#include <cmath>
#define pi acos(-1)

#include <complex>//c++自带复数模板
using namespace std;
typedef complex<double> Complex;//重定义数据类型，记得要用double类型 

Complex a[],b[];
int n,m;

void FFT(Complex *a,int n,int inv){
//a是你要进行变换的数组（多项式系数数组），n是数组大小，inv=1表示正变换，inv=-1表示逆变换
    if(n==)    return;//如果分治后的序列大小为1，就直接返回，不用继续分治了
    int mid=n>>;//如果n不等于1，那就继续分治，mid是分治后变成两个序列的长度
    static Complex b[];//创建一个辅助用的b数组，后面体现用处
    for(int i=;i<mid;i++)    b[i]=a[*i],b[i+mid]=a[*i+];//将a数组奇数位置的值和偶数位置的值分开，b数组前mid个位置存a数组偶数位置值，后mid个位置存a数组奇数位置值
    for(int i=;i<n;i++)    a[i]=b[i];//将b数组值重新赋给a数组 

    //对分治后的两个序列（一个是a数组前mid个元素组成的序列，另一个数a数组后mid元素组成的序列） 进行FFT变换
    FFT(a,mid,inv);
    FFT(a+mid,mid,inv);

    //算出一半，得到另一半的值，a数组前mid元素相当于之前说的f1，a数组后mid元素相当于之前说的f2
    for(int i=;i<mid;i++){
        Complex com(cos(*pi*i/n),inv*sin(*pi*i/n));
        b[i]=a[i]+com*a[i+mid];b[i+mid]=a[i]-com*a[i+mid];
    }

    for(int i=;i<n;i++)    a[i]=b[i];//重新将b数组赋值给a数组
    return;
}
int main(){
    cin>>n>>m;//输入两个多项式的项数
    int k=n+m,lim=,t;
    for(int i=;i<n;i++)    scanf("%d",&t),a[i]=Complex(t,);//第一个多项式系数
    for(int i=;i<m;i++)    scanf("%d",&t),b[i]=Complex(t,);//第二个多项式系数
    while(k>>=)    lim<<=;
    if(lim<n+m)    lim<<=;
    FFT(a,lim,);
    FFT(b,lim,);
    for(int i=;i<lim;i++)    a[i]=a[i]*b[i];
    FFT(a,lim,-);
    for(int i=;i<n+m-;i++)    printf("%d ",(int)(a[i].real()/lim+0.5));
}
/* 

//输入
2 3//第一个多项式有两项 ，第二个多项式有三项
1 2//第一个多项式为(1+2x)
2 1 2//第二个多项式为(2+x+2x^2) 

//输出
2 5 4 4//(1+2x)*(2+x+2x^2)=2+5x+4x^2+4x^3,系数为2 5 4 4

*/

多项式相乘

测试用例

//输入
 //两个多项式都有两项
 //第一个多项式为(1+x)
 //第二个多项式为(1+x)
//输出
  //(1+x)*(1+x)=1+2*x+x^2,系数为1 2 1 

测试

---

FFT变换的示例演示

---

在讲FFT迭代版本之前，我打算先用一个例子来展示FFT变换，加深认识

假设

　　多项式$f(x)=3+2x+x^2$

　　多项式$g(x)=2+x+2x^2$

在草稿纸上算一下，这两个多项式相乘的结果为$h(x)=6+7x+10x^2+5x^3+2x^4$

先得到$f(x)$与$g(x)$多项式的系数序列，注意应该写成复数形式的序列（复数形式为(real,image)）

　　多项式$f(x)$的系数序列为$A=\left\{(3,0),(2,0),(1,0)\right\}$

　　多项式$g(x)$的系数序列为$B=\left\{(2,0),(1,0),(2,0)\right\}$

然后判断两个多项式相乘后有多少项，应该不超过3+3=6项。而大于6的最小2次幂应该为8，所以要把两个多项式序列补成8项。

故（用(0,0)来补项）

　　多项式$f(x)$的系数序列为$A=\left\{(3,0),(2,0),(1,0),(0,0),(0,0),(0,0),(0,0),(0,0)\right\}$

　　多项式$g(x)$的系数序列为$B=\left\{(2,0),(1,0),(2,0),(0,0),(0,0),(0,0),(0,0),(0,0)\right\}$

对于每一个$f(w_8^i)$，可以寻得规律

$f(w_8^i)=A_0+A_1w_8^i+A_2(w_8^i)^2+A_3(w_8^i)^3+A_4(w_8^i)^4+A_5(w_8^i)^5+A_6(w_8^i)^6+A_7(w_8^i)^7$

$=A_0+A_2(w_8^i)^2+A_4(w_8^i)^4+A_6(w_8^i)^6+w_8^i(A_1+A_3(w_8^i)^2+A_5(w_8^i)^4+A_7(w_8^i)^6)$

$=A_0+A_2w_4^i+A_4(w_4^i)^2+A_6(w_4^i)^3+w_8^i(A_1+A_3w_4^i+A_5(w_4^i)^2+A_7(w_4^i)^3)$

$=A_0+A_4(w_4^i)^2+w_4^i(A_2+A_6(w_4^i)^2)+w_8^i(A_1+A_5(w_4^i)^2+w_4^i(A_3+A_7(w_4^i)^2))$

$=A_0+A_4w_2^i+w_4^i(A_2+A_6w_2^i)+w_8^i(A_1+A_5w_2^i+w_4^i(A_3+A_7w_2^i))$

然后

$f(w_8^{i+4})=f(-w_8^i)=A_0+A_1(-w_8^i)+A_2(-w_8^i)^2+A_3(-w_8^i)^3+A_4(-w_8^i)^4+A_5(-w_8^i)^5+A_6(-w_8^i)^6+A_7(-w_8^i)^7$

$=A_0+A_2(w_8^i)^2+A_4(w_8^i)^4+A_6(w_8^i)^6-w_8^i(A_1+A_3(w_8^i)^2+A_5(w_8^i)^4+A_7(w_8^i)^6)$

只要算出来$A_0+A_2w_4^i+A_4(w_4^i)^2+A_6(w_4^i)^3$和$A_1+A_3w_4^i+A_5(w_4^i)^2+A_7(w_4^i)^3$的值，就可以算出$f(w_8^i)$和$f(w_8^{i+4})$的值

同理，算出$A_0+A_4(w_4^i)^2$和$A_2+A_6w_2^i$的值，不仅可以得到$A_0+A_2w_4^i+A_4(w_4^i)^2+A_6(w_4^i)^3$的值，还可以得到$A_0+A_2w_4^{i+2}+A_4(w_4^{i+2})^2+A_6(w_4^{i+2})^3$

然后将每一个序列分成长度为2的小序列(下面是用1~8来编号的)

后面的是重点，对于每一个长度为2的小序列（设为(x,y)）:

　　第一个元素$x$重新赋值为$x+w_1^0*y$

　　第二个元素$y$重新赋值为$x-w_1^0*y$

(这个$w_1^1$这样来的：$w_{当前序列一半长度l}^{一半长度l的第i个元素,i从0到l-1}$)

重新赋值完之后就可以合并了，每两个长度为2的相邻序列合并为一个长度为4的序列

对于每一个长度为4的序列（设为(a,b,c,d)）:

　　第一个元素$a$重新赋值为$a+w_2^0*c$

　　第三个元素$c$重新赋值为$a-w_2^0*c$

　　第二个元素$b$重新赋值为$b+w_2^1*d$

　　第四个元素$d$重新赋值为$b-w_2^1*d$

重新赋值完之后就可以合并了，每两个长度为4的相邻序列合并为一个长度为8的序列（此时全部小序列已经合并为一个序列了）

对于整个序列（长度为8），按照上面的赋值方法重新赋值（可以参考代码），于是FFT变换就ok了

两个序列就变成了

　　$A=\left\{A_0',A_1',A_2',A_3',A_4',A_5',A_6',A_7'\right\}$

　　$B=\left\{B_0',B_1',B_2',B_3',B_4',B_5',B_6',B_7'\right\}$

将两个序列对应元素相乘，得到新序列

　　$C=\left\{A_0'*B_0',A_1'*B_1',A_2'*B_2',A_3'*B_3',A_4'*B_4',A_5'*B_5',A_6'*B_6',A_7'*B_7'\right\}$

然后将C序列进行FFT逆变换，就是多项式相乘后的系数序列了。

ps：FFT逆变换就是把当前序列再来一次FFT变换，只不过在重新赋值环节的时候是乘上$w_{mid}^{-1}$，而不是$w_{mid}^i$，最后得到的序列虚部为0，将实部全部除以8即可（这里不懂参考代码或前面逆变换的讲解）

---

FFT迭代版本

---

FFT的序列更新规律

综上所述，FFT的序列更新是有规律的，先把序列分解为序列长度为2的小段，每一段更新完毕后就合并小段，继续一组一组更新，再合并，最后合并成一个序列，然后再最后一次更新完毕。

如图所示：

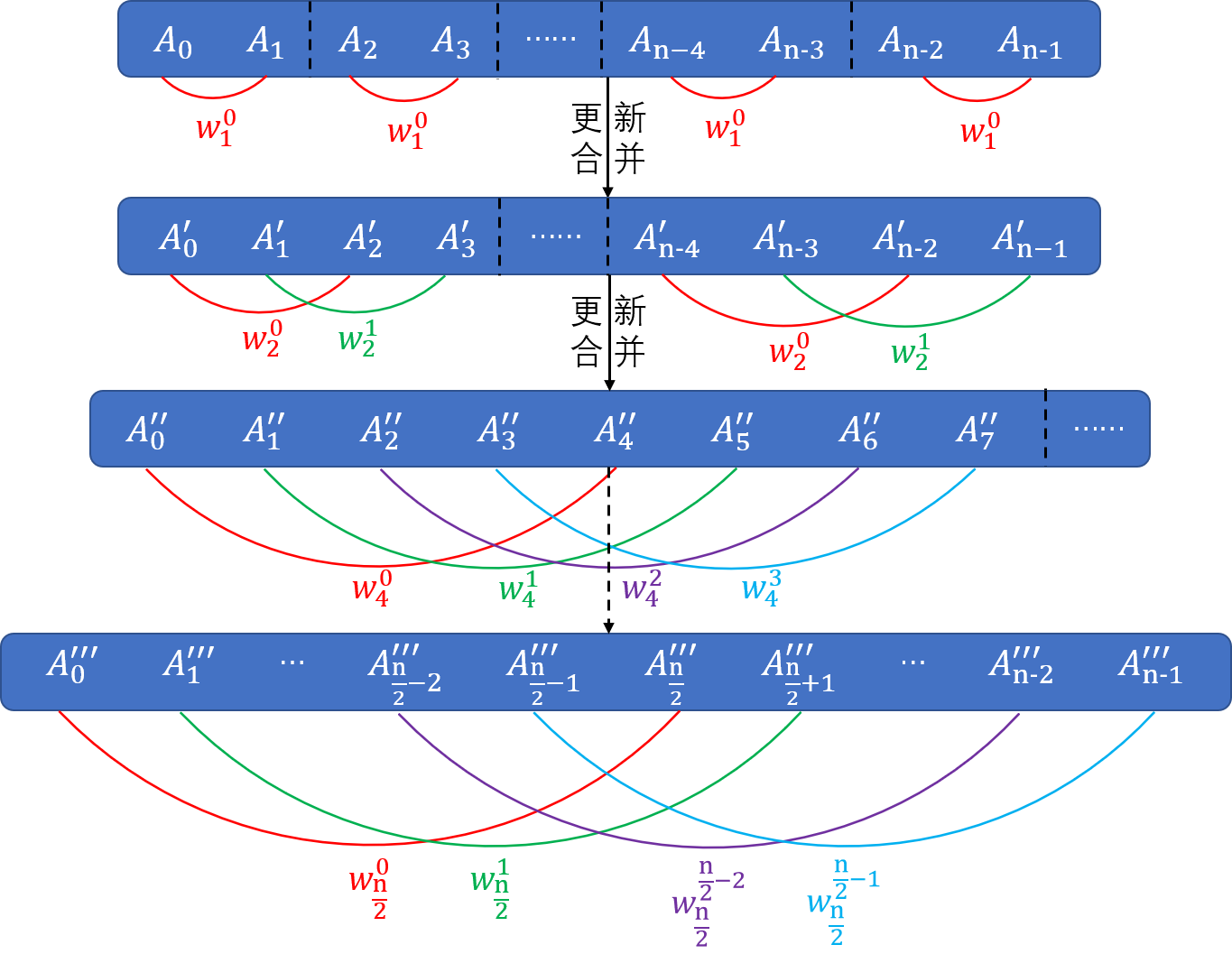
最后序列$\left\{A_0''',A_1''',...,A_{n-1}'''\right\}$为原序列进过FFT变换后的序列。

不像递归版本，迭代版本是直接从每一个小区间开始更新，然后合并，然后更新...，但是我们需要找到原系数序列经过奇偶分离的一系列操作后每个值的位置发生了什么变化。

假设原系数序列为$\left\{A_0,A_1,A_2,A_3,A_4,A_5,A_6,A_7\right\}$，下图是奇偶分离的示意图

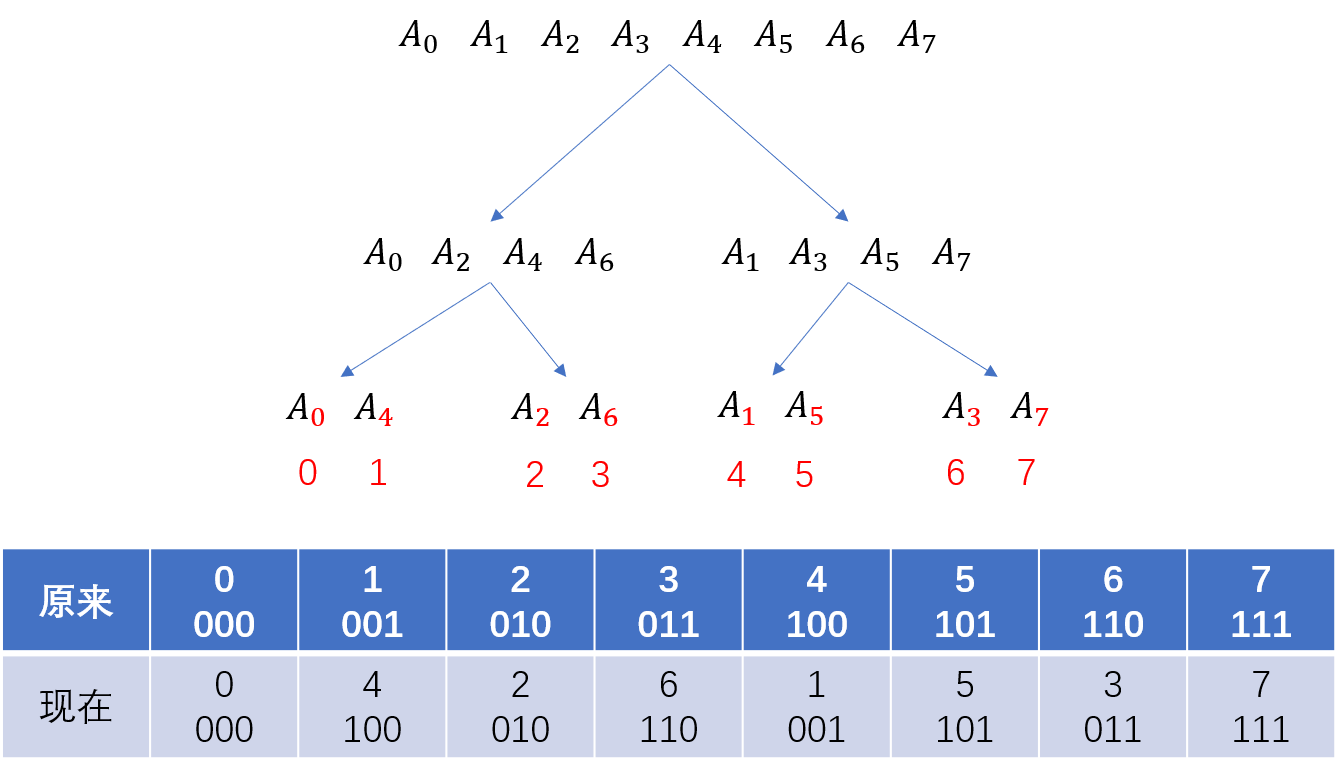
没错，这不是巧合，序列经过奇偶分离之后，前后位置数的二进制是对称的，根据这一点我们就不需要用递归来实现，可以直接来得到奇偶分离最终序列，然后再进行FFT

FFT代码

FFT迭代版比递归版快的不是一点。。

关于序列奇偶分离可以用下面方法

int rev[(n+2)>>1];
for(i=;i<n;i++){
        rev[i]=(rev[i>>]>>)|((i&)<<(bit-));
        if (i<rev[i])swap(a[i],a[rev[i]]);
}

于是就可以实现迭代版本FFT

void FFT(Complex *a,int n,int inv){
    int bit=,i,rev[(n+)>>];
    while((<<bit)<n)    bit++;
    //交换序列
    for(i=;i<n;i++){
        rev[i]=(rev[i>>]>>)|((i&)<<(bit-));
        if (i<rev[i])swap(a[i],a[rev[i]]);//if来保证只存在小的和大的交换，不会发生大的和小的交换
    }
    for (int mid=;mid<n;mid*=){//mid枚举区间长度的一半
        Complex com(cos(pi/mid),inv*sin(pi/mid));//单位根
        for (int i=;i<n;i+=mid*){//i来枚举每个区间的开头位置
            Complex omega(,);
            for (int j=;j<mid;j++,omega*=com){//j枚举每个区间的前一半元素
                Complex x=a[i+j],y=omega*a[i+j+mid];
                a[i+j]=x+y,a[i+j+mid]=x-y;//蝴蝶效应
            }
        }
    }
}

FFT变换（迭代版）

---

总接代码

---

FFT递归版本

void FFT(Complex *a,int n,int inv){
//a是你要进行变换的数组（多项式系数数组），n是数组大小，inv=1表示正变换，inv=-1表示逆变换
    if(n==)    return;//如果分治后的序列大小为1，就直接返回，不用继续分治了
    int mid=n>>;//如果n不等于1，那就继续分治，mid是分治后变成两个序列的长度
    static Complex b[];//创建一个辅助用的b数组，后面体现用处
    for(int i=;i<mid;i++)    b[i]=a[*i],b[i+mid]=a[*i+];//将a数组奇数位置的值和偶数位置的值分开，b数组前mid个位置存a数组偶数位置值，后mid个位置存a数组奇数位置值
    for(int i=;i<n;i++)    a[i]=b[i];//将b数组值重新赋给a数组 

    //对分治后的两个序列（一个是a数组前mid个元素组成的序列，另一个数a数组后mid元素组成的序列） 进行FFT变换
    FFT(a,mid,inv);
    FFT(a+mid,mid,inv);

    //算出一半，得到另一半的值，a数组前mid元素相当于之前说的f1，a数组后mid元素相当于之前说的f2
    for(int i=;i<mid;i++){
        Complex com(cos(*pi*i/n),inv*sin(*pi*i/n));//
        b[i]=a[i]+com*a[i+mid];b[i+mid]=a[i]-com*a[i+mid];
//        cout<<n<<" "<<i<<" "<<b[i].real()<<" "<<b[i].imag()<<endl;
    }

    for(int i=;i<n;i++)    a[i]=b[i];//重新将b数组赋值给a数组
    return;
}

FFT变换（迭代版）

FFT迭代版本

void FFT(Complex *a,int n,int inv){
//a是你要进行变换的数组（多项式系数数组），n是数组大小，inv=1表示正变换，inv=-1表示逆变换
    int bit=,i,rev[(n+)>>];
    while((<<bit)<n)    bit++;
    //交换序列
    for(i=;i<n;i++){
        rev[i]=(rev[i>>]>>)|((i&)<<(bit-));
        if (i<rev[i])swap(a[i],a[rev[i]]);//if来保证只存在小的和大的交换，不会发生大的和小的交换
    }
    for (int mid=;mid<n;mid*=){//mid枚举区间长度的一半
        Complex com(cos(pi/mid),inv*sin(pi/mid));//单位根
        for (int i=;i<n;i+=mid*){//i来枚举每个区间的开头位置
            Complex omega(,);
            for (int j=;j<mid;j++,omega*=com){//j枚举每个区间的前一半元素
                Complex x=a[i+j],y=omega*a[i+j+mid];
                a[i+j]=x+y,a[i+j+mid]=x-y;//蝴蝶效应
            }
        }
    }
}

FFT变换（迭代版）

---