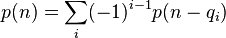hdu 4651 Partition(整数拆分+五边形数)
Partition
Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 462 Accepted Submission(s): 262
Now, I will give you a number n, and please tell me P(n) mod 1000000007.
5
11
15
19
56
176
490
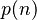 的生成函数是
的生成函数是
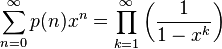 (1)
(1)- 再
利用五边形数定理可得到以下的展开式:
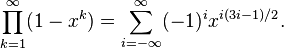 (2)
(2)- 将(2)式带入(1)式,并乘到(1)式的左边,进行展开,合并同类项,根据非常数项的系数为0!!
- 即将
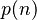 生成函数配合五边形数定理,可以得到以下的递归关系式
生成函数配合五边形数定理,可以得到以下的递归关系式
#include<stdio.h>
typedef long long ll;
const int mo=;
ll p[];
void pre()//打表,欧拉函数的倒数是分割函数的母函数!!!
{
p[]=;
for(ll i=;i<=;i++)
{
ll t=,ans=,kk=;
while()
{
ll tmp1,tmp2;
tmp1=(*kk*kk-kk)/;
tmp2=(*kk*kk+kk)/;
if(tmp1>i)break;
ans=(ans+t*p[i-tmp1]+mo)%mo;
if(tmp2>i)break;
ans=(ans+t*p[i-tmp2]+mo)%mo;
t=-t;
kk++;
}
p[i]=ans;
}
}
int main()
{
pre();
int T,n;
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
printf("%lld\n",p[n]);
}
}
hdu 4651 Partition(整数拆分+五边形数)的更多相关文章
- HDU 4651 Partition 整数划分,可重复情况
Partition Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total S ...
- HDU 4651 Partition(整数拆分)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=4651 题意:给出n.求其整数拆分的方案数. i64 f[N]; void init(){ f[0 ...
- hdu 4651 Partition (利用五边形定理求解切割数)
下面内容摘自维基百科: 五边形数定理[编辑] 五边形数定理是一个由欧拉发现的数学定理,描写叙述欧拉函数展开式的特性[1] [2].欧拉函数的展开式例如以下: 亦即 欧拉函数展开后,有些次方项被消去,仅 ...
- hdu - 4651 - Partition
题意:把一个整数N(1 <= N <= 100000)拆分不超过N的正整数相加,有多少种拆法. 题目链接:http://acm.hdu.edu.cn/showproblem.php?pid ...
- HDU-4651 Partition 整数拆分,递推
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=4651 题意:求n的整数拆为Σ i 的个数. 一般的递归做法,或者生成函数做法肯定会超时的... 然后要 ...
- hdu 4651 Partition && hdu 4658 Integer Partition——拆分数与五边形定理
题目:http://acm.hdu.edu.cn/showproblem.php?pid=4651 参考:https://blog.csdn.net/u013007900/article/detail ...
- hdu 4651 - Partition(五边形数定理)
定理详见维基百科....http://zh.wikipedia.org/wiki/%E4%BA%94%E9%82%8A%E5%BD%A2%E6%95%B8%E5%AE%9A%E7%90%86 代码如下 ...
- HDU 4651 (生成函数)
HDU 4651 Partition Problem : n的整数划分方案数.(n <= 100008) Solution : 参考资料: 五角数 欧拉函数 五边形数定理 整数划分 一份详细的题 ...
- 【hdu 4658】Integer Partition (无序分拆数、五边形数定理)
hdu 4658 Integer Partition 题意 n分拆成若干个正整数的和,每个正整数出现小于k次,分拆方案有多少.(t<=100,n<=1e5) 题解 之前写过一篇Partit ...
随机推荐
- 运行PHP出现No input file specified错误解决办法
配置了一台新服务器,使用的是IIS + Fastcgi + PHP 5.3.X,访问php页面的时候就会报错“No input file specified” 在php.ini文件里面修改: 1.增加 ...
- JSP XML数据处理
JSP XML数据处理 当通过HTTP发送XML数据时,就有必要使用JSP来处理传入和流出的XML文档了,比如RSS文档.作为一个XML文档,它仅仅只是一堆文本而已,使用JSP创建XML文档并不比创建 ...
- elasticsearch堆内存的配置建议
1.将最小堆大小(Xms)和最大堆大小(Xmx)设置为彼此相等 防止内存抖动 2:给多大的堆内存? 给ES的内存配置不是越大越好,建议不能超过32GB,不同jdk版本最大边界值是不同的,对于32位小于 ...
- MySQL高可用架构之MySQL5.7.19 PXC
CentOS7.3下Percona-XtraDB-Cluster-5.7.19集群部署PXC三节点安装:node1:10.10.10.11 node2:10.10.10.12node3:10.10.1 ...
- Mysql数据库密码忘记的解决办法
密码忘记——破解密码 跳过授权方式,直接登录!! 1.以管理员身份打开cmd 2.停掉mysql服务端 C:\WINDOWS\system32>net stop mysql MySQL 服务正在 ...
- Jeecg心得篇--这个世界不缺程序员,而是缺少匠人和架构师
真正的快乐,是用自己喜欢的方式过完这一生.来人间一趟,不能只为了活着. 这个世界不缺程序员,而是缺少匠人精神的架构师与产品经理. 因为他们通过自己的行为与理念默默地改变着世界,一个更好的世界. 这是我 ...
- fedora23安装php,mysql
httpd: 他的服务器根: ServerRoot, 是在/etc/httpd. 因为httpd所有的配置文件, 运行文件等都在这里.所以这是他的根. httpd的配置文件: httpd.conf恰好 ...
- 纯CSS3写一个立方体并在鼠标悬停的时候无限循环旋转
- Linux_FTP服务器
目录 目录 FTP FTP Server FTP configuration Global config Anonymous user FTP Config Virtual user FTP Loca ...
- 阶段1 语言基础+高级_1-3-Java语言高级_1-常用API_1_第4节 ArrayList集合_16-ArrayList练习一_存储随机数
循环6次就是6.fori 循环子在外部+1就是得到的1到33的数字 list.fori遍历集合 自动生for循环的代码