6353. 【NOIP2019模拟】给(ca)

题目描述

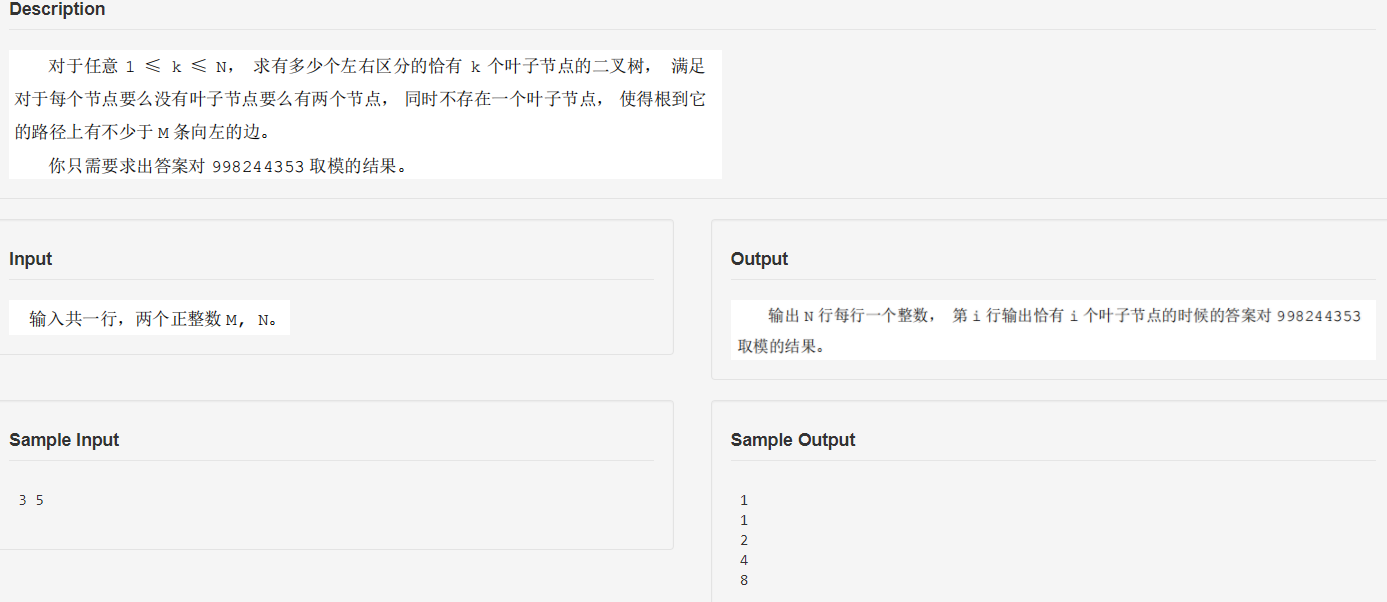
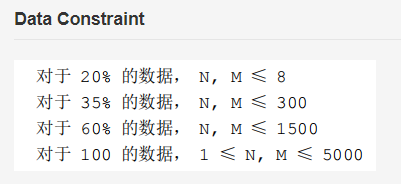
题解

虫合

由于前几天被教♂育了，所以大力找了一发规律

先把m-1，设f[i][j]表示m≤i，有j个叶子节点的答案

转移显然，也显然是O(n^3)的

---

把f打出来后长这样：

1 1 1 1 1 1 1 1 1 1 1 1 1 1 1

1 1 2 4 8 16 32 64 128 256 512 1024 2048 4096 8192

1 1 2 5 13 34 89 233 610 1597 4181 10946 28657 75025 196418

1 1 2 5 14 41 122 365 1094 3281 9842 29525 88574 265721 797162

1 1 2 5 14 42 131 417 1341 4334 14041 45542 147798 479779 1557649

1 1 2 5 14 42 132 428 1416 4744 16016 54320 184736 629280 2145600

1 1 2 5 14 42 132 429 1429 4846 16645 57686 201158 704420 2473785

1 1 2 5 14 42 132 429 1430 4861 16778 58598 206516 732825 2613834

1 1 2 5 14 42 132 429 1430 4862 16795 58766 207783 740924 2660139

1 1 2 5 14 42 132 429 1430 4862 16796 58785 207990 742626 2671892

1 1 2 5 14 42 132 429 1430 4862 16796 58786 208011 742876 2674117

1 1 2 5 14 42 132 429 1430 4862 16796 58786 208012 742899 2674414

1 1 2 5 14 42 132 429 1430 4862 16796 58786 208012 742900 2674439

1 1 2 5 14 42 132 429 1430 4862 16796 58786 208012 742900 2674440

1 1 2 5 14 42 132 429 1430 4862 16796 58786 208012 742900 2674440

显然第i行的前i+1个是正常的卡特兰数，从i+2项开始就不同了

可以发现：

\(f[1][i]=f[1][i-1]*1\)

\(f[2][i]=f[2][i-1]*2\)

\(f[3][i]=f[3][i-1]*3-f[3][i-2]*1\)

\(f[4][i]=f[4][i-1]*4-f[4][i-2]*6\)

\(f[5][i]=f[5][i-1]*5-f[5][i-2]*10+f[5][i-3]*1\)

猜想：

\(f[i][j]=\sum{f[i][j-k]*a[i][k]}\)

通过暴力枚举后可以把前几项的a搞出来：

1：1

2：2

3：3 -1

4：4 -3

5：5 -6 1

6：6 -10 4

7：7 -15 10 -1

8：8 -21 20 -5

钦定\(a[1...m][0]=1,a[1][1]=1,a[2][1]=2\)之后，可以发现一个神奇的式子：

\(a[i][j]=a[i-1][j]+a[i-2][j-1]\)

于是可以推出\(a[m]\)，再推出\(f[m]\)即可

code

#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define mod 998244353
using namespace std;

long long a[5001][5001];
long long f[5001];
int n,m,i,j,k,l;

int main()
{
	freopen("ca.in","r",stdin);
	freopen("ca.out","w",stdout);
//	freopen("a.out","w",stdout);

	fo(i,1,5000)
	a[i][0]=1;
	a[1][1]=1;
	a[2][1]=2;
	fo(i,3,5000)
	{
		fo(j,1,5000)
		a[i][j]=(a[i-1][j]+a[i-2][j-1])%mod;
	}

	scanf("%d%d",&m,&n);
	--m;
	f[1]=1;
	fo(i,2,m+1)
	{
		fo(j,1,i-1)
		f[i]=(f[i]+f[j]*f[i-j]%mod)%mod;
	}

	fo(i,m+2,n)
	{
		k=1;
		fd(j,i-1,1)
		{
			f[i]=(f[i]+f[j]*a[m][i-j]*k%mod)%mod;
			k=-k;
		}
	}

	fo(i,1,n)
	printf("%lld\n",(f[i]+mod)%mod);

	fclose(stdin);
	fclose(stdout);

	return 0;
}

官方题解

其实也不难，设\(f[i][j]\)表示放了i个点，从根到当前点需要向左走j步

那么\(f[i][j]\)可以走到自己的左儿子，或是走到最后一个向左走的那个点的右儿子，即\(f[i][j]-->f[i+1][j+1],f[i+1][j-1]\)

这样转移的本质是按dfs序走，最后的答案为\(f[2k-1][0]\)（最后一个点必定只能向右走）

code

#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define mod 998244353
#define min(a,b) (a<b?a:b)
using namespace std;

int f[10001][5002];
int n,m,i,j,k,l;

int main()
{
	freopen("ca.in","r",stdin);
	freopen("ca.out","w",stdout);

	scanf("%d%d",&m,&n);--m;
	f[1][0]=1;

	fo(i,1,n+n-2)
	{
		fd(j,min(m,i-1),0)
		if (f[i][j])
		{
			f[i+1][j+1]=(f[i+1][j+1]+f[i][j])%mod;
			if (j>0)
			f[i+1][j-1]=(f[i+1][j-1]+f[i][j])%mod;
		}
	}

	for (i=1; i<=n+n-1; i+=2)
	printf("%d\n",f[i][0]);

	fclose(stdin);
	fclose(stdout);

	return 0;
}