[洛谷P2296] NOIP2014 寻找道路

问题描述

在有向图G 中，每条边的长度均为1 ，现给定起点和终点，请你在图中找一条从起点到终点的路径，该路径满足以下条件：

1 ．路径上的所有点的出边所指向的点都直接或间接与终点连通。

2 ．在满足条件1 的情况下使路径最短。

注意：图G 中可能存在重边和自环，题目保证终点没有出边。

请你输出符合条件的路径的长度。

输入格式

第一行有两个用一个空格隔开的整数n 和m ，表示图有n 个点和m 条边。

接下来的m 行每行2 个整数x 、y ，之间用一个空格隔开，表示有一条边从点x 指向点y 。

最后一行有两个用一个空格隔开的整数s 、t ，表示起点为s ，终点为t 。

输出格式

输出只有一行，包含一个整数，表示满足题目描述的最短路径的长度。如果这样的路径不存在，输出- 1 。

样例输入输出

样例输入1

3 2

1 2

2 1

1 3

样例输出1

-1

样例输入2

6 6

1 2

1 3

2 6

2 5

4 5

3 4

1 5

样例输出2

3

说明

解释1：

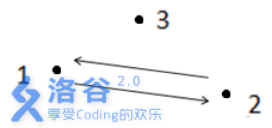
如上图所示，箭头表示有向道路，圆点表示城市。起点1 与终点3 不连通，所以满足题

目᧿述的路径不存在，故输出- 1 。

解释2：

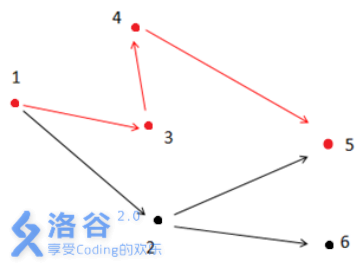
如上图所示，满足条件的路径为1 - >3- >4- >5。注意点2 不能在答案路径中，因为点2连了一条边到点6 ，而点6 不与终点5 连通。

对于30%的数据，0<n≤10，0<m≤20；

对于60%的数据，0<n≤100，0<m≤2000；

对于100%的数据，0<n≤10,000，0<m≤200,000，0<x，y，s，t≤n，x≠t。

解析

• 首先建反图，找到能够到达终点的点。
• 然后在原图上确认哪些点是不满足条件的。
• 然后BFS，不经过不满足条件的点，得到答案。

代码

#include <iostream>
#include <cstdio>
#include <queue>
#include <cstring>
#define N 10002
#define M 200002
using namespace std;
struct edge{
    int u,v;
}e[M];
struct node{
    int x,d;
    node(int _x,int _d){
        x=_x,d=_d;
    }
};
int head[N],ver[M],nxt[M],l;
int n,m,s,t,i,j;
bool f[N],vis[N];
int read()
{
    char c=getchar();
    int w=0;
    while(c<'0'||c>'9') c=getchar();
    while(c<='9'&&c>='0'){
        w=w*10+c-'0';
        c=getchar();
    }
    return w;
}
void insert(int x,int y)
{
    l++;
    ver[l]=y;
    nxt[l]=head[x];
    head[x]=l;
}
void bfs1()
{
    queue<int> q;
    q.push(t);
    f[t]=1;
    while(!q.empty()){
        int x=q.front();
        q.pop();
        for(int i=head[x];i;i=nxt[i]){
            int y=ver[i];
            if(!f[y]){
                f[y]=1;
                q.push(y);
            }
        }
    }
}
int bfs2()
{
    queue<node> q;
    q.push(node(s,0));
    memset(f,0,sizeof(f));
    f[s]=1;
    while(!q.empty()){
        int x=q.front().x,d=q.front().d;
        q.pop();
        for(int i=head[x];i;i=nxt[i]){
            int y=ver[i];
            if(!f[y]&&vis[y]){
                f[y]=1;
                if(y==t) return d+1;
                q.push(node(y,d+1));
            }
        }
    }
    return -1;
}
int main()
{
    n=read();m=read();
    for(i=1;i<=m;i++){
        e[i].u=read(),e[i].v=read();
        insert(e[i].v,e[i].u);
    }
    s=read();t=read();
    bfs1();
    memset(head,0,sizeof(head));
    memset(vis,1,sizeof(vis));
    l=0;
    for(i=1;i<=m;i++) insert(e[i].u,e[i].v);
    for(i=1;i<=n;i++){
        for(j=head[i];j;j=nxt[j]){
            if(!f[ver[j]]) vis[i]=0;
        }
    }
    cout<<bfs2()<<endl;
    return 0;
}