KD-Tree 学习笔记
这是一篇又长又烂的学习笔记，请做好及时退出的准备。
KD-Tree 的复杂度大概是 \(O(n^{1-\frac{1}{k}})\)
\(k\) 是维度
由于网上找不到靠谱的证明，咕了。
会证明之后再补上。
前置？
- 考虑到平衡树不能做多维，kdt就是扩展到多维情况
- 每次 \(nth\_element\) 的复杂度是 \(O(n)\) 的。
- 类似替罪羊的想法，如果树不够平衡，直接 pia 重构
- 考虑你删除元素不方便，据说只能打上标记啥的）
- 但是你插入元素不改变树的大致结构 qwqwq
建树显然是 \(n \log n\) 的
插入据说是 \(n \log^2 n\) 的
查询依旧是 \(n \log n\) 的 qwq
- 考虑建树
假设最开始有这么多个点
选一个中位数，把空间一分为二
左边作为左儿子，右边作为右儿子
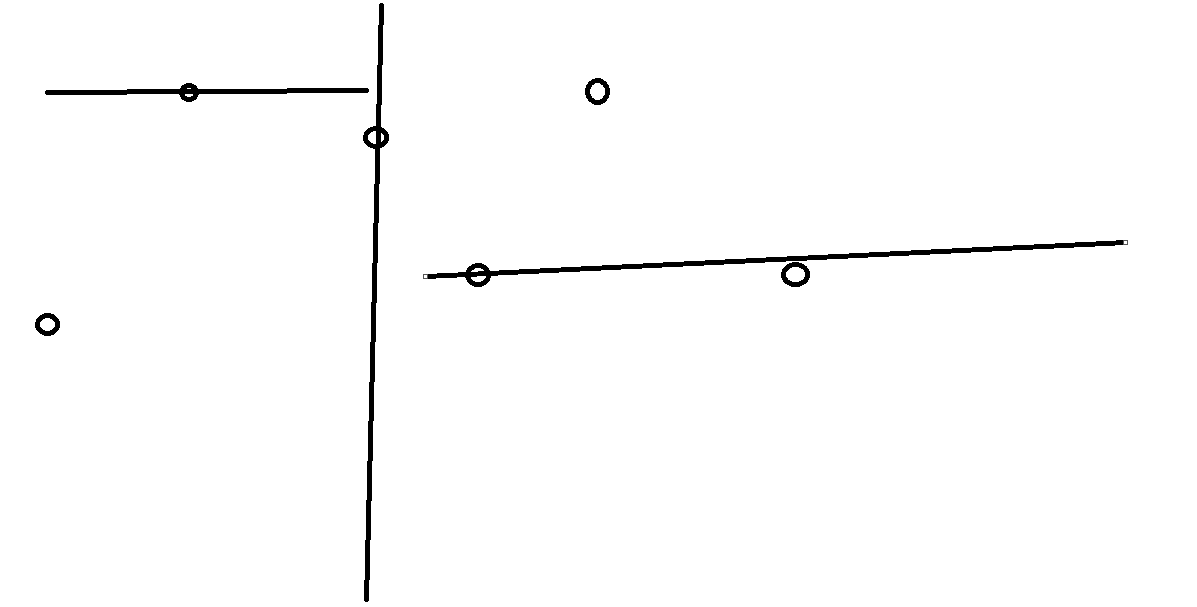
再取一次
我们定义初始是这样
类似平衡树的结构
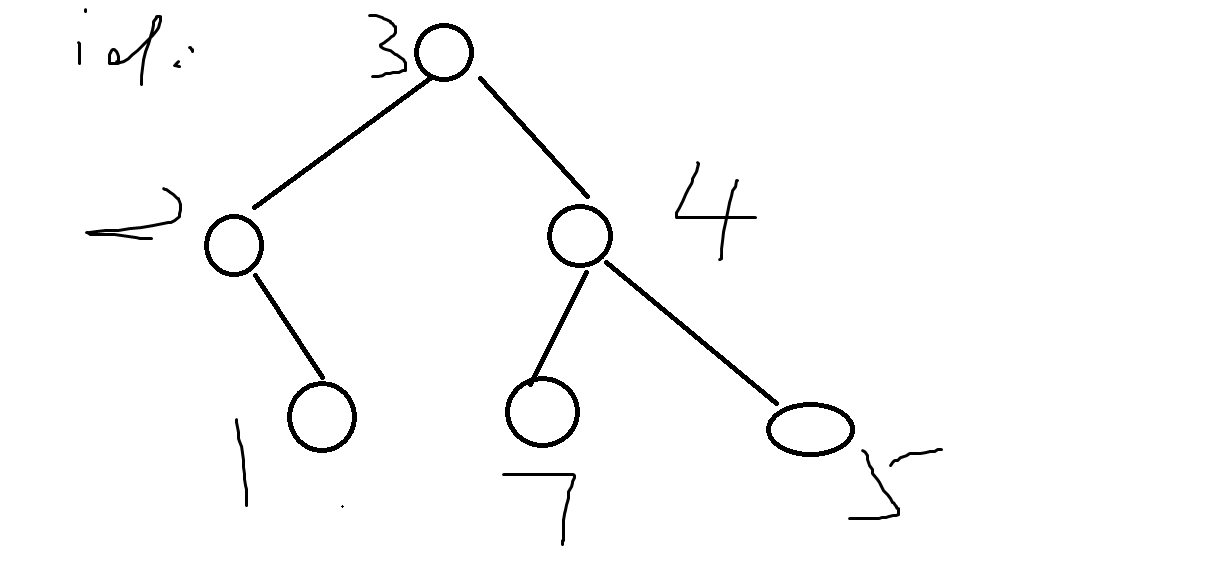
建出来的树长成这样子
然后像平衡树一样维护最小横坐标，纵坐标，最大横坐标，纵坐标，当前权值，当前坐标，sum值，就可以了。
代码亦不难
int build(int l , int r , int p) {
now = p ;
int mid = l + r >> 1 ;
nth_element(data + l , data + mid , data + r + 1) ; // data 是原数组 qwq 是 KDT
qwq[mid] = data[mid] ;
if(l < mid) qwq[mid].ls = build(l , mid - 1 , p ^ 1) ;
if(r > mid) qwq[mid].rs = build(mid + 1 , r , p ^ 1) ;
pushup(mid) ; return mid ;
}
- 考虑修改
插入时要判是否平衡，如果不平衡就擦除一整棵子树并重构。（类似替罪羊树的想法
void Erase(int x) {
if (!x) return;
pp[++m] = P[x], Erase(ls(x)), Erase(rs(x)), erase(x);
}
inline void insert(Point p) {
int top = -1, x = root;
if (!x) {
pp[1] = p, root = build(1, 1, 1);
return;
}
while (233) {
if (max(sz[ls(x)], sz[rs(x)]) > sz[x] * alpha && top == -1) top = x;
++sz[x], cmin(L[x][0], p.x), cmax(R[x][0], p.x), cmin(L[x][1], p.y), cmax(R[x][1], p.y);
int& y = ch[x][(tp[x] == 0) ? (!cmpx(p, P[x])) : (!cmpy(p, P[x]))];
if (!y) {
y = NewNode();
L[y][0] = R[y][0] = p.x, L[y][1] = R[y][1] = p.y, sz[y] = 1, tp[y] = tp[x] ^ 1, fa[y] = x, P[y] = p;
break;
}
x = y;
}
if (top == -1) return;
m = 0;
if (top == root) {
Erase(top), root = build(1, m, 1);
return;
}
int f = fa[top], &t = ch[f][(tp[f] == 0) ? (!cmpx(P[top], P[f])) : (!cmpy(P[top], P[f]))];
Erase(top), t = build(1, m, tp[f]);
}
这样就可以了
询问其实因题目而定的。。没什么具体做法
int query(int x, int l0, int r0, int l1, int r1) {
if (!x) return 0;
if (l0 <= L[x][0] && R[x][0] <= r0 && l1 <= L[x][1] && R[x][1] <= r1) return sz[x];
if (r0 < L[x][0] || R[x][0] < l0 || r1 < L[x][1] || R[x][1] < l1) return 0;
return query(ls(x), l0, r0, l1, r1) + query(rs(x), l0, r0, l1, r1) +
(l0 <= P[x].x && P[x].x <= r0 && l1 <= P[x].y && P[x].y <= r1);
}
比如这个就是二维数点查询个数的方法
然后考虑一个东西，即维数问题
像 \(cdq\)分治，你可以直接三维 \(kdt\) 直接狂 T 不止
也可以排个序然后卡卡常数过去啥的）
#include <bits/stdc++.h>
#define rep(i, x, y) for (register int i = x; i <= y; i++)
using namespace std;
using ll = long long;
using pii = pair<int, int>;
const static int _ = 1 << 20;
char fin[_], *p1 = fin, *p2 = fin;
inline char gc() { return (p1 == p2) && (p2 = (p1 = fin) + fread(fin, 1, _, stdin), p1 == p2) ? EOF : *p1++; }
inline int read() {
bool sign = 1;
char c = 0;
while (c < 48) ((c = gc()) == 45) && (sign = 0);
int x = (c & 15);
while ((c = gc()) > 47) x = (x << 1) + (x << 3) + (c & 15);
return sign ? x : -x;
}
template <class T>
void print(T x, char c = '\n') {
(x == 0) && (putchar(48)), (x < 0) && (putchar(45), x = -x);
static char _st[100];
int _stp = 0;
while (x) _st[++_stp] = x % 10 ^ 48, x /= 10;
while (_stp) putchar(_st[_stp--]);
putchar(c);
}
template <class T>
void cmax(T& x, T y) {
(x < y) && (x = y);
}
template <class T>
void cmin(T& x, T y) {
(x > y) && (x = y);
}
const double alpha = 0.7;
const int N = 1e5 + 10;
int n, k;
int ch[N][2], fa[N], sz[N], tp[N];
int L[N][2], R[N][2];
int st[N], top = 0;
#define ls(x) ch[x][0]
#define rs(x) ch[x][1]
struct Point {
int x, y, z, id;
bool operator==(const Point& other) const { return x == other.x && y == other.y && z == other.z; }
} p[N], P[N], pp[N];
inline bool cmpx(const Point& x, const Point& y) {
return (x.x == y.x) ? (x.y == y.y ? x.id < y.id : x.y < y.y) : x.x < y.x;
}
inline bool cmpy(const Point& x, const Point& y) {
return (x.y == y.y) ? (x.x == y.x ? x.id < y.id : x.x < y.x) : x.y < y.y;
}
int root = 0, cnt = 0;
inline void erase(int x) {
st[++top] = x, ls(x) = rs(x) = sz[x] = L[x][0] = R[x][0] = L[x][1] = R[x][1] = 0;
P[x] = { 0, 0, 0, 0 };
}
int m;
inline int NewNode() { return top ? st[top--] : ++cnt; }
int build(int l, int r, int lst) {
if (l > r) return 0;
int x = NewNode(), mn = 1e9, mx = -1e9;
rep(i, l, r) cmin(mn, pp[i].x), cmax(mx, pp[i].x);
L[x][0] = mn, R[x][0] = mx;
mn = 1e9, mx = -1e9;
rep(i, l, r) cmin(mn, pp[i].y), cmax(mx, pp[i].y);
L[x][1] = mn, R[x][1] = mx, tp[x] = lst ^ 1;
int mid = l + r >> 1;
(lst) ? nth_element(pp + l, pp + mid, pp + r + 1, cmpx) : nth_element(pp + l, pp + mid, pp + r + 1, cmpy);
P[x] = pp[mid], ls(x) = build(l, mid - 1, lst ^ 1), rs(x) = build(mid + 1, r, lst ^ 1);
if (ls(x)) fa[ls(x)] = x;
if (rs(x)) fa[rs(x)] = x;
sz[x] = sz[ls(x)] + sz[rs(x)] + 1;
return x;
}
void Erase(int x) {
if (!x) return;
pp[++m] = P[x], Erase(ls(x)), Erase(rs(x)), erase(x);
}
inline void insert(Point p) {
int top = -1, x = root;
if (!x) {
pp[1] = p, root = build(1, 1, 1);
return;
}
while (233) {
if (max(sz[ls(x)], sz[rs(x)]) > sz[x] * alpha && top == -1) top = x;
++sz[x], cmin(L[x][0], p.x), cmax(R[x][0], p.x), cmin(L[x][1], p.y), cmax(R[x][1], p.y);
int& y = ch[x][(tp[x] == 0) ? (!cmpx(p, P[x])) : (!cmpy(p, P[x]))];
if (!y) {
y = NewNode();
L[y][0] = R[y][0] = p.x, L[y][1] = R[y][1] = p.y, sz[y] = 1, tp[y] = tp[x] ^ 1, fa[y] = x, P[y] = p;
break;
}
x = y;
}
if (top == -1) return;
m = 0;
if (top == root) {
Erase(top), root = build(1, m, 1);
return;
}
int f = fa[top], &t = ch[f][(tp[f] == 0) ? (!cmpx(P[top], P[f])) : (!cmpy(P[top], P[f]))];
Erase(top), t = build(1, m, tp[f]);
}
int query(int x, int l0, int r0, int l1, int r1) {
if (!x) return 0;
if (l0 <= L[x][0] && R[x][0] <= r0 && l1 <= L[x][1] && R[x][1] <= r1) return sz[x];
if (r0 < L[x][0] || R[x][0] < l0 || r1 < L[x][1] || R[x][1] < l1) return 0;
return query(ls(x), l0, r0, l1, r1) + query(rs(x), l0, r0, l1, r1) +
(l0 <= P[x].x && P[x].x <= r0 && l1 <= P[x].y && P[x].y <= r1);
}
int ans[N], Cnt[N];
signed main() {
#ifdef _WIN64
freopen("testdata.in", "r", stdin);
#endif
n = read(), k = read();
rep(i, 1, n) { p[i].x = read(), p[i].y = read(), p[i].z = read(), p[i].id = i; }
sort(p + 1, p + n + 1, [](const Point& x, const Point& y) { return x.z == y.z ? cmpx(x, y) : x.z < y.z; });
for (int l = 1, r; l <= n; l = r + 1) {
r = l;
while (r < n && p[r + 1] == p[r]) insert(p[r++]);
ans[r] = query(root, -1e9, p[r].x, -1e9, p[r].y), Cnt[ans[r]] += r - l + 1, insert(p[r]);
}
rep(i, 0, n - 1) print(Cnt[i]);
return 0;
}
#include <bits/stdc++.h>
#define rep(i , x , y) for(register int i = (x) , _## i = ((y) + 1) ; i < _## i ; i ++)
#define Rep(i , x , y) for(register int i = (x) , _## i = ((y) - 1) ; i > _## i ; i --)
using namespace std ;
//#define int long long
using ll = long long ;
using pii = pair < int , int > ;
const static int _ = 1 << 20 ;
char fin[_] , * p1 = fin , * p2 = fin ;
inline char gc() {
return (p1 == p2) && (p2 = (p1 = fin) + fread(fin , 1 , _ , stdin) , p1 == p2) ? EOF : * p1 ++ ;
}
inline int read() {
bool sign = 1 ;
char c = 0 ;
while(c < 48) ((c = gc()) == 45) && (sign = 0) ;
int x = (c & 15) ;
while((c = gc()) > 47) x = (x << 1) + (x << 3) + (c & 15) ;
return sign ? x : -x ;
}
template < class T > void print(T x , char c = '\n') {
(x == 0) && (putchar(48)) , (x < 0) && (putchar(45) , x = -x) ;
static char _st[100] ;
int _stp = 0 ;
while(x) _st[++ _stp] = x % 10 ^ 48 , x /= 10 ;
while(_stp) putchar(_st[_stp --]) ;
putchar(c) ;
}
template < class T > void cmax(T & x , T y) {
(x < y) && (x = y) ;
}
template < class T > void cmin(T & x , T y) {
(x > y) && (x = y) ;
}
struct KDT {
int x , y ;
};
bool cmp1(const KDT & x , const KDT & y) {
return x.x < y.x ;
}
bool cmp2(const KDT & x , const KDT & y) {
return x.y < y.y ;
}
int n , m , ans ;
const int N = 3e6 + 10 ;
KDT t[N] ;
int ls[N] , rs[N] , p[N][2] , mx[N][2] , mn[N][2] ;
void pushup(int x) {
cmax(mx[x][0] , mx[ls[x]][0]) , cmax(mx[x][0] , mx[rs[x]][0]) ;
cmax(mx[x][1] , mx[ls[x]][1]) , cmax(mx[x][1] , mx[rs[x]][1]) ;
cmin(mn[x][0] , mn[ls[x]][0]) , cmin(mn[x][0] , mn[rs[x]][0]) ;
cmin(mn[x][1] , mn[ls[x]][1]) , cmin(mn[x][1] , mn[rs[x]][1]) ;
}
int mxd = 0 , tot = 0 ;
void ins(int & now , int x , int y , int d , int dep) {
if(! now) {
now = ++ tot ;
p[now][0] = x ;
p[now][1] = y ;
mx[now][0] = mn[now][0] = x ;
mx[now][1] = mn[now][1] = y ;
mxd = dep ;
return ;
}
if(! d && x < p[now][d]) ins(ls[now] , x , y , d ^ 1 , dep + 1) ;
else if(! d) ins(rs[now] , x , y , d ^ 1 , dep + 1) ;
else if(y < p[now][d]) ins(ls[now] , x , y , d ^ 1 , dep + 1) ;
else ins(rs[now] , x , y , d ^ 1 , dep + 1) ;
pushup(now) ;
}
void qry(int & dis , int x , int y , int now) {
dis = 0 ;
if(x > mx[now][0]) dis += x - mx[now][0] ;
if(x < mn[now][0]) dis += mn[now][0] - x ;
if(y > mx[now][1]) dis += y - mx[now][1] ;
if(y < mn[now][1]) dis += mn[now][1] - y ;
}
void query(int now , int x , int y) {
int disn = abs(x - p[now][0]) + abs(y - p[now][1]) ;
cmin(ans , disn) ;
int dl = 0x3f3f3f3f ;
int dr = dl ;
if(ls[now]) qry(dl , x , y , ls[now]) ;
if(rs[now]) qry(dr , x , y , rs[now]) ;
if(dl < dr) {
if(dl < ans) query(ls[now] , x , y) ;
if(dr < ans) query(rs[now] , x , y) ;
} else {
if(dr < ans) query(rs[now] , x , y) ;
if(dl < ans) query(ls[now] , x , y) ;
}
}
int build(int l , int r , int d) {
if(l > r) return 0 ;
int mid = l + r >> 1 ;
nth_element(t + l , t + mid , t + r + 1 , d ? cmp1 : cmp2) ;
int now = ++ tot ;
mx[now][0] = mn[now][0] = p[now][0] = t[mid].x ;
mx[now][1] = mn[now][1] = p[now][1] = t[mid].y ;
ls[now] = build(l , mid - 1 , d ^ 1) ;
rs[now] = build(mid + 1 , r , d ^ 1) ;
pushup(now) ;
return now ;
}
signed main() {
#ifdef _WIN64
freopen("testdata.in" , "r" , stdin) ;
#endif
memset(mn , 0x3f , sizeof(mn)) ;
memset(mx , 0xcf , sizeof(mx)) ;
n = read() ;
m = read() ;
rep(i , 1 , n) {
t[i].x = read() ;
t[i].y = read() ;
}
build(1 , n , 0) ;
int rt = 1 ;
rep(i , 1 , m) {
int opt = read() , x = read() , y = read() ;
if(opt == 1) {
ins(rt , x , y , 0 , 1) ;
t[++ n] = { x , y } ;
if(mxd > sqrt(tot)) tot = 0 , build(1 , n , 0) ;
} else {
ans = 0x3f3f3f3f ;
query(rt , x , y) ;
print(ans) ;
}
}
return 0 ;
}
// powered by c++11
// by Isaunoya
#include<bits/stdc++.h>
#define rep(i , x , y) for(register int i = (x) ; i < (y) ; i ++)
using namespace std ;
using db = double ;
using ll = long long ;
using uint = unsigned int ;
#define int long long
using pii = pair < int , int > ;
#define ve vector
#define Tp template
#define all(v) v.begin() , v.end()
#define sz(v) ((int)v.size())
#define pb emplace_back
#define fir first
#define sec second
// the cmin && cmax
Tp < class T > void cmax(T & x , const T & y) {
if(x < y) x = y ;
}
Tp < class T > void cmin(T & x , const T & y) {
if(x > y ) x = y ;
}
// sort , unique , reverse
Tp < class T > void sort(ve < T > & v) {
sort(all(v)) ;
}
Tp < class T > void unique(ve < T > & v) {
sort(all(v)) ;
v.erase(unique(all(v)) , v.end()) ;
}
Tp < class T > void reverse(ve < T > & v) {
reverse(all(v)) ;
}
int n , m , now = 0 ;
struct node {
int d[2] , ls , rs , val , sum ;
int mx[2] , mn[2] ;
bool operator < (const node & other) const {
return d[now] < other.d[now] ;
}
} ;
const int maxn = 5e4 + 10 ;
node data[maxn] , qwq[maxn] ;
void pushup(int o) {
int ls = qwq[o].ls , rs = qwq[o].rs ;
for(int i = 0 ; i < 2 ; i ++) {
qwq[o].mx[i] = qwq[o].mn[i] = qwq[o].d[i] ;
if(ls) {
cmin(qwq[o].mn[i] , qwq[ls].mn[i]) ;
cmax(qwq[o].mx[i] , qwq[ls].mx[i]) ;
}
if(rs) {
cmin(qwq[o].mn[i] , qwq[rs].mn[i]) ;
cmax(qwq[o].mx[i] , qwq[rs].mx[i]) ;
}
}
qwq[o].sum = qwq[o].val ;
if(ls) qwq[o].sum += qwq[ls].sum ;
if(rs) qwq[o].sum += qwq[rs].sum ;
}
int build(int l , int r , int p) {
now = p ;
int mid = l + r >> 1 ;
nth_element(data + l , data + mid , data + r + 1) ;
qwq[mid] = data[mid] ;
if(l < mid) qwq[mid].ls = build(l , mid - 1 , p ^ 1) ;
if(r > mid) qwq[mid].rs = build(mid + 1 , r , p ^ 1) ;
pushup(mid) ; return mid ;
}
int a , b , c ;
int chk(int x , int y) { return x * a + y * b < c ; }
int qry(int p) {
int cnt = 0 ;
cnt += chk(qwq[p].mn[0] , qwq[p].mn[1]) ;
cnt += chk(qwq[p].mn[0] , qwq[p].mx[1]) ;
cnt += chk(qwq[p].mx[0] , qwq[p].mn[1]) ;
cnt += chk(qwq[p].mx[0] , qwq[p].mx[1]) ;
if(cnt == 4) return qwq[p].sum ;
if(! cnt) return 0 ;
int res = 0 ;
if(chk(qwq[p].d[0] , qwq[p].d[1])) res += qwq[p].val ;
if(qwq[p].ls) res += qry(qwq[p].ls) ;
if(qwq[p].rs) res += qry(qwq[p].rs) ;
return res ;
}
int rt = 0 ;
signed main() {
ios_base :: sync_with_stdio(false) ;
cin.tie(nullptr) , cout.tie(nullptr) ;
// code begin.
cin >> n >> m ;
for(int i = 1 ; i <= n ; i ++) {
cin >> data[i].d[0] >> data[i].d[1] >> data[i].val ;
}
rt = build(1 , n , 0) ;
for(int i = 1 ; i <= m ; i ++) {
cin >> a >> b >> c ;
cout << qry(rt) << '\n' ;
}
return 0 ;
// code end.
}
KD-Tree 学习笔记的更多相关文章
- k-d tree 学习笔记
以下是一些奇怪的链接有兴趣的可以看看: https://blog.sengxian.com/algorithms/k-dimensional-tree http://zgjkt.blog.uoj.ac ...
- K-D Tree学习笔记
用途 做各种二维三维四维偏序等等. 代替空间巨大的树套树. 数据较弱的时候水分. 思想 我们发现平衡树这种东西功能强大,然而只能做一维上的询问修改,显得美中不足. 于是我们尝试用平衡树的这种二叉树结构 ...
- kd tree学习笔记 (最近邻域查询)
https://zhuanlan.zhihu.com/p/22557068 http://blog.csdn.net/zhjchengfeng5/article/details/7855241 KD树 ...
- 珂朵莉树(Chtholly Tree)学习笔记
珂朵莉树(Chtholly Tree)学习笔记 珂朵莉树原理 其原理在于运用一颗树(set,treap,splay......)其中要求所有元素有序,并且支持基本的操作(删除,添加,查找......) ...
- dsu on tree学习笔记
前言 一次模拟赛的\(T3\):传送门 只会\(O(n^2)\)的我就\(gg\)了,并且对于题解提供的\(\text{dsu on tree}\)的做法一脸懵逼. 看网上的其他大佬写的笔记,我自己画 ...
- Link Cut Tree学习笔记
从这里开始 动态树问题和Link Cut Tree 一些定义 access操作 换根操作 link和cut操作 时间复杂度证明 Link Cut Tree维护链上信息 Link Cut Tree维护子 ...
- 矩阵树定理(Matrix Tree)学习笔记
如果不谈证明,稍微有点线代基础的人都可以在两分钟内学完所有相关内容.. 行列式随便找本线代书看一下基本性质就好了. 学习资源: https://www.cnblogs.com/candy99/p/64 ...
- splay tree 学习笔记
首先感谢litble的精彩讲解,原文博客: litble的小天地 在学完二叉平衡树后,发现这是只是一个不稳定的垃圾玩意,真正实用的应有Treap.AVL.Splay这样的查找树.于是最近刚学了学了点S ...
- LSM Tree 学习笔记——本质是将随机的写放在内存里形成有序的小memtable，然后定期合并成大的table flush到磁盘
The Sorted String Table (SSTable) is one of the most popular outputs for storing, processing, and ex ...
- LSM Tree 学习笔记——MemTable通常用 SkipList 来实现
最近发现很多数据库都使用了 LSM Tree 的存储模型,包括 LevelDB,HBase,Google BigTable,Cassandra,InfluxDB 等.之前还没有留意这么设计的原因,最近 ...
随机推荐
- 注册并加入dn42网络的方法
简介 https://dn42.net/howto/Getting-started 注册要求: 一个24小时运行的linux/BSD设备 该设备必须支持创建隧道,例如GRE,OpenVpn,IPSec ...
- Python中heapq与优先队列【详细】
本文始发于个人公众号:TechFlow, 原创不易,求个关注 今天的文章来介绍Python当中一个蛮有用的库--heapq. heapq的全写是heap queue,是堆队列的意思.这里的堆和队列都是 ...
- 安卓开发实战-记账本APP（五）
今天将昨天剩余的bug修复,并且完成图标的美化,设置长按删除,模仿支付宝实现金额的动态增加. ①将昨天的布局进行了修改:之前是fragment,改成FrameLayout布局,不再设置name,进而在 ...
- javaIO编码详解
原创 输出流 有哪些构造方法可以在参数上设置编码格式 PrintStream(File file, String csn) PrintStream(String fileName, String cs ...
- mplayer使用心得[转]
一直在用mplayer,其他的播放器很少用.以下是我使用过程中的一些心得. 注意,下面用的路径都是在我的电脑上的路径,使用时请不要照抄!应该换成你的电脑上的正确路径. 一.首先还是讲安装方面的问题 ...
- PAT_B_PRAC_1003养兔子
题目描述 一只成熟的兔子每天能产下一胎兔子.每只小兔子的成熟期是一天. 某人领养了一只小兔子,请问第N天以后,他将会得到多少只兔子. 输入描述: 测试数据包括多组,每组一行,为整数n(1≤n≤90). ...
- 吴sir 讲Python之——Pycharm的安装教程 （一）
欢迎您进入老吴的博客,如有联系请加QQ群:1055524279 首先在Pycharm的官网下载Pycharm Pycharm官网链接:https://www.jetbrains.com/pycharm ...
- php扩展模块的安装
PHP的扩展模块安装 模块安装总则: 进入到ext/目录下对应的模块 执行/usr/local/php/bin/phpize 也就是执行一遍phpize生成编译文件 ./configure --wit ...
- Go语言实现：【剑指offer】复杂链表的复制
该题目来源于牛客网<剑指offer>专题. 输入一个复杂链表(每个节点中有节点值,以及两个指针,一个指向下一个节点,另一个特殊指针指向任意一个节点),返回结果为复制后复杂链表的head.( ...
- Linux中awk抽取包含某字段的整行日志
命令示例:awk '{if($0~"listAuths") print}' xxx.log 解释说明:抽取xxx.log整个日志文件中,包含“listAuths”的行,打印输出