python实现贝叶斯网络的概率推导（Probabilistic Inference）

写在前面

这是HIT2019人工智能实验三，由于时间紧张，代码没有进行任何优化，实验算法仅供参考。

实验要求

实现贝叶斯网络的概率推导（Probabilistic Inference）

具体实验指导书见github

这里首先给出代码

知识部分

关于贝叶斯网络的学习，我参考的是这篇博客

贝叶斯网络（belief network）

这篇博客讲述的虽然全面，但细节部分，尤其是贝叶斯网络概率推导的具体实现部分，一笔带过。然而本次实验的要求就是实现贝叶斯网络的概率推导，因此我在学习完这篇博客的基础上，又把老师发的ppt学了一遍，（由于ppt是英文的，一开始我是拒绝学的），最后又挑重点看了下博客和ppt，感觉豁然开朗。

因此如果没有学习过贝叶斯网络，建议按照我上面列出的顺序学习。

由于ppt较大，因此这里以网盘形式给出，提取码:cn3h，该ppt仅供个人学习参考，严禁以盈利形式传播

关于贝叶斯网络的概率推导，最重要的公式是以下这两个：

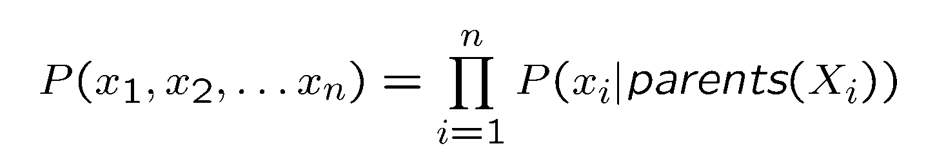
这两个公式具体什么意思，网上或者是ppt中都有讲解，这里不再赘述。重点在于这两个公式是完成本实验代码的核心公式，这一点我在完成实验之后才意识到，在之前学习ppt的时候，由于公式众多，并没有意识到这两个公式的重要性。

实验代码

代码所在的github地址已给出

需要注意的是，由于该实验指定了数据格式，因此代码完全是在指定数据格式要求下完成的，不具有普适性，因此实验代码仅供参考算法使用。

设计的cpt格式如下：

class cpt:
    def __init__(self, name, parents, probabilities):
        self.name = name
        self.parents = parents
        self.probabilities = probabilities

贝叶斯网络代码如下

from cpt import cpt

class BN:
    def __init__(self, nums, variables, graph, cpts):
        self.nums = nums
        self.variables = variables
        self.graph = graph
        self.cpts = cpts
        # 创建一个名字与编号的字典，便于查找
        index_list = [i for i in range(self.nums)]
        self.variables_dict = dict(zip(self.variables, index_list))
        # 计算全概率矩阵
        self.TotalProbability = self.calculateTotalProbability()

    def calculateProbability(self, event):
        # 分别计算待求变量个数k1和待消除变量个数k2，剩余的为条件变量个数
        k1 = self.count(event, 2)
        k2 = self.count(event, 3)

        probability = []
        for i in range(2**k1):
            p = 0
            for j in range(2**k2):
                index = self.calculateIndex(self.int2bin_list(i, k1), self.int2bin_list(j, k2), event)
                p = p + self.TotalProbability[index]
            probability.append(p)
        # 最后输出的概率矩阵的格式：先输出true，再输出false
        return list(reversed([x/sum(probability) for x in probability]))

    def calculateTotalProbability(self):
        # 全概率矩阵为一个1 * 2^n大小的矩阵，将列号转化为2进制，可表示事件的发生情况
        # 例如共有5个变量，则第7列的概率为p，表示事件00111（12不发生，345发生）发生的概率为p
        TotalProbability = [0 for i in range(2 ** self.nums)]
        for i in range(2 ** self.nums):
            p = 1
            binary_list = self.int2bin_list(i,self.nums)
            for j in range(self.nums):
                # 分没有父节点和有父节点的情况
                # 注意python float在相乘时会产生不精确的问题，因此每次相乘前先乘1000将其转化成整数相乘，最后再除回来
                if self.cpts[j].parents == []:
                    p = p * (self.cpts[j].probabilities[0][1-binary_list[j]] * 1000)
                else:
                    parents_list = self.cpts[j].parents
                    parents_index_list = [self.variables_dict[k] for k in parents_list]
                    index = self.bin_list2int([binary_list[k] for k in parents_index_list])
                    p = p * (self.cpts[j].probabilities[index][1 - binary_list[j]] * 1000)
            TotalProbability[i] = p / 10 ** (self.nums * 3)
        return TotalProbability

    def int2bin_list(self, a, b):
        # 将列号转化成指定长度的二进制数组
        # 下面两句话的含义：将a转化成二进制字符串，然后分割成字符串数组，再将字符串数组转化成整形数组
        # 若得到的整型数组长度不满足self.nums，则在前面补上相应的零
        binary_list = list(map(int, list(bin(a).replace("0b", ''))))
        binary_list = (b - len(binary_list)) * [0] + binary_list
        return binary_list

    def bin_list2int(self, b):
        # 将二进制的数组转化成整数
        result = 0
        for i in range(len(b)):
            result = result + b[len(b)-1-i] * (2 ** i)
        return result

    def calculateIndex(self, i, j, event):
        # 用于生成下标
        # 原理暂略
        index_list = []
        for k in range(len(event)):
            if event[k] == 2:
                index_list.append(i[0])
                del(i[0])
            elif event[k] == 3:
                index_list.append(j[0])
                del(j[0])
            else:
                index_list.append(event[k])

        return self.bin_list2int(index_list)

    def count(self, list, a):
        # 用于统计一个list中含有多少个指定的数字
        c = 0
        for i in list:
            if i == a:
                c = c + 1
        return c

该实验的主程序（包括读取指定数据文件的函数）如下：

import sys

from BN import BN
from cpt import cpt

# 读取文件并生成一个贝叶斯网络
def readBN(filename):
    f = open(filename, 'r')
    # 读取变量数
    nums = int(f.readline())
    f.readline()
    # 读取变量名称
    variables = f.readline()[:-1].split(' ')
    f.readline()
    # 读取有向图邻接表
    graph = []
    for i in range(nums):
        line = f.readline()[:-1].split(' ')
        graph.append(list(map(int, line)))
    f.readline()
    # 读取cpt表
    # 注意，文件中数据格式必须完全按照指定要求，不可有多余的空行或空格
    cpts = []
    for i in range(nums):
        probabilities = []
        while True:
            line = f.readline()[:-1].split(' ')
            if line != ['']:
                probabilities.append(list(map(float, line)))
            else:
                break
        CPT = cpt(variables[i], [], probabilities)
        cpts.append(CPT)
    f.close()
    # 根据邻接表为每个节点生成其父亲节点
    # 注意，这里父亲节点的顺序是按照输入的variables的顺序排列的，不保证更换测试文件时的正确性
    for i in range(nums):
        for j in range(nums):
            if graph[i][j] == 1:
                cpts[j].parents.append(variables[i])

    # 测试父节点生成情况
    # for i in range(nums):
    #     print(cpts[i].parents)
    bayesnet = BN(nums, variables, graph, cpts)
    return bayesnet

# 读取需要求取概率的命令
def readEvents(filename, variables):
    # 条件概率在本程序中的表示：
    # 对变量分类，2表示待求的变量，3表示隐含的需要被消去的变量，0和1表示条件变量的false和true
    # 例如变量为[Burglar, Earthquake, Alarm, John, Mary]
    # 待求的条件概率为P(Burglar | John=true, Mary=false)，则event为[2, 3, 3, 1, 0]
    f = open(filename, 'r')
    events = []
    while True:
        line = f.readline()
        event = []
        if line == "\n":
            continue
        elif not line:
            break
        else:
            for v in variables:
                index = line.find(v)
                if index != -1:
                    if line[index+len(v)] == ' ' or line[index+len(v)] == ',':
                        event.append(2)
                    elif line[index+len(v)] == '=':
                        if line[index+len(v)+1] == 't':
                            event.append(1)
                        else:
                            event.append(0)
                else:
                    event.append(3)
            # 检查文本错误
            if len(event) != len(variables):
                sys.exit()
            events.append(event)
    return events

# 主程序
filename1 = "burglarnetwork.txt"
bayesnet = readBN(filename1)
filename2 = "burglarqueries.txt"
events = readEvents(filename2, bayesnet.variables)
for event in events:
    print(bayesnet.calculateProbability(event))

知识总结

这一部分主要记录在实验过程中参考的博客，方便之后复习

由于没有系统学过python，其中有挺多都是python基本技巧的，看来以后还要系统学一遍

python中判断readline读到文件末尾

这篇博客参考的是读文件时如何判断读完

python 字符串和整数，浮点型互相转换

这篇博客参考的是如何将从文件读进来的文本转化成数据

python-使用列表创建字典

这篇博客参考的是用list创建字典的方式

python在字符串中查找字符

在Python中，如何将一个字符串数组转换成整型数组

Python-8、Python如何将整数转化成二进制字符串

这三篇博客同样是在处理读入数据时参考的

Python3浮点型（float）运算结果不正确处理办法

由于多个浮点数的概率在连乘的时候，导致出现了较大误差，因此查了这篇博客，不过最后没有使用Decimal模块，而是直接乘1000再除1000解决了。

Python 技巧（三）—— list 删除一个元素的三种做法

python numpy查询数组是否有某个数的总个数

这篇博客，我试了一下发现不可以，报错说不可以对布尔类型求和，恐怕是python版本的问题吧，这个我暂时没有深究，自己写了一个count函数

python list中数字与一个数相乘

对于list中一个数字与一个数相乘的方法，网上普遍给出的另一种方法是用numpy库，其生成的数组可以直接与数相乘。然而由于我全程没有用到numpy，不想在这个地方单独用个numpy，所以采用了本篇博客中的方法。

python反转列表的三种方式

由于实验指导书指定的输出结果与我算出来的相反，因此翻转了一次列表

实验总结

用一句话总结该实验的作用：使我对于贝叶斯网络的概率推导过程理解的更加透彻

做完实验才意识到如果没有手推几个贝叶斯网络的概率推导，那几乎相当于没有学，要是放到考试绝对写不出来（想起了之前听觉考试，平时没有练习过手推隐马尔科夫，导致考试的时候给了一个很简单的HMM，最后由于太不熟练导致时间不足而没有写完）

整个实验过程比较顺畅，总时间大致8小时左右，其中写代码时间很短，全程几乎没有遇到bug，花时间的地方在于如何设计表示条件概率。这个东西花了我特别长的时间，最后的形式个人感觉不是特别简洁，但是放在程序里还是挺好用的。