HDU-6070 Dirt Ratio(二分+线段树+分数规划)
(有任何问题欢迎留言或私聊 && 欢迎交流讨论哦
目录
题意:传送门
原题目描述在最下面。
求\(sum/len\)最小值。\(sum\)是一段区间内不同数字的个数,\(len\)是这段区间的长度。
思路:
首先预处理出每个数上一次出现的位置\(pre[i]\)和最后一次出现的位置\(lst[i]\)。这个操作在静态求区间内不同数的个数和动态求区间内不同数的个数都有用到。
法一:
二分答案\(mid\)。枚举序列,每加入一个数就在\(pre[i]-i\)区间加一,因为在以\(i\)为右端点的所有区间内,这么区间多了一个新数字。
对于\(sum/len\leq mid\; \rightarrow sum - len * mid \leq 0\)。我们已经处理了\(sum\),对于\(len*mid\),就在解决每次插入一个数后,在\(1-i\)区间减去\(k\)。最后查询区间最小值,如果小于\(0\)则此\(mid\)符合还可以更小。
因为我们每加入一个数后,查询的是以\(i\)为右端点的区间最小值,所以很自然的就要\(1-i\)每次减去\(k\)。这样才符合上述表达式。感觉画个图更好理解。
法二:
化简表达式为:$sum(L,R)+Lmid \leq Rmid $
\(sum\)的更新和上面一样,但是左边多了一项\(l*mid\)。
怎么办呢?解决方法就是在线段树的每个端点处的值初始化为\(l*mid\)(\(l\)是到\(1\)的距离)。
然后每此更新完后查询区间最小值\(mmin\),如果\(mmin\leq i*mid\)则此\(mid\)符合还可以更小
AC代码:
#include<bits/stdc++.h>#define lson rt<<1#define rson rt<<1|1#define mme(a,b) memset((a),(b),sizeof((a)))using namespace std;const int N = 1e5+7;int n;int lst[N],pre[N],ar[N];double sum[N<<2],lazy[N<<2];void push_up(int rt){sum[rt]=min(sum[lson],sum[rson]);}void push_down(int rt){if(lazy[rt]){lazy[lson]+=lazy[rt];lazy[rson]+=lazy[rt];sum[lson]+=lazy[rt];sum[rson]+=lazy[rt];lazy[rt]=0;}}void update(int L,int R,int l,int r,double c,int rt){if(L<=l&&r<=R){sum[rt] += c;lazy[rt] += c;return;}push_down(rt);int mid = (l+r)>>1;if(L<=mid) update(L,R,l,mid,c,lson);if(R>mid) update(L,R,mid+1,r,c,rson);push_up(rt);}double query(int L,int R,int l,int r,int rt){if(L<=l&&r<=R){return sum[rt];}push_down(rt);int mid = (l+r)>>1;double sum=n;if(L<=mid) sum = min(sum, query(L,R,l,mid,lson));if(R>mid) sum = min(sum, query(L,R,mid+1,r,rson));push_up(rt);return sum;}/*151 2 1 2 3sum/len最小值sum/len <= midsum - len*mid <= 0sum 区间不同数字的个数len 区间长度*/bool ok(double e){mme(sum,0);mme(lazy,0);for(int i=1;i<=n;++i){update(pre[i]+1,i,1,n,1,1);update(1,i,1,n,-e,1);if(query(1,i,1,n,1)<=0)return 1;}return false;}int main(){int tim;scanf("%d",&tim);while(tim--){scanf("%d",&n);mme(lst,0);mme(pre,0);for(int i=1;i<=n;++i){scanf("%d",&ar[i]);pre[i]=lst[ar[i]];lst[ar[i]]=i;}double l=0,r=1,mid;for(int i=0;i<20;++i){mid=(l+r)/2;if(ok(mid))r=mid;else l=mid;}printf("%.5f\n", r);}return 0;}
####原题目描述:
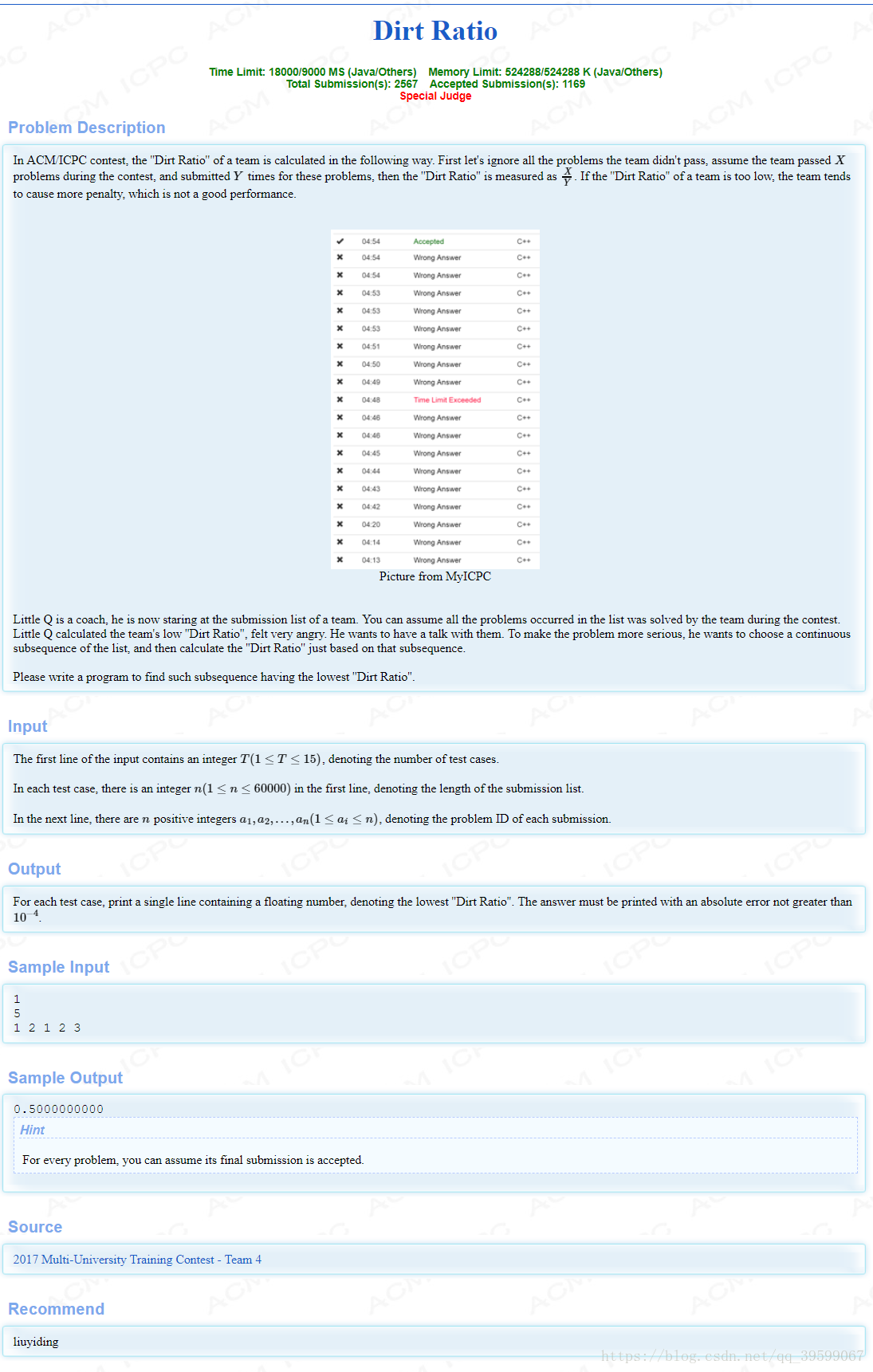
HDU-6070 Dirt Ratio(二分+线段树+分数规划)的更多相关文章
- 2017ACM暑期多校联合训练 - Team 4 1004 HDU 6070 Dirt Ratio (线段树)
题目链接 Problem Description In ACM/ICPC contest, the ''Dirt Ratio'' of a team is calculated in the foll ...
- HDU 6070 Dirt Ratio(线段树)
Dirt Ratio Time Limit: 18000/9000 MS (Java/Others) Memory Limit: 524288/524288 K (Java/Others)Tot ...
- hdu6070 Dirt Ratio 二分+线段树
/** 题目:hdu6070 Dirt Ratio 链接:http://acm.hdu.edu.cn/showproblem.php?pid=6070 题意:给定n个数,求1.0*x/y最小是多少.x ...
- HDU 6070 - Dirt Ratio | 2017 Multi-University Training Contest 4
比赛时会错题意+不知道怎么线段树维护分数- - 思路来自题解 /* HDU 6070 - Dirt Ratio [ 二分,线段树 ] | 2017 Multi-University Training ...
- K-th occurrence HDU - 6704 (后缀数组+二分线段树+主席树)
大意: 给定串s, q个询问(l,r,k), 求子串s[l,r]的第kk次出现位置. 这是一篇很好的题解: https://blog.csdn.net/sdauguanweihong/article/ ...
- HDU 6070 Dirt Ratio(分数规划+线段树)
http://acm.hdu.edu.cn/showproblem.php?pid=6070 题意: 找出一个区间,使得(区间内不同数的个数/区间长度)的值最小,并输出该值. 思路: 因为是要求$\f ...
- hdu 6070 Dirt Ratio 线段树+二分
Dirt Ratio Time Limit: 18000/9000 MS (Java/Others) Memory Limit: 524288/524288 K (Java/Others)Spe ...
- hdu 6070 Dirt Ratio
题 OvO http://acm.hdu.edu.cn/showproblem.php?pid=6070 (2017 Multi-University Training Contest - Team ...
- [WC2010]重建计划(长链剖分+线段树+分数规划)
看到平均值一眼分数规划,二分答案mid,边权变为w[i]-mid,看是否有长度在[L,R]的正权路径.设f[i][j]表示以i为根向下j步最长路径,用长链剖分可以优化到O(1),查询答案线段树即可,复 ...
随机推荐
- docker的备份和迁移
备份与迁移 容器保存为镜像 我们可以通过以下命令将容器保存为镜像 docker commit pyg_nginx mynginx pyg_nginx是容器名称 mynginx是新的镜像名称 此镜像的内 ...
- eclipse中svn的各种图标详解
参考:http://blog.sina.com.cn/s/blog_637810b101018xw0.html - 已忽略版本控制的文件.可以通过Window → Preferences → Team ...
- shell重定向的顺序问题
三个默认的文件描述符 0: stdin(标准输入) 1: stdout(标准输出) 2: stderr(标准错误输出) 系统中这3个文件描述符所对应的文件: 重定向顺序 示例脚本 echo " ...
- Openstack组件部署 — Netwotking service组件介绍与网络基本概念
目录 目录 前文列表 Openstack Networking serivce 基本的Neutron概念 Neutron的抽象对象 网络networks 子网subnets 路由器routers 端口 ...
- Address already in use: JVM_Bind 8083端口被占用的几个解决办法
运行Tomcat时若出现Address already in use: JVM_Bind 端口被占用,一般使用下面几个办法可以解决: 假设端口为8083 1.启动cmd, 执行命令netstat -a ...
- 3. 初识jmeter及JDK安装
jmeter 介绍 Apache JMeter™应用程序是开源软件,100%纯Java应用程序,旨在加载测试功能行为和测量性能.它最初是为测试Web应用程序而设计的,但后来扩展到其他测试功能. Jme ...
- Android Telephony分析(七) ---- 接口扩展(异步转同步)
本文是基于上一篇<Android Telephony分析(六) —- 接口扩展(实践篇)>来写的.上一篇介绍的接口扩展的方法需要实现两部分代码:1. 从APP至RIL,发送请求:2. 从R ...
- ActionContext 与 ServletActionContext获取Session的异同
1. ActionContext 在Struts2开发中,除了将请求参数自动设置到Action的字段中,我们往往也需要在Action里直接获取请求(Request)或会话(Session)的一些信息, ...
- 7-MySQL-Ubuntu-操作数据表的基本操作(二)
修改数据表的结构 (1)向数据表中添加新的字段 alter table 表名 add 字段名 类型及约束; (2)修改字段的属性(字段的数据类型和约束) 注:modify不能修改字段名,只能修改字段 ...
- 如果通过cookies和localStorage取值?
1. getCook : 设定setCookie值 let setCookie = setCookie('wan',data,7); function setCookie(c_name,value,e ...
