理解最短路径-Dijkstra算法

最短路径—Dijkstra算法和Floyd算法

透彻理解迪杰斯特拉算法

Dijkstra算法的使用条件：图中不存在负权边。

---------------------------有待验证------------------------

Dijkstra 算法，用于对有权图进行搜索，找出图中两点的最短距离，既不是DFS搜索，也不是BFS搜索。 
把Dijkstra 算法应用于无权图，或者所有边的权都相等的图，Dijkstra 算法等同于BFS搜索。

--------------------------------------------------------------

算法思想描述：设G=(V,E)是一个带权有向图，把图中顶点集合V分成两组，第一组为已求出最短路径的顶点集合（用S表示，初始时S中只有一个源点，以后每求得一条最短路径 , 就将加入到集合S中，直到全部顶点都加入到S中，算法就结束了），第二组为其余未确定最短路径的顶点集合（用U表示），按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中，总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外，每个顶点对应一个距离，S中的顶点的距离就是从v到此顶点的最短路径长度，U中的顶点之间的距离，是从v到此顶点(只包括S中的顶点为中间顶点)的当前最短路径长度。

注意：对算法思想描述中的加粗字体的理解非常重要，后面会在有权图的最短路径求解步骤中给出理由和陷阱。

原博客中有图和步骤表格，这里不再进行复制，有兴趣的同学可以移步文章开头链接，这里重新用另外一张图进行说明

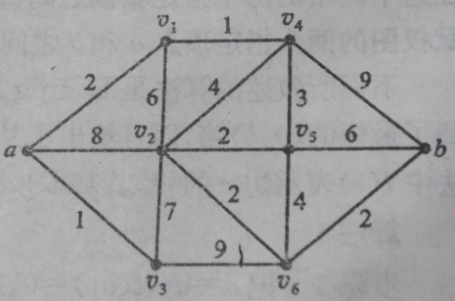
步骤	S集合	U集合
1	选入a，此时S=<a> 此时最短路径a→a=0 以a为中间点，从a开始找	U=<v1、v2、v3、v4、v5、v6、b> a→v1=2 a→v2=8 a→v3=1 a→其他U中的顶点=∞ 发现a→v3=1权值最短
2	选入v3，此时S=<a、v3> 此时最短路径a→a=0，a→v3=1 以v3为中间点，从a→v3=1这条最短路径开始找	U=<v1、v2、v4、v5、v6、b> a→v3→v2=8（比上面第一步的a→v2=8相等，保持不变） a→v3→v6=10 a→v3→其他U中的顶点=∞（这里有a→v3→v1=∞， 比第一步中的a→v1=2要长），此时a到v1的权值更改为a→v1=2 发现a→v1=2权值最短
3	选入v1，此时S=<a、v3、v1> 此时最短路径a→a=0，a→v3=1，a→v1=2 以v1为中间点，从a→v1=2这条最短路径开始找	U=<v2、v4、v5、v6、b> a→v1→v2=8（比上面第一步的a→v2=8相等，保持不变） a→v1→v4=3 a→v1→其他U中的顶点=∞ 发现a→v1→v4=3权值最短
4	选入v4，此时S=<a、v3、v1、v4> 此时最短路径a→a=0，a→v3=1，a→v1=2， a→v1→v4=3 以v4为中间点，从a→v1→v4=3这条最短路径开始找	U=<v2、v5、v6、b> a→v1→v4→v2=7（比上面第一步的a→v2=8要短） 此时a到v2的权值更改为a→v1→v4→v2=7 a→v1→v4→v5=6 a→v1→v4→b=12 a→v1→v4→其他U中的顶点=∞ 发现a→v1→v4→v5=6权值最短
5	选入v5，此时S=<a、v3、v1、v4、v5> 此时最短路径 a→a=0，a→v3=1，a→v1=2， a→v1→v4=3，a→v1→v4→v5=6 以v5为中间点，从a→v1→v4→v5=6这条最短路径 开始找	U=<v2、v6、b> a→v1→v4→v5→v2=8（比上面第四步的a→v1→v4→v2=7要长） 此时a到v2的权值更改为a→v1→v4→v2=7 a→v1→v4→v5→v6=10 a→v1→v4→v5→b=12 发现a→v1→v4→v2=7权值最短
6	选入v2，此时S=<a、v3、v1、v4、v5、v2> 此时最短路径 a→a=0，a→v3=1，a→v1=2， a→v1→v4=3，a→v1→v4→v5=6， a→v1→v4→v2=7 以v2为中间点，从a→v1→v4→v2=7这条最短路径 开始找	U=<v6、b> a→v1→v4→v2→v6=9 a→v1→v4→v2→其他U中的顶点=∞ 发现a→v1→v4→v2→v6=9权值最短
7	选入v6，此时S=<a、v3、v1、v4、v5、v2、v6> 此时最短路径a→a=0，a→v3=1，a→v1=2， a→v1→v4=3，a→v1→v4→v5=6， a→v1→v4→v2=7，a→v1→v4→v2→v6=9 以v6为中间点，从a→v1→v4→v2→v6=9这条最短路径 开始找	U=<v6、b> a→v1→v4→v2→v6→b=11 发现a→v1→v4→v2→v6→b=11权值最短
8	选入b，此时S=<a、v3、v1、v4、v5、v2、v6、b> 此时最短路径a→a=0，a→v3=1，a→v1=2， a→v1→v4=3，a→v1→v4→v5=6， a→v1→v4→v2=7，a→v1→v4→v2→v6=9， a→v1→v4→v2→v6→b=11	U集合已空，算法结束。

其中每次步骤执行时，从S集合确定中间点和开始查找的最短路径，依次遍历U集合中的 点，遵循的原则是，按最短路径长度的递增次序依次把第二组的顶点加入S，保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度，在寻找最短权值时要注意查找前面步骤是否已经查找记录过。