动态规划——DP算法（Dynamic Programing）

一、斐波那契数列（递归VS动态规划）

1、斐波那契数列——递归实现（python语言）——自顶向下

递归调用是非常耗费内存的，程序虽然简洁可是算法复杂度为O(2^n)，当n很大时，程序运行很慢，甚至内存爆满。

 def fib(n):
     #终止条件，也就是递归出口
     if n == 0 or n == 1:
         return 1
     else:
         #递归条件
         return (fib(n-1) + fib(n - 2))

2、斐波那契数列——动态规划实现（python语言）——自底向上

动态规划——将需要重复计算的问题保存起来，不需要下次重新计算。对于斐波那契数列，算法复杂度为O（n）。

 def dp_fib(n):
     #初始化一个数组，用于存储记录计算的结果。
     res = [None] * (n + 1)
     #前两项设置为1。
     res[0] = res[1] = 1
     #自底向上，将计算结果存入数组内。
     for i in range(2, (n + 1)):
         res[i] = res[i-1] + res[i-2]
     return res[n]

3、方法概要

　　（1）构造一个公式，它表示一个问题的解是与它的子问题的解相关的公式：

　　　　　

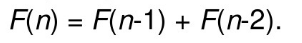
　　（2）为这些子问题做索引，以便于它们能够在表中更好的存储与检索（用数组存储）。

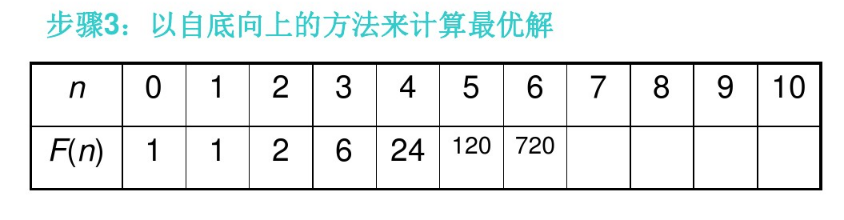
　　（3）以自底向上的方法来填写这个表格；首先填写最小的子问题的解。

　　（4）这就保证了当我们解决一个特殊的子问题时，可以利用比它更小的所有可利用的子问题的解。

总之，因为在上世纪40年代（计算机普及很少时），这些规划设计是与“列表”方法相关的，因此被称为动态规划——Dynamic Programing。

二、动态规划算法——思想简介

1、DP算法思想

　　（1）将待求解的问题分解称若干个子问题，并存储子问题的解而避免计算重复的子问题，并由子问题的解得到原问题的解。

　　 （2）动态规划算法通常用于求解具有某种最有性质的问题。

　　 （3）动态规划算法的基本要素：最优子结构性质和重叠子问题。

　　　　　　最优子结构性质：问题的最优解包含着它的子问题的最优解。即不管前面的策略如何，此后的决策必须是基于当前状态（由上一次的决策产生）的最优决策。

　　　　　　重叠子问题：在用递归算法自顶向下解问题时，每次产生的子问题并不总是新问题，有些问题被反复计算多次。对每个子问题只解一次，然后将其解保存起来，

　　　　　　　　　　　　以后再遇到同样的问题时就可以直接引用，不必重新求解。

2、DP算法——解决问题的基本特征

　　（1）动态规划一般求解最值（最优、最大、最小、最长）问题；

　　 （2）动态规划解决 的问题一般是离散的，可以分解的（划分阶段的）。

　　 （3）动态规划结局的问题必须包含最优子结构，即可以有（n-1）的最优推导出n的最优。

3、DP算法——解决问题的基本步骤

　　动态规划算法的四个步骤：

　　　　（1）刻画最优解的结构特性。（一维、二维、三维数组）；

　　　　（2）递归的定义最优解。（状态转移方程）

　　　　（3）以自底向上的方法来计算最优解。

　　　　（4）从计算得到的解来构造一个最优解。

 4、求解例子——求阶乘 n!

 #递归实现求阶乘
 def multiply(n):
     if n == 0 or n == 1:
         return 1
     return n * multiply(n -1)

 #动态规划实现求阶乘
 def dp_multiply(n):
     temp = [None] * (n + 1)
     temp[0] = 1
     temp[1] = 1
     for i in range(2, n + 1):
         temp[i] = i * temp[i - 1]
     return temp[n]

 三、动态规划——常见例题

1、求解最长不降子序列

　　（1）方法一：普通方法，算法复杂度为O（n^2）。

　　　　　　假设原始的数列为数组 a

　　　　　　分析：

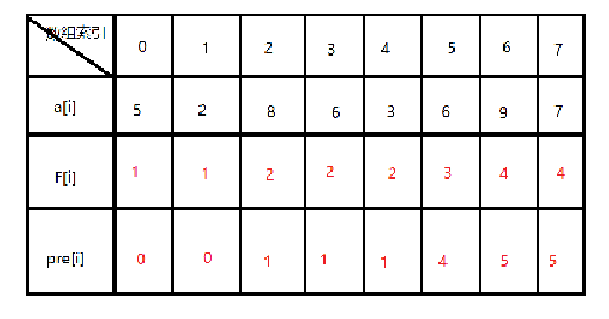
　　　　　　　　刻画结构特性：用F[ i ] 表示前 i 项最长不下降子序列的长度；

　　　　　　　　状态转移方程：如果a [ i ] >=a [ j ],  F[i] = max(F[i], F[j] + 1)  其中，0 <= j < i

　　　　　　　　数据存储：自底向上求解最小子结构最优解存入数组

其中，pre[ i ]表示以元素a [ i ] 为结尾的最长不降序列的前一个元素索引（也就是以a[i]结尾的最长不降序列的倒数第二个元素）。存储这个值是为了方便输出最长的不降序列。

 def Longest_Increaseing(a):
     F = [1] * len(a)
     pre = [0] * len(a)
     for i in range(1, len(a)):
         for j in range(i):
             if a[i] >= a[j]:
                 F[i] = max(F[i], F[j] + 1)
                 pre[i] = j
     return F, pre
 a = [5,2,8,6,3,6,9,7]
 F, pre = Longest_Increaseing(a)

#这里只是能获得两个数组，其中F[i]的最大值就是最长不降序列的长度。

接下来，输出最长的不降序列的元素值，请看下面的代码：

 def Longest_Increaseing(a):
     F = [1] * len(a)
     pre = [0] * len(a)
     for i in range(1, len(a)):
         for j in range(i):
             if a[i] >= a[j]:
                 F[i] = max(F[i], F[j] + 1)
                 pre[i] = j
     return F, pre
 a = [5,2,8,6,3,6,9,7]
 F, pre = Longest_Increaseing(a)

 #最长序列的索引
 k = F.index(max(F))
 #输出序列的列表
 result = [None] * F[k]
 flag = True
 Len = F[k]
 while flag:
     result[Len - 1] = a[k]
     k = pre[k]
     if k == 0:
         flag = False
     Len -= 1
 print(result)

#输出结果：[2, 3, 6, 9]

　　（2）方法二：时间复杂度为O（n * log(n)）

　　　　参考博文：最长不下降子序列 NlogN && 输出序列       https://www.cnblogs.com/milky-w/p/8431333.html

2、求解最长的公共子序列

求解最长公共子序列代码如下（python语言）：

 import numpy as np
 def LCS(str1, str2):
     #获取两个序列的长度
     m = len(str1)
     n = len(str2)
     #生成一个存储计算子问题的二位矩阵，并将元素初始化为0。
     #这个矩阵的尺寸比两个序列的尺寸分别大1个单位。
     #对于这个矩阵，第一行和第一列元素值必然为0。
     #C[i][j]的含义是：Xi = （x1, x2, x3,..., xi）和Yj = （y1, y2, x3,..., yj）的最长公共子序列
     C = np.zeros((m+1, n+1), dtype=int)
     b = np.zeros((m+1, n+1), dtype=int)

     for i in range(1, m+1):
         for j in range(1, n+1):
             #请注意这里为什么是i-1和j-1，因为其实C[1][1]表示的是
             # 两个序列的首个元素的最长公共子序列，对应的是str1[0]和str2[0]
             if str1[i-1] == str2[j-1]:
                 C[i][j] = C[i-1][j-1] + 1
                 b[i][j] = 1      #表示对角线方向
             else:
                 if C[i][j-1] <= C[i-1][j]:
                     b[i][j] = 2     #表示朝上方向
                 else:
                     b[i][j] = 3     #表示朝左方向
                 C[i][j] = max(C[i][j-1], C[i-1][j])
     return C, b

 test1 = ['b', 'd','c', 'a', 'b', 'a']
 test2 = ["a","b","c","b","d","a","b"]
 a, b = LCS(test2, test1)

 print(a)
#矩阵a存储的是公共子序列的长度，最大值就是最大公共子序列的长度

[[0 0 0 0 0 0 0]
[0 0 0 0 1 1 1]
[0 1 1 1 1 2 2]
[0 1 1 2 2 2 2]
[0 1 1 2 2 3 3]
[0 1 2 2 2 3 3]
[0 1 2 2 3 3 4]
[0 1 2 2 3 4 4]]

 print(b)
#这里： 1表示对角线方向、2表示朝上、3表示朝左，主要是为了求具体的子序列用的。

[[0 0 0 0 0 0 0]
[0 2 2 2 1 3 1]
[0 1 3 3 2 1 3]
[0 2 2 1 3 2 2]
[0 1 2 2 2 1 3]
[0 2 1 2 2 2 2]
[0 2 2 2 1 2 1]
[0 1 2 2 2 1 2]]

接下来是输出最长公共子序列：

 import numpy as np
 def LCS(str1, str2):
     #获取两个序列的长度
     m = len(str1)
     n = len(str2)
     #生成一个存储计算子问题的二位矩阵，并将元素初始化为0。
     #这个矩阵的尺寸比两个序列的尺寸分别大1个单位。
     #对于这个矩阵，第一行和第一列元素值必然为0。
     #C[i][j]的含义是：Xi = （x1, x2, x3,..., xi）和Yj = （y1, y2, x3,..., yj）的最长公共子序列
     C = np.zeros((m+1, n+1), dtype=int)
     b = np.zeros((m+1, n+1), dtype=int)

     for i in range(1, m+1):
         for j in range(1, n+1):
             #请注意这里为什么是i-1和j-1，因为其实C[1][1]表示的是
             # 两个序列的首个元素的最长公共子序列，对应的是str1[0]和str2[0]
             if str1[i-1] == str2[j-1]:
                 C[i][j] = C[i-1][j-1] + 1
                 b[i][j] = 1      #表示对角线方向
             else:
                 if C[i][j-1] <= C[i-1][j]:
                     b[i][j] = 2     #表示朝上方向
                 else:
                     b[i][j] = 3     #表示朝左方向
                 C[i][j] = max(C[i][j-1], C[i-1][j])
     return C, b

 def Print_Lcs(b, X, i , j):
     if i == 0 or j == 0:
         return
     if b[i][j] == 1:
         Print_Lcs(b, X, i-1, j-1)
         print(X[i-1])  #为什么是i-1，因为b矩阵的行比X的行长一个单位，而且只输出相等的值，表示公共元素。
     elif b[i][j] == 2:
         Print_Lcs(b, X, i-1, j)
     else:
         Print_Lcs(b, X, i, j-1)

 if __name__ == '__main__':
     test1 = ['b', 'd','c', 'a', 'b', 'a']
     test2 = ["a","b","c","b","d","a","b"]
     a, b = LCS(test2, test1)
     Print_Lcs(b, test2, 7, 6)

#输出的结果是:  b、c、b、a  。(请注意这里结果不唯一，因为最长子序列长度为4， 存在三个序列长度为4的子序列)