@NOI模拟2017.06.30 - T1@ Left

目录

• @description@
• @solution@
• @accepted code@
• @details@

---

@description@

JOHNKRAM 最近在研究排序网络，但他发现他不会制作比较器，于是他用交换器来代替比较器。

一个交换器有两个输入端 x, y 和两个输出端 x′, y′​​。如果交换器处于关闭状态，则 x 收到的信号会从 x′ 发出，y 收到的信号会从 y′ 发出。如果交换器处于开启状态，则 x 收到的信号会从 y′ 发出，y 收到的信号会从 x' 发出。

JOHNKRAM 设计了这样一个递归定义的网络：

（1）1阶网络就是一个交换器。

（2）n (n>1) 阶网络的第一排是 2^(n−1) 个交换器，接下来是两个 n−1 阶网络,最后一排也是2^(n−1) 个交换器。

将第一排的输出端和第二排的输入端分别从左到右标号为 0∼2^n−1，第一排的 i 输出端连接到第二排的 i>>1 输入端，其中 >> 指n位二进制数的循环右移。

类似，将倒数第一排的输入端和倒数第二排的输出端分别从左到右标号为 0∼2^n−1，倒数第二排的 i 输出端连接到倒数第一排的 i<<1 输入端，其中 << 指 n 位二进制数的循环左移。

一个3阶的网络如下图所示：

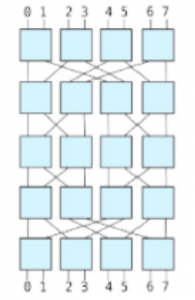
JOHNKRAM 通过开关交换器来调整网络。现在他对一个 n 阶网络的 2^n 个输入端分别输入了一个数，第 i (0≤i<2^n) 个输入端输入的是 i。然后他给出了一个长度为 2^n 的排列 p。他希望你给出一种网络的状态，使得第 i (0≤i<2^n) 个输出端输出的是 pi。

input

包括不超过 10 组数据，每组数据包含两行。

第一行包含一个整数 n，其中 1≤n≤13。

第二行 2^n 个整数表示排列 p。

输入以 0 结尾。

output

如果无解，输出 -1。

否则输出 2n - 1 行，每行包含 2^(n-1) 位的二进制数，表示网络的状态。如果那一位的交换器开启则为 1，否则为 0。

如果有多解，输出字典序最小的解。

每组数据输出之间用空行隔开。

sample input

2

3 2 1 0

3

3 7 4 0 2 6 1 5

0

sample output

00

11

11

0011

0000

0110

1111

1101

@solution@

递归定义的结构可以使用递归求解（要用递归打败递归！）

在 n 阶网络中，不难发现对于第一行的交换器而言，它的左输出端只会连接到左边的 n-1 阶网络，右输出端只会连接到右边的 n-1 阶网络。同理对最后一行的交换器，它的左输入端只会连接到左边的 n-1 阶网络，右输入端只会连接到右边的 n-1 网络。

同时，我们发现如果开启第一行的交换器，只会影响输入端的两个数哪一个进左边的网络，哪一个进右边的网络。最后一行同理。

记 a[i] 表示第一行第 i 个交换器是否打开（打开为 1，否则为 0），b[i] 表示最后一行第 i 个交换器是否打开。

记 c[i] 表示数 i 在第一行哪个交换器输入， d[i] 表示数 i 在最后一行哪个交换器输出。

记 e[i] 表示数 i 在第一行的交换器的左边输入还是右边输入（左边为 0，右边为 1），f[i] 表示数 i 在最后一行的交换器的左边输入还是右边输入。

则如果一个网络合法，对于每一个数 i，一定满足 e[i] xor f[i] xor a[c[i]] xor b[d[i]] = 0。

因为是求字典序最小的解，所以可以在第一行从左到右枚举每一个交换器是 0 还是 1，再通过上面那个式子 bfs 进行合法性判定。

决定好了第一行与最后一行，就可以递归解决两个 n-1 阶的子问题。总时间复杂度 O(2^(2n))。

题目虽然说无解输出 -1，但实际上总是有解，可以通过归纳法证明（虽然我代码还是判了无解的）。

为了实现简单可以总是将第一行的输入端调成 0 1 2 3…… 的形式。

@accepted code@

#include<cstdio>
#include<queue>
using namespace std;
const int MAXN = 13;
int x[1<<MAXN], y[1<<MAXN], tp;
int ans[MAXN<<1][1<<MAXN];
int a[1<<MAXN], n, s, t, u;
int tmp1[1<<MAXN], tmp2[1<<MAXN], tmp3[1<<MAXN], tmp4[1<<MAXN];
int stk3[1<<MAXN], stk4[1<<MAXN], tp3, tp4;
queue<int>que;
void restore() {
	while( tp3 ) tmp3[stk3[tp3--]] = -1;
	while( tp4 ) tmp4[stk4[tp4--]] = -1;
}
bool check(int x, int y) {
	stk3[++tp3] = x, tmp3[x] = y;
	que.push(x<<1), que.push(x<<1|1);
	while( !que.empty() ) {
		int f = que.front(); que.pop();
		if( f < (u<<1) ) {
			if( tmp4[tmp2[f]>>1] != -1 ) {
				if( (tmp3[f>>1] == tmp4[tmp2[f]>>1]) != ((f&1) == (tmp2[f]&1)) ) {
					restore();
					return false;
				}
			}
			else {
				stk4[++tp4] = tmp2[f]>>1;
				tmp4[tmp2[f]>>1] = (f&1)^(tmp2[f]&1)^tmp3[f>>1];
				que.push((tmp2[f]^1) + (u<<1));
			}
		}
		else {
			f -= (u<<1);
			if( tmp3[tmp1[f]>>1] != -1 ) {
				if( (tmp3[tmp1[f]>>1] == tmp4[f>>1]) != ((f&1) == (tmp1[f]&1)) ) {
					restore();
					return false;
				}
			}
			else {
				stk3[++tp3] = tmp1[f]>>1;
				tmp3[tmp1[f]>>1] = (f&1)^(tmp1[f]&1)^tmp4[f>>1];
				que.push(tmp1[f]^1);
			}
		}
	}
	tp3 = tp4 = 0;
	return true;
}
int main() {
	freopen("left.in", "r", stdin);
	freopen("left.out", "w", stdout);
	while( scanf("%d", &n) == 1 && n ) {
		s = (1<<n), t = (s>>1);
		for(int i=0;i<s;i++)
			scanf("%d", &a[i]);
		bool flag = true;
		for(int i=n;i>=1;i--) {
			/*printf("| ");
			for(int j=0;j<s;j++)
				printf("%d ", a[j]);
			puts("");*/
			u = (1<<(i-1));
			for(int j=0;j<t;j+=u) {
				for(int k=0;k<u;k++) {
					tmp1[k<<1] = a[(j+k)<<1], tmp1[k<<1|1] = a[(j+k)<<1|1];
					tmp2[tmp1[k<<1]] = k<<1, tmp2[tmp1[k<<1|1]] = k<<1|1;
					tmp3[k] = tmp4[k] = -1;
				}
				for(int k=0;k<u;k++) {
					if( tmp3[k] == -1 ) {
						if( !check(k, 0) && !check(k, 1) ) {
							flag = false;
							break;
						}
					}
				}
				for(int k=0;k<u;k++)
					 ans[n-i+1][j+k] = tmp3[k], ans[n+i-1][j+k] = tmp4[k];
				for(int k=0;k<u;k++) {
					if( !tmp4[k] ) a[(j<<1)+k] = (tmp1[k<<1]>>1), a[(j<<1)+k+u] = (tmp1[k<<1|1]>>1);
					else a[(j<<1)+k] = (tmp1[k<<1|1]>>1), a[(j<<1)+k+u] = (tmp1[k<<1]>>1);
				//	printf(". %d %d\n", j+k, j+k+u);

			/*printf("| ");
			for(int j=0;j<s;j++)
				printf("%d ", a[j]);
			puts("");*/
				}
				if( !flag ) break;
			}
			if( !flag ) break;
		}
		if( !flag ) puts("-1");
		else {
			for(int i=1;i<=2*n-1;i++) {
				for(int j=0;j<t;j++)
					printf("%d", ans[i][j]);
				puts("");
			}
		}
		puts("");
	}
}

@details@

康复计划 - 8。

切水题是真_的爽~

有一个很烦的细节就是比较器与输入输出端的下标转换。