HDU 5321 Beautiful Set (莫比乌斯反演 + 逆元 + 组合数学)

题意：给定一个 n 个数的集合，然后让你求两个值，

1。是将这个集合的数进行全排列后的每个区间的gcd之和。

2。是求这个集合的所有的子集的gcd乘以子集大小的和。

析：对于先求出len，len[i]表示能够整除 i 的的个数。

第一个值，根据排列组合，求出gcd是 i 的倍数的个数，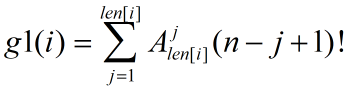

解释一下这个式子，先从len[i]中选出 j 个数，然后进行排列，这就是所选的区间，然后再把这 j 个数看成一个大元素，再和其他的进行排列，也就是(n-j+1)!，总体也就是排列组合。

对于第二个值，

这个式子应该很好理解，就是一个组合问题。

要提前先预处理出来上面那两个式子，处理第一个式子的时候，还要注意处理阶乘的逆元，这个可用费马小定理和快速幂来解决。

处理完上面那个式子后，再用莫比乌斯反演来处理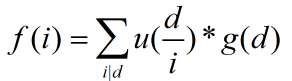，可以得到f1，f2

最后答案就是

代码如下：

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include <cstdio>
#include <string>
#include <cstdlib>
#include <cmath>
#include <iostream>
#include <cstring>
#include <set>
#include <queue>
#include <algorithm>
#include <vector>
#include <map>
#include <cctype>
#include <cmath>
#include <stack>
#include <sstream>
#include <list>
#include <assert.h>
#include <bitset>
#include <numeric>
#define debug() puts("++++")
#define gcd(a, b) __gcd(a, b)
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define fi first
#define se second
#define pb push_back
#define sqr(x) ((x)*(x))
#define ms(a,b) memset(a, b, sizeof a)
#define sz size()
#define pu push_up
#define pd push_down
#define cl clear()
#define lowbit(x) -x&x
//#define all 1,n,1
#define FOR(i,x,n)  for(int i = (x); i < (n); ++i)
#define freopenr freopen("in.txt", "r", stdin)
#define freopenw freopen("out.txt", "w", stdout)
using namespace std;

typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> P;
const int INF = 0x3f3f3f3f;
const LL LNF = 1e17;
const double inf = 1e20;
const double PI = acos(-1.0);
const double eps = 1e-8;
const int maxn = 1e5 + 5;
const int maxm = 2e4 + 10;
const LL mod = 258280327;
const int dr[] = {-1, 1, 0, 0, 1, 1, -1, -1};
const int dc[] = {0, 0, 1, -1, 1, -1, 1, -1};
const char *de[] = {"0000", "0001", "0010", "0011", "0100", "0101", "0110", "0111", "1000", "1001", "1010", "1011", "1100", "1101", "1110", "1111"};
int n, m;
const int mon[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
const int monn[] = {0, 31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
inline bool is_in(int r, int c) {
  return r >= 0 && r < n && c >= 0 && c < m;
}

bool vis[maxn];
int prime[maxn], mu[maxn];

LL fact[maxn], fa[maxn], inv[maxn];

LL fast_pow(LL a, int n){
  LL res = 1;
  while(n){
    if(n&1)  res = res * a % mod;
    a = a * a % mod;
    n >>= 1;
  }
  return res;
}

void Moblus(){
  mu[1] = 1;  int tot = 0;  fa[1] = 2;
  fact[0] = fact[1] = fa[0] = 1;
  for(int i = 2; i < maxn; ++i){
    if(!vis[i])  prime[tot++] = i, mu[i] = -1;
    for(int j = 0; j < tot; ++j){
      int t = i * prime[j];
      if(t >= maxn)  break;
      vis[t] = 1;
      if(i % prime[j] == 0)  break;
      mu[t] = -mu[i];
    }
    fact[i] = (fact[i-1] * i) % mod;
    fa[i] = (fa[i-1]<<1) % mod;
  }
  inv[maxn-1] = fast_pow(fact[maxn-1], mod-2);
  for(int i = maxn-2; i >= 0; --i)
    inv[i] = inv[i+1] * (i+1) % mod;
}

int a[maxn], len[maxn];
LL g1[maxn], g2[maxn];

int main(){
  Moblus();
  while(scanf("%d", &n) == 1){
    ms(len, 0);  ms(a, 0);
    int mmax = 0;
    for(int i = 0; i < n; ++i){
      int x;  scanf("%d", &x);
      ++a[x];  mmax = max(mmax, x);
    }
    for(int i = 1; i <= mmax; ++i)
      for(int j = i; j <= mmax; j += i)
        len[i] += a[j];
    for(int i = 1; i <= mmax; ++i){
      g1[i] = g2[i] = 0;
      if(!len[i])  continue;
      for(int j = 1; j <= len[i]; ++j)
        g1[i] = g1[i] + fact[len[i]] * inv[len[i]-j] % mod * fact[n-j+1] % mod;
      g2[i] = len[i] * fa[len[i]-1] % mod;
    }
    LL ans1 = 0, ans2 = 0;
    for(int i = 1; i <= mmax; ++i){
      LL tmp1 = 0, tmp2 = 0;
      for(int j = i, k = 1; j <= mmax; j += i, ++k){
        tmp1 += mu[k] * g1[j];
        tmp2 += mu[k] * g2[j];
      }
      ans1 = (ans1 + tmp1 * i) % mod;
      ans2 = (ans2 + tmp2 * i) % mod;
    }
    ans1 = (ans1 + mod) % mod;
    ans2 = (ans2 + mod) % mod;
    if(ans1 == ans2)  printf("Equal %lld\n", ans1);
    else if(ans1 > ans2)  printf("Mr. Zstu %lld\n", ans1);
    else  printf("Mr. Hdu %lld\n", ans2);
  }
  return 0;
}