洛谷P1027 Car的旅行路线

洛谷P1027 Car的旅行路线

题目描述

又到暑假了，住在城市A的Car想和朋友一起去城市B旅游。她知道每个城市都有四个飞机场，分别位于一个矩形的四个顶点上，同一个城市中两个机场之间有一条笔直的高速铁路，第I个城市中高速铁路了的单位里程价格为Ti，任意两个不同城市的机场之间均有航线，所有航线单位里程的价格均为t。

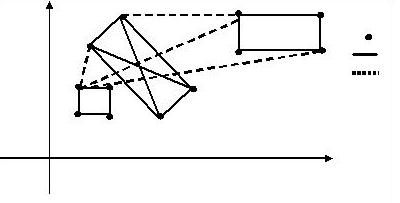
图例（从上而下）

机场 高速铁路

飞机航线

　 注意：图中并没有

标出所有的铁路与航线。

那么Car应如何安排到城市B的路线才能尽可能的节省花费呢?她发现这并不是一个简单的问题，于是她来向你请教。

找出一条从城市A到B的旅游路线，出发和到达城市中的机场可以任意选取，要求总的花费最少。

输入输出格式

输入格式：

第一行为一个正整数n(0<=n<=10)，表示有n组测试数据。

每组的第一行有四个正整数s，t，A，B。

S(0<S<=100)表示城市的个数，t表示飞机单位里程的价格，A，B分别为城市A，B的序号，(1<=A，B<=S)。

接下来有S行，其中第I行均有7个正整数xi1，yi1，xi2，yi2，xi3，yi3，Ti，这当中的(xi1，yi1)，(xi2，yi2)，(xi3，yi3)分别是第I个城市中任意三个机场的坐标，T I为第I个城市高速铁路单位里程的价格。

输出格式：

共有n行，每行一个数据对应测试数据。 保留一位小数

输入输出样例

输入样例#1：

1
3 10 1 3
1 1 1 3 3 1 30
2 5 7 4 5 2 1
8 6 8 8 11 6 3

输出样例#1：

47.5

二、分析

直接算出各个机场之间的费用即可，然后用dijkstra做，这题floyed也可以过。

对于题目每个机场给三个点，我们需要用迭代法不断交换三个点的位置:A-B-C --> B-C-A --> C-A-B使其满足矩形关系。

判断矩形我们可以用垂直关系。

 #include <iostream>
 #include <cstring>
 #include <iomanip>
 #include <cmath>
 #include <algorithm>
 #define INF 10000000
 #define CTOA(x) (((x-1)<<2)+1)
 #define DISTANCE(x1,y1,x2,y2) ((double)sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2))) //自定义宏，开根号操作
 using namespace std;
 double node[][]; //node[i][j]=i点到j点的最短距离
 double T; //t=飞机航线的单价，T=铁路线路的单价
 int tx[],ty[],t;
 double ans=INF;
 struct city
 {
     int x[];
     int y[];
 }ct[]; //ct[i].x[j]=第i个城市第j个机场横坐标，ct[i].y[j]=第i个城市第j个机场纵坐标
 void getfour(int c) //获取第c个城市第四个机场的坐标
 {
     int tt;
     memcpy(tx,ct[c].x,sizeof(tx));
     memcpy(ty,ct[c].y,sizeof(ty));
     while((tx[]-tx[])*(tx[]-tx[])+(ty[]-ty[])*(ty[]-ty[])) //(x1-x2)*(x3-x2)=(y1-y2)*(y3-y2)时，两直线垂直
     {
         tt=tx[]; tx[]=tx[]; tx[]=tx[]; tx[]=tt;
         tt=ty[]; ty[]=ty[]; ty[]=ty[]; ty[]=tt; //点ABC转化为BCA，不断迭代到AB⊥BC
     }
     ct[c].x[]=tx[]-tx[]+tx[];
     ct[c].y[]=ty[]-ty[]+ty[];
 }
 int min(int a1,int b1)
 {
     if(a1<b1) return a1;
     return b1;
 }
 int main()
 {
     int i,j,k,l,m,n;
     scanf("%d",&n);
     while(n--)
     {
         int s,t,a,b;
         cin>>s>>t>>a>>b;
         if(a==b) { cout<<"0.0\n"; continue;} //注意出发点和目的地在同一城市的情况，直接输出0.0
         int airport=s<<; //airport=机场数量
         for(i=;i<=airport;i++)
         {
             for(j=;j<=airport;j++)
                 node[i][j]=INF; //初始化各点间的路的距离为无穷大
         }
         for(i=;i<=s;i++)
         {
             for(j=;j<;j++)
                 cin>>ct[i].x[j]>>ct[i].y[j];
             cin>>T;
             getfour(i); //将第i个城市第四个机场确定
             for(j=;j<;j++)
             {
                 for(k=;k<;k++)
                     if(j!=k) //不是同一个机场的话，勾股定理初始化二者间的花费（花费=距离*每单位路程单价）
                         node[CTOA(i)+j][CTOA(i)+k]=(DISTANCE(ct[i].x[j],ct[i].y[j],ct[i].x[k],ct[i].y[k])*T);
             }
         }
         for(i=;i<=s;i++)
         {
             for(j=;j<=s;j++)
             {
                 if(i!=j) //如果i、j不是同一个城市
                     for(k=;k<;k++) //第i个城市的第k个机场
                     {
                         for(l=;l<;l++) //第j个城市的第l个机场
                             node[CTOA(i)+k][CTOA(j)+l]=(DISTANCE(ct[i].x[k],ct[i].y[k],ct[j].x[l],ct[j].y[l])*t);
                     }
             }
         }
         //Floyd
         for(k=;k<=airport;k++)
         {
             for(i=;i<=airport;i++)
             {
                 for(j=;j<=airport;j++)
                 {
                     node[i][j]=min(node[i][j],node[i][k]+node[k][j]);
                 }
             }
         }
         for(i=;i<;i++)
         {
             for(j=;j<;j++)
                 ans=min(ans,node[CTOA(a)+i][CTOA(b)+j]);
         }
         cout<<setiosflags(ios::fixed)<<setprecision()<<ans<<endl;
     }
     return ;
 }