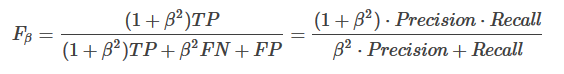机器学习性能指标精确率、召回率、F1值、ROC、PRC与AUC--周振洋
机器学习性能指标精确率、召回率、F1值、ROC、PRC与AUC
精确率、召回率、F1、AUC和ROC曲线都是评价模型好坏的指标,那么它们之间有什么不同,又有什么联系呢。下面让我们分别来看一下这几个指标分别是什么意思。
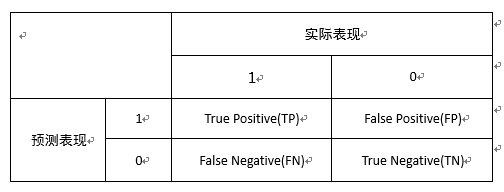
针对一个二分类问题,将实例分成正类(postive)或者负类(negative)。但是实际中分类时,会出现四种情况.
(1)若一个实例是正类并且被预测为正类,即为真正类(True Postive TP)
(2)若一个实例是正类,但是被预测成为负类,即为假负类(False Negative FN)
(3)若一个实例是负类,但是被预测成为正类,即为假正类(False Postive FP)
(4)若一个实例是负类,但是被预测成为负类,即为真负类(True Negative TN)
如下图所示:
精确率(Precision)为TP/(TP+FP),即实际是正类并且被预测为正类的样本占所有预测为正类的比例,精确率更为关注将负样本错分为正样本(FP)的情况。
召回率(Recall)为TP/(TP+FN),即实际是正类并且被预测为正类的样本占所有实际为正类样本的比例,召回率更为关注将正样本分类为负样本(FN)的情况。
F1值是精确率和召回率的调和均值,即F1=2PR/(P+R) (P代表精确率,R代表召回率),相当于精确率和召回率的综合评价指标。
有的时候,我们对recall 与 precision 赋予不同的权重,表示对分类模型的偏好:
可以看到,当 ,那么就退回到了, 其实反映了模型分类能力的偏好, 的时候,precision的权重更大,为了提高,我们希望precision 越小,而recall 应该越大,说明模型更偏好于提升recall,意味着模型更看重对正样本的识别能力; 而 的时候,recall 的权重更大,因此,我们希望recall越小,而precision越大,模型更偏好于提升precision,意味着模型更看重对负样本的区分能力。
ROC曲线其实是多个混淆矩阵的结果组合,如果在上述模型中我们没有定好阈值,而是将模型预测结果从高到低排序,将每个概率值依次作为阈值,那么就有多个混淆矩阵。
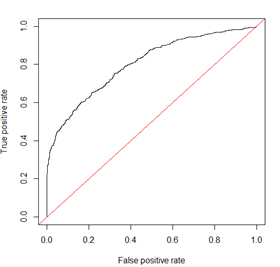
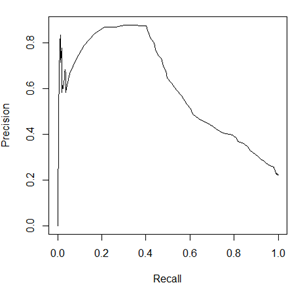
除此之外,在评价模型时还会用到KS(Kolmogorov-Smirnov)值,KS=max(TPR-FPR),即为TPR与FPR的差的最大值,KS值可以反映模型的最优区分效果,此时所取的阈值一般作为定义好坏用户的最优阈值。
相对来讲ROC曲线会稳定很多,在正负样本量都足够的情况下,ROC曲线足够反映模型的判断能力。
因此,对于同一模型,PRC和ROC曲线都可以说明一定的问题,而且二者有一定的相关性,如果想评测模型效果,也可以把两条曲线都画出来综合评价。
对于有监督的二分类问题,在正负样本都足够的情况下,可以直接用ROC曲线、AUC、KS评价模型效果。在确定阈值过程中,可以根据Precision、Recall或者F1来评价模型的分类效果。
对于多分类问题,可以对每一类分别计算Precision、Recall和F1,综合作为模型评价指标。
机器学习性能指标精确率、召回率、F1值、ROC、PRC与AUC--周振洋的更多相关文章
- 混淆矩阵、准确率、精确率/查准率、召回率/查全率、F1值、ROC曲线的AUC值
准确率.精确率(查准率).召回率(查全率).F1值.ROC曲线的AUC值,都可以作为评价一个机器学习模型好坏的指标(evaluation metrics),而这些评价指标直接或间接都与混淆矩阵有关,前 ...
- LightGBM详细用法--机器学习算法--周振洋
LightGBM算法总结 2018年08月21日 18:39:47 Ghost_Hzp 阅读数:2360 版权声明:本文为博主原创文章,未经博主允许不得转载. https://blog.csdn.ne ...
- 机器学习sklearn的快速使用--周振洋
ML神器:sklearn的快速使用 传统的机器学习任务从开始到建模的一般流程是:获取数据 -> 数据预处理 -> 训练建模 -> 模型评估 -> 预测,分类.本文我们将依据传统 ...
- XGBoost——机器学习--周振洋
XGBoost——机器学习(理论+图解+安装方法+python代码) 目录 一.集成算法思想 二.XGBoost基本思想 三.MacOS安装XGBoost 四.用python实现XGBoost算法 在 ...
- LightGBM的并行优化--机器学习-周振洋
LightGBM的并行优化 上一篇文章介绍了LightGBM算法的特点,总结起来LightGBM采用Histogram算法进行特征选择以及采用Leaf-wise的决策树生长策略,使其在一批以树模型为基 ...
- 准确率、精确率、召回率、F1
在搭建一个AI模型或者是机器学习模型的时候怎么去评估模型,比如我们前期讲的利用朴素贝叶斯算法做的垃圾邮件分类算法,我们如何取评估它.我们需要一套完整的评估方法对我们的模型进行正确的评估,如果模型效果比 ...
- [机器学习] 性能评估指标(精确率、召回率、ROC、AUC)
混淆矩阵 介绍这些概念之前先来介绍一个概念:混淆矩阵(confusion matrix).对于 k 元分类,其实它就是一个k x k的表格,用来记录分类器的预测结果.对于常见的二元分类,它的混淆矩阵是 ...
- 准确率(Accuracy), 精确率(Precision), 召回率(Recall)和F1-Measure(对于二分类问题)
首先我们可以计算准确率(accuracy),其定义是: 对于给定的测试数据集,分类器正确分类的样本数与总样本数之比.也就是损失函数是0-1损失时测试数据集上的准确率. 下面在介绍时使用一下例子: 一个 ...
- Recall(召回率)and Precision(精确率)
◆版权声明:本文出自胖喵~的博客,转载必须注明出处. 转载请注明出处:http://www.cnblogs.com/by-dream/p/7668501.html 前言 机器学习中经过听到" ...
随机推荐
- 第13章 GPIO输入—按键检测
本章参考资料:<STM32F76xxx参考手册>.库帮助文档<STM32F779xx_User_Manual.chm>. 按键检测使用到GPIO外设的基本输入功能,本章中不再赘 ...
- AngularJS 四 服务
AngularJS服务: API: https://docs.angularjs.org/api/ng/service 下面只会介绍几种,需要的话可以去官网查看 AngularJS服务 ...
- 【2017 World Final E】Need For Speed(二分)
Sheila is a student and she drives a typical student car: it is old, slow, rusty, and falling apart. ...
- ABAP术语-ALE
ALE 原文:http://www.cnblogs.com/qiangsheng/archive/2007/12/13/993351.html Application Link Enabling (A ...
- Windows下远程桌面的连接
[系统环境] 建议Windows7以上 [步骤说明] 1.使用"WIN + R"组合键打开"运行"对话框,然后输入“mstsc”,点击确定,如下图所示: 2.点 ...
- ArrayList调用remove(int index)抛出UnsupportedOperationException问题分析以及解决记录
使用Arrays转数组成为List后,不能调用add(...)和remove(...)方法,此时如果调用就会抛出UnsupportedOperationException异常 原因 其实Arrays. ...
- TCP/IP协议模型详解
TCP
- mysql 使用 FIND_IN_SET 来查询数据
mysql中find_in_set函数很有意思,它的功能是查找以英文逗号隔开的值,我们可以将数据存储类似为1,2,3,4格式.今天我们就来看看在thinkphp中怎样正确地使用find_in_set函 ...
- .NET中获取当前的IP地址
/// <summary> /// 获取本地IP地址信息 /// </summary> public static string GetAddressIP() { ///获取本 ...
- 在Liunx上搭建FTP并配置用户权限
伴随着.Net Core的开源,公司前几天上了新的Liunx服务器,我在前几篇文章中介绍了如何搭建环境以及部署.Net Core应用. 然后,今天客户和我说想自己给网站做推广,需要用FTP链接我们的服 ...