[C++] 贪心算法之活动安排、背包问题

一、贪心算法的基本思想

　　在求解过程中，依据某种贪心标准，从问题的初始状态出发，直接去求每一步的最优解，通过若干次的贪心选择，最终得出整个问题的最优解。

　　从贪心算法的定义可以看出，贪心算法不是从整体上考虑问题，它所做出的选择只是在某种意义上的局部最优解，而由问题自身的特性决定了该题运用贪心算法可以得到最优解。如果一个问题可以同时用几种方法解决，贪心算法应该是最好的选择之一。

二、贪心算法的基本要素

　　（1）最优子结构性质

　　（2）贪心选择性质（局部最优选择）

三、贪心算法实例

　　1、活动安排

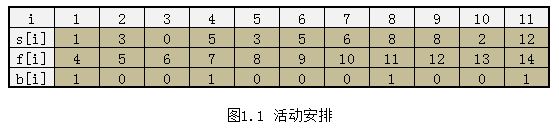
　　设有n个活动的集合 E ＝ {1,2,…,n}，其中每个活动都要求使用同一资源，如演讲会场等，而在同一时间内只有一个活动能使用这一资源。

　　每个活动 i 都有一个要求使用该资源的起始时间 s_i 和一个结束时间 f_i，且 s_i ＜ f_i。如果选择了活动i，则它在半开时间区间 [s_i ,f_i ) 内占用资源。若区间 [s_i , f_i )与区间 [s_j, f_j ) 不相交，则称活动i与活动j是相容的。当 s_i ≥ f_j 或 s_j ≥ f_i 时，活动 i 与活动 j 相容。

　　活动安排问题就是在所给的活动集合中选出最大的相容活动子集合。

　　例如：

 #include <iostream>
 using namespace std;   

 #define NUM 50 

 void GreedySelector(int n, int s[], int f[], bool b[])
 {
     b[]=true;  //默认将第一个活动先安排
     int j=;    //记录最近一次加入b中的活动  

       //依次检查活动i是否与当前已选择的活动相容
     for(int i=;i<=n;i++)
     {
         if (s[i]>=f[j])
         {
             b[i]=true;
             j=i;
         }
         else
             b[i]=false;
     }
 }

 int main()
 {
     int s[] = {,,,,,,,,,,,};          //存储活动开始时间
     int f[] = {,,,,,,,,,,,};      //存储活动结束时间
     bool b[NUM];  //存储被安排的活动编号
      int n = (sizeof(s) / sizeof(s[])) - ;

     GreedySelector(n, s, f, b);

     for(int i = ; i <= n; i++)      //输出被安排的活动编号和它的开始时间和结束时间
     {
         if(b[i]) cout << "活动 " << i << " :" << "(" << s[i] << "," << f[i] << ")" <<endl;
     }
     return ;
 }  

　　2、背包问题

　　给定一个载重量为 M 的背包，考虑 n 个物品，其中第 i 个物品的重量 w_i（1 ≤ i ≤ n），价值 v_i（1 ≤ i ≤ n），要求把物品装满背包，且使背包内的物品价值最大。
　　有两类背包问题（根据物品是否可以分割），如果物品不可以分割，称为 0—1 背包问题（动态规划）；如果物品可以分割，则称为背包问题（贪心算法）。

　　例如：

　　有3种方法来选取物品：

　　　　（1）当作 0—1 背包问题，用动态规划算法，获得最优值 220；
　　　　（2）当作 0—1 背包问题，用贪心算法，按性价比从高到底顺序选取物品，获得最优值 160。由于物品不可分割，剩下的空间白白浪费。
　　　　（3）当作背包问题，用贪心算法，按性价比从高到底的顺序选取物品，获得最优值 240。由于物品可以分割，剩下的空间装入物品 3 的一部分，而获得了更好的性能。

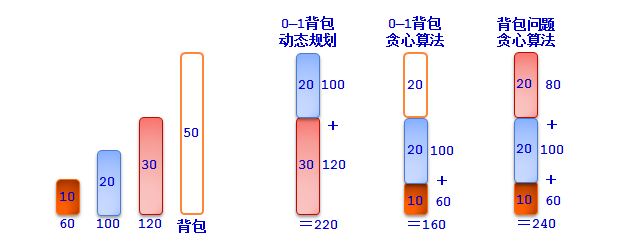
图2.1 背包问题

 #include <iostream>
 using namespace std;   

 #define NUM 50

 //这里假设 w[], v[] 已按要求排好序
 void Knapsack(int n,float M,float v[],float w[],float x[])
 {
     int i;
     for(i = ; i <= n; i++) x[i] = ;    //初始化数组
     float c  =  M;
     for(i = ;i <= n; i++)                //全部被装下的物品,且将 x[i] = 1
     {
         if(w[i]>c) break;
         x[i] = ;
         c -= w[i];
     }  

     if(i <= n) x[i] = c / w[i];  //将物品i 的部分装下
 } 

 int main()
 {
     float M = ;                //背包所能容纳的重量
     float w[] = {,,,};   //这里给定的物品按价值降序排序
     float v[] = {,,,};
       float x[NUM];                //存储每个物品装入背包的比例 

     int n = (sizeof(w) / sizeof(w[])) - ; 

     Knapsack(n, M, v, w, x);

     for(int i = ; i <= n; i++)
         cout << "物品 " << i << " 装入的比例: " << x[i] << endl;
     return ;
 }