hdu-2582 f(n)---找规律+素数筛法

题目链接：

http://acm.hdu.edu.cn/showproblem.php?pid=2582

题目大意：

给出公式Gcd(n)=gcd(C[n][1],C[n][2],……,C[n][n-1])，让求f(n)= Gcd(3)+Gcd(4)+…+Gcd(i)+…+Gcd(n)。

解题思路：

对于公式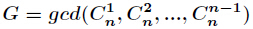：，小范围打表可以找出规律：

(1)，如果n为素数，那么G=n；
(2)，如果n有多个素因子，那么G=1；
(3)，如果n只有一个素因子，那么G=该素因子。

所以可以直接利用筛素数的模板，筛出一个素数时就往后更新答案即可

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 const int maxn = +;
 ll ans[maxn];
 bool is_prime[maxn];
 int sieve(int n)//返回n以内素数的个数
 {
     int p = ;
     for(int i = ; i <= n; i++)is_prime[i] = ans[i] = ;
     is_prime[] = is_prime[] = ;
     for(ll i = ; i <= n; i++)
     {
         if(is_prime[i])
         {
             ans[i] = i;
             for(ll j = i * ; j <= n; j += i)is_prime[j] = ;
             for(ll j = i * i; j <= n; j *= i)ans[j] = i;
         }
     }
     for(int i = ; i <= n; i++)ans[i] += ans[i - ];
     return p;
 }
 int main()
 {
     int tot = sieve(), n;
     while(scanf("%d", &n) != EOF)
         printf("%lld\n", ans[n]);
     return ;
 }