Unity3D 向量运算

写在前面的话，前两天有个朋友在QQ上问我 如何获取主角面朝方向一定区域中的敌人对象。这个命题看似简单，其实里面蕴含了很多数学方面的东西。今天刚好有时间我就彻底的把这个疑问写在博客中。希望可以帮助到他。

在上代码之前请大家跟我先做几个简单的练习题，角度向量的计算一定要学会，不然后面的东西会很难懂。

1.已知3D坐标，和一个旋转角度，以及一段距离，求目标点的3D坐标。

已知当前点为Target，目标点沿着Target的Y轴旋转30度，沿着Target的X轴延伸10米求目标点的3D坐标？

using System.Collections;

public class Test : MonoBehaviour
{

	public Transform Target;

	void LateUpdate ()
	{
		Quaternion rotation = Quaternion.Euler(0f,30f,0f) * Target.rotation;
		Vector3  newPos = rotation * new Vector3(10f,0f,0f);
		Debug.DrawLine(newPos,Vector3.zero,Color.red);
		Debug.Log("newpos " + newPos +" nowpos " + Target.position + " distance " + Vector3.Distance(newPos,Target.position));
	}

}

输出结果 ：新坐标 (8.7, 0.0, -5.0) 当前坐标 (0.0, 0.0, 0.0)两点之间的距离 10。

 2.已知3D模型的角度求它的向量。

已知3D模型Target，Y轴旋转30度后向前平移。

using UnityEngine;
using System.Collections;

public class Test : MonoBehaviour
{

	public Transform Target;

	void LateUpdate ()
	{

		if(Input.GetMouseButton(0))
		{
			Quaternion rotation = Quaternion.Euler(0f,30f,0f) * Target.rotation;
			Vector3  newPos = rotation * Vector3.forward;
			Target.Translate(newPos.x,newPos.y,newPos.z);
		}
	}

}

3.已知一个目标点，让模型朝着这个目标点移动。

Target.transform.LookAt(new Vector3 (100f,200f,300f));
			Target.Translate(Vector3.forward);

 这里我要说的就是Vector3.forward ，它等价与 new Vector3(0,0,1)；它并不是一个坐标，它是一个标准向量，方向是沿着Z轴向前。这样平移一次的距离就是1米， 如果Vector3.forward * 100那么一次平移的距离就是100米。 

 在看看下面这段代码

 这是一个比较简单的例子，大家应该都能看明白。

Vector3 vecn = (TargetCube.position - Target.position).normalized;
Target.Translate(vecn *0.1f);

用向量减去一个向量求出它们的差值，normalized 是格式化向量，意思是把它们之间向量格式化到1米内。这样就可以更加精确的计算一次平移的距离了 vecn *0.1f 就标示一次平移1分米，蛤蛤。

 向量不仅可以进行X Y Z轴的移动，同样可以进行旋转 ，下面这段代码就是让向量沿着Y轴旋转30度。

Vector3 vecn = (TargetCube.position - Target.position).normalized;
vecn = Quaternion.Euler(0f,30f,0f) * vecn;
Target.Translate(vecn *0.1f);

如果上述三道简单的练习题 你都能了然于心的话，那么本文最大的难题我相信也不会是什么难事，继续阅读吧。

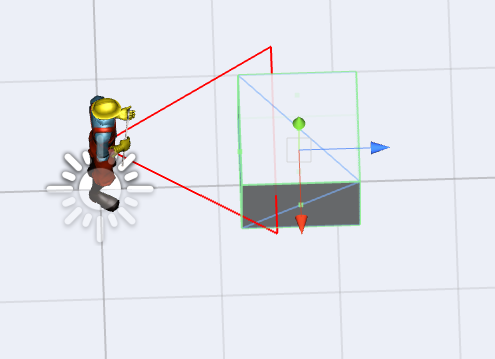
假设我们需要计算主角面前5米内所有的对象时。以主角为圆心计算面前5米外的一个点，为了让大家看清楚我现将这条线绘制出来。

private float distance = 5f;
void Update ()
{
	Quaternion r= transform.rotation;
	Vector3 f0 =  (transform.position  + (r *Vector3.forward) * distance);
	Debug.DrawLine(transform.position,f0,Color.red);
}

如下图所，我们已经将这两个点计算出来了。此时你可以动态的编辑主角Y轴的坐标，这个点永远都是沿着主角当前角度面前5米以外的点。

接下来，我们需要计算主角面前的一个发散性的角度。假设主角看到的是向左30度，向右30度在这个区域。

void Update ()
{
	Quaternion r= transform.rotation;
	Vector3 f0 =  (transform.position  + (r *Vector3.forward) * distance);
	Debug.DrawLine(transform.position,f0,Color.red);

	Quaternion r0= Quaternion.Euler(transform.rotation.eulerAngles.x,transform.rotation.eulerAngles.y - 30f,transform.rotation.eulerAngles.z);
	Quaternion r1= Quaternion.Euler(transform.rotation.eulerAngles.x,transform.rotation.eulerAngles.y + 30f,transform.rotation.eulerAngles.z);

	Vector3 f1 =  (transform.position  + (r0 *Vector3.forward) * distance);
	Vector3 f2 =  (transform.position  + (r1 *Vector3.forward) * distance);

	Debug.DrawLine(transform.position,f1,Color.red);
	Debug.DrawLine(transform.position,f2,Color.red);

	Debug.DrawLine(f0,f1,Color.red);
	Debug.DrawLine
}

如下图所示，这时主角面前的区域就计算出来了。看起来就是两个三角形之间的区域。

最后就是简单的套用公式，计算一个点是否在三角形内，在本文中就是计算敌人的点是否在面前的这两个三角形内。

using System.Collections;

public class MyTest : MonoBehaviour {

	public Transform cube;

	private float distance = 5f;
	void Update ()
	{
		Quaternion r= transform.rotation;
		Vector3 f0 =  (transform.position  + (r *Vector3.forward) * distance);
		Debug.DrawLine(transform.position,f0,Color.red);

		Quaternion r0= Quaternion.Euler(transform.rotation.eulerAngles.x,transform.rotation.eulerAngles.y - 30f,transform.rotation.eulerAngles.z);
		Quaternion r1= Quaternion.Euler(transform.rotation.eulerAngles.x,transform.rotation.eulerAngles.y + 30f,transform.rotation.eulerAngles.z);

		Vector3 f1 =  (transform.position  + (r0 *Vector3.forward) * distance);
		Vector3 f2 =  (transform.position  + (r1 *Vector3.forward) * distance);

		Debug.DrawLine(transform.position,f1,Color.red);
		Debug.DrawLine(transform.position,f2,Color.red);

		Debug.DrawLine(f0,f1,Color.red);
		Debug.DrawLine(f0,f2,Color.red);

		Vector3 point = cube.position;

		if(isINTriangle(point,transform.position,f1,f0) || isINTriangle(point,transform.position,f2,f0) )
		{
			Debug.Log("cube in this !!!");
		}else
		{
			Debug.Log("cube not in this !!!");
		}

	}

	private  float triangleArea(float v0x,float v0y,float v1x,float v1y,float v2x,float v2y)
	{
        return Mathf.Abs((v0x * v1y + v1x * v2y + v2x * v0y
            - v1x * v0y - v2x * v1y - v0x * v2y) / 2f);
    }

	bool isINTriangle(Vector3 point,Vector3 v0,Vector3 v1,Vector3 v2)
	{
		float x = point.x;
		float y = point.z;

		float v0x = v0.x;
		float v0y = v0.z;

		float v1x = v1.x;
		float v1y = v1.z;

		float v2x = v2.x;
		float v2y = v2.z;

		float t = triangleArea(v0x,v0y,v1x,v1y,v2x,v2y);
		float a = triangleArea(v0x,v0y,v1x,v1y,x,y) + triangleArea(v0x,v0y,x,y,v2x,v2y) + triangleArea(x,y,v1x,v1y,v2x,v2y);

		if (Mathf.Abs(t - a) <= 0.01f)
		{
			return true;
		}else
		{
			return false;
		}
	}
}

如下图所示，如果箱子对象是主角的视野中就会检测到。

注意，上图中我的视野选择了两个三角形，如果你需要视野目标点是椭圆形的话，那么可以多设置一些三角形。但是这样就会非常消耗效率，我觉得这里完全可以使用1个三角形，，只是正对的目标点会出现一些偏差，影响其实并不会很大。如下图所示

代码简单的修改一下即可。

public class MyTest : MonoBehaviour {

	public Transform cube;

	private float distance = 5f;
	void Update ()
	{
		Quaternion r= transform.rotation;
		Vector3 f0 =  (transform.position  + (r *Vector3.forward) * distance);
		Debug.DrawLine(transform.position,f0,Color.red);

		Quaternion r0= Quaternion.Euler(transform.rotation.eulerAngles.x,transform.rotation.eulerAngles.y - 30f,transform.rotation.eulerAngles.z);
		Quaternion r1= Quaternion.Euler(transform.rotation.eulerAngles.x,transform.rotation.eulerAngles.y + 30f,transform.rotation.eulerAngles.z);

		Vector3 f1 =  (transform.position  + (r0 *Vector3.forward) * distance);
		Vector3 f2 =  (transform.position  + (r1 *Vector3.forward) * distance);

		Debug.DrawLine(transform.position,f1,Color.red);
		Debug.DrawLine(transform.position,f2,Color.red);
		Debug.DrawLine(f1,f2,Color.red);

		Vector3 point = cube.position;

		if(isINTriangle(point,transform.position,f1,f2))
		{
			Debug.Log("cube in this !!!");
		}else
		{
			Debug.Log("cube not in this !!!");
		}

	}

	private  float triangleArea(float v0x,float v0y,float v1x,float v1y,float v2x,float v2y)
	{
        return Mathf.Abs((v0x * v1y + v1x * v2y + v2x * v0y
            - v1x * v0y - v2x * v1y - v0x * v2y) / 2f);
    }

	bool isINTriangle(Vector3 point,Vector3 v0,Vector3 v1,Vector3 v2)
	{
		float x = point.x;
		float y = point.z;

		float v0x = v0.x;
		float v0y = v0.z;

		float v1x = v1.x;
		float v1y = v1.z;

		float v2x = v2.x;
		float v2y = v2.z;

		float t = triangleArea(v0x,v0y,v1x,v1y,v2x,v2y);
		float a = triangleArea(v0x,v0y,v1x,v1y,x,y) + triangleArea(v0x,v0y,x,y,v2x,v2y) + triangleArea(x,y,v1x,v1y,v2x,v2y);

		if (Mathf.Abs(t - a) <= 0.01f)
		{
			return true;
		}else
		{
			return false;
		}
	}
}

上面我们介绍了三角形判断，当然也可以通过矩形来判断是否相交。。

public class MyTest : MonoBehaviour {

	public Transform cube;

	private float distance = 5f;
	void Update ()
	{
		Quaternion r= transform.rotation;
		Vector3 left =  (transform.position  + (r *Vector3.left) * distance);
		Debug.DrawLine(transform.position,left,Color.red);

		Vector3 right =  (transform.position  + (r *Vector3.right) * distance);
		Debug.DrawLine(transform.position,right,Color.red);

		Vector3 leftEnd = (left  + (r *Vector3.forward) * distance);
		Debug.DrawLine(left,leftEnd,Color.red);

		Vector3 rightEnd = (right  + (r *Vector3.forward) * distance);
		Debug.DrawLine(right,rightEnd,Color.red);

		Debug.DrawLine(leftEnd,rightEnd,Color.red);

		Vector3 point = cube.position;

		if(isINRect(point,leftEnd,rightEnd,right,left))
		{
			Debug.Log("cube in this !!!");
		}else
		{
			Debug.Log("cube not in this !!!");
		}

	}

     private float Multiply(float p1x , float p1y, float p2x,float p2y, float p0x,float p0y)
     {
        return ((p1x - p0x) * (p2y - p0y) - (p2x - p0x) * (p1y - p0y));
     }

	bool isINRect(Vector3 point,Vector3 v0,Vector3 v1,Vector3 v2,Vector3 v3)
	{
		float x = point.x;
		float y = point.z;

		float v0x = v0.x;
		float v0y = v0.z;

		float v1x = v1.x;
		float v1y = v1.z;

		float v2x = v2.x;
		float v2y = v2.z;

		float v3x = v3.x;
		float v3y = v3.z;

		if (Multiply(x,y, v0x,v0y, v1x,v1y) * Multiply(x,y, v3x,v3y, v2x,v2y) <= 0 && Multiply(x,y, v3x,v3y, v0x,v0y) * Multiply(x,y, v2x,v2y, v1x,v1y) <= 0)
             return true;
		else
            return false;

	}

}

这里我以角色左右个30度。 这样就可以根据两个模型的距离以及角度来判断了。。

public class NewBehaviourScript : MonoBehaviour {

	public Transform target;

	void Update()
	{

			float distance = Vector3.Distance(target.position,transform.position);

			Quaternion right	 = transform.rotation * Quaternion.AngleAxis(30,Vector3.up);
			Quaternion left	 = transform.rotation * Quaternion.AngleAxis(30,Vector3.down);

			Vector3 n = 	transform.position + (Vector3.forward * distance);
			Vector3 leftPoint = left * 	n ;
			Vector3 rightPoint =  right *n ;

			Debug.DrawLine(transform.position,leftPoint,Color.red);
			Debug.DrawLine(transform.position,rightPoint,Color.red);
			Debug.DrawLine(rightPoint,leftPoint,Color.red);

	}
}

文章地址：http://www.xuanyusong.com/archives/1977