NYOJ 163 Phone List （字符串处理 字典树）

题目链接

描述

Given a list of phone numbers, determine if it is consistent in the sense that no number is the prefix of another. Let's say the phone catalogue listed these numbers:

Emergency 911

Alice 97 625 999

Bob 91 12 54 26

In this case, it's not possible to call Bob, because the central would direct your call to the emergency line as soon as you had dialled the first three digits of Bob's phone number. So this list would not be consistent.

输入

The first line of input gives a single integer, 1 ≤ t ≤ 10, the number of test cases. Each test case starts with n, the number of phone numbers, on a separate line, 1 ≤ n ≤ 100000. Then follows n lines with one unique phone number on each line. A phone number is a sequence of at most ten digits.

输出

For each test case, output "YES" if the list is consistent, or "NO" otherwise.

样例输入

2

3

911

97625999

91125426

5

113

12340

123440

12345

98346

样例输出

NO

YES

分析：

其实题目的意思是很简单的，就是在给出的n个电话号码中，找出是否有那个电话号码（必须是这个整体的电话号码，而不是它的一部分）是另一个电话号码的前缀。

这道题是一道典型的字典树的应用，下面补充一下字典树的知识。

1. Trie树

Trie树，即字典树，又称单词查找树或键树，是一种树形结构，是一种哈希树的变种。典型应用是用于统计和排序大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的优点是：最大限度地减少无谓的字符串比较，查询效率比哈希表高。

Trie的核心思想是空间换时间。利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。

它有3个基本性质：

1. 根节点不包含字符，除根节点外每一个节点都只包含一个字符。

2. 从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串。

3. 每个节点的所有子节点包含的字符都不相同。

4. 字典树的构建

题目：给你100000个长度不超过10的单词。对于每一个单词，我们要判断他出没出现过，如果出现了，求第一次出现在第几个位置。

分析：这题当然可以用hash来解决，但是本文重点介绍的是trie树，因为在某些方面它的用途更大。比如说对于某一个单词，我们要询问它的前缀是否出现过。这样hash就不好搞了，而用trie还是很简单。

假设我要查询的单词是abcd，那么在他前面的单词中，以b，c，d，f之类开头的我显然不必考虑。而只要找以a开头的中是否存在abcd就可以了。同样的，在以a开头中的单词中，我们只要考虑以b作为第二个字母的，一次次缩小范围和提高针对性，这样一个树的模型就渐渐清晰了。

好比假设有b，abc，abd，bcd，abcd，efg，hii 这6个单词，我们构建的树就是如下图这样的：

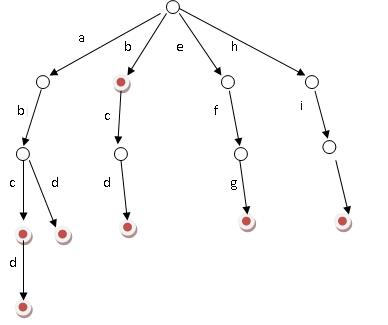
ok，如上图所示，对于每一个节点，从根遍历到他的过程就是一个单词，如果这个节点被标记为红色，就表示这个单词存在，否则不存在。

那么，对于一个单词，我只要顺着他从根走到对应的节点，再看这个节点是否被标记为红色就可以知道它是否出现过了。把这个节点标记为红色，就相当于插入了这个单词。

这样一来我们查询和插入可以一起完成（重点体会这个查询和插入是如何一起完成的，稍后，下文具体解释），所用时间仅仅为单词长度，在这一个样例，便是10。

我们可以看到，trie树每一层的节点数是26^i级别的。所以为了节省空间。我们用动态链表，或者用数组来模拟动态。空间的花费，不会超过单词数×单词长度。

已知n个由小写字母构成的平均长度为10的单词,判断其中是否存在某个串为另一个串的前缀子串。下面对比3种方法：

1.最容易想到的：即从字符串集中从头往后搜，看每个字符串是否为字符串集中某个字符串的前缀，复杂度为O(n^2)。

2.使用hash：我们用hash存下所有字符串的所有的前缀子串，建立存有子串hash的复杂度为O(nlen)，而查询的复杂度为O(n) O(1)= O(n)。

3.使用trie：因为当查询如字符串abc是否为某个字符串的前缀时，显然以b,c,d....等不是以a开头的字符串就不用查找了。所以建立trie的复杂度为O(nlen)，而建立+查询在trie中是可以同时执行的，建立的过程也就可以成为查询的过程，hash就不能实现这个功能。所以总的复杂度为O(nlen)，实际查询的复杂度也只是O(len)。（说白了，就是Trie树的平均高度h为len，所以Trie树的查询复杂度为O（h）=O（len）。好比一棵二叉平衡树的高度为logN，则其查询，插入的平均时间复杂度亦为O（logN））。

1. 查询

Trie树是简单但实用的数据结构，通常用于实现字典查询。我们做即时响应用户输入的AJAX搜索框时，就是Trie开始。本质上，Trie是一颗存储多个字符串的树。相邻节点间的边代表一个字符，这样树的每条分支代表一则子串，而树的叶节点则代表完整的字符串。和普通树不同的地方是，相同的字符串前缀共享同一条分支。下面，再举一个例子。给出一组单词，inn, int, at, age, adv, ant, 我们可以得到下面的Trie：

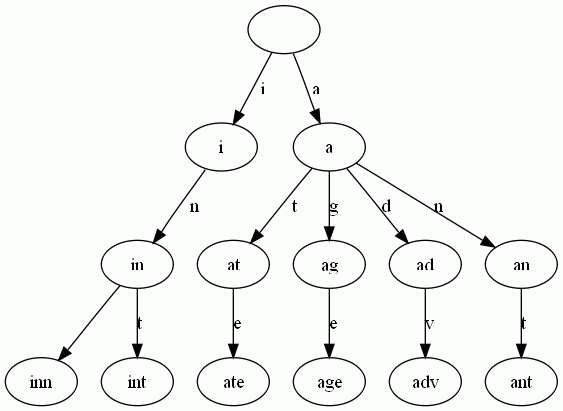
可以看出：

• 每条边对应一个字母。
• 每个节点对应一项前缀。叶节点对应最长前缀，即单词本身。
• 单词inn与单词int有共同的前缀“in”, 因此他们共享左边的一条分支，root->i->in。同理，ate, age, adv, 和ant共享前缀"a"，所以他们共享从根节点到节点"a"的边。

查询操纵非常简单。比如要查找int，顺着路径i -> in -> int就找到了。

搭建Trie的基本算法也很简单，无非是逐一把每则单词的每个字母插入Trie。插入前先看前缀是否存在。如果存在，就共享，否则创建对应的节点和边。比如要插入单词add，就有下面几步：

1. 考察前缀"a"，发现边a已经存在。于是顺着边a走到节点a。
2. 考察剩下的字符串"dd"的前缀"d"，发现从节点a出发，已经有边d存在。于是顺着边d走到节点ad
3. 考察最后一个字符"d"，这下从节点ad出发没有边d了，于是创建节点ad的子节点add，并把边ad->add标记为d。

代码：

#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
struct Node
{
    Node *next[10];///因为电话号码只涉及0~9这是个数字，数组开10就够了
    int end;
    Node()
    {
        memset(next,NULL,sizeof(next));
        end=0;
    }
};
Node *root;
int Insert(char *ch)
{
    Node *now=root;
    int op,flag=0;
    for(int i=0; ch[i]!='\0'; i++)
    {
        op=ch[i]-'0';
        if(now->next[op]==NULL)///当前这个根下没有这个子节点
        {
            now->next[op]=new Node();///构建这个子节点
            flag=1;///标记添加过节点
        }
        now=now->next[op];///指向子节点
        if(now->end==1)///如果已经指向最后了，也就意味着有一个号码是当前这个号码的前缀
            return 0;
    }
    now->end=1;///当前这个号码输入结束
    if(flag==0) return 0;///没有加入节点，一就意味着当前的这个号码是其余电话号码的前缀
    return 1;///没有前缀
}

void clean(Node *now)///把这个树释放
{
    if(now==NULL) return ;
    for(int i=0; i<10; i++)
        if(now->next[i])
            clean(now->next[i]);
    delete now;
}
int main()
{
    int T,n,flag;

    char ch[15];
    scanf("%d",&T);
    while(T--)
    {
        root=new Node();
        flag=true;
        scanf("%d",&n);
        while(n--)
        {
            scanf(" %s",ch);
            if(flag==1)
                flag=Insert(ch);
        }
        clean(root);
        if(flag) printf("YES\n");
        else
            printf("NO\n");
    }
    return 0;
}