《用 Python 学微积分》笔记 1

《用 Python 学微积分》原文见参考资料 1。

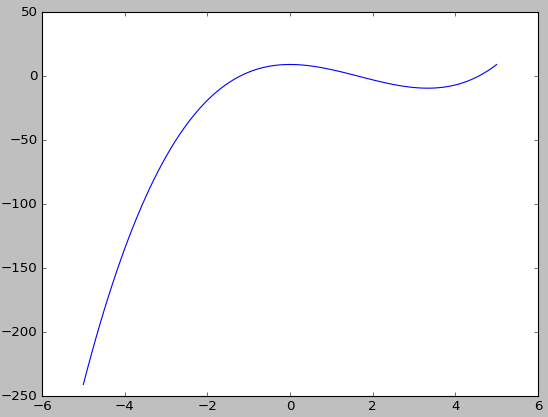
1、多项式

f(x)=x³-5x²+9

def f(x):
    return x**3 - 5*x**2 + 9

print f(3)
print f(1)

import numpy as np
x = np.linspace(-5, 5, num = 100)
y = f(x)
import matplotlib.pyplot as plt
plt.plot(x,y)
plt.show()

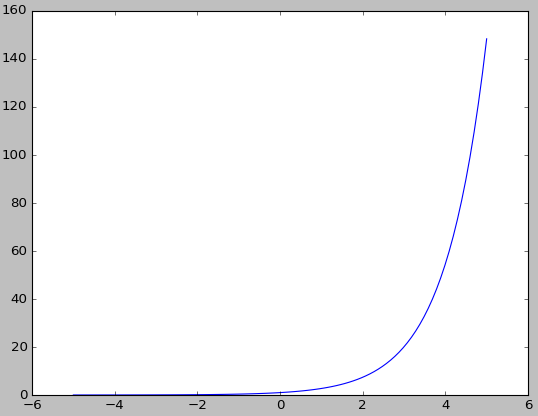
2、指数函数

exp(x)=e^x

import numpy as np
import matplotlib.pyplot as plt

def exp(x):
    return np.e**x

print exp(2)

print np.exp(2)

x = np.linspace(-5, 5, num = 100)
y = exp(x)

plt.plot(x,y)
plt.show()

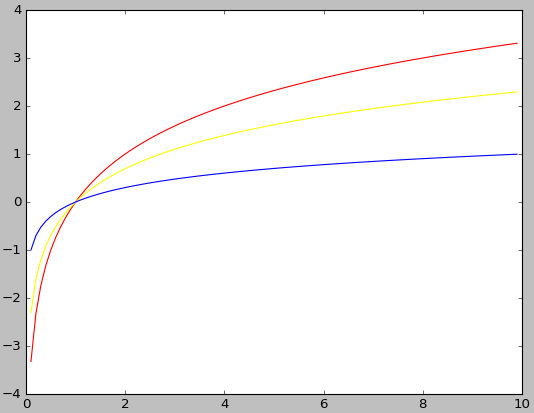
3、对数函数

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(0.1,10,99,endpoint = False)
y1 = np.log2(x)
y2 = np.log(x)
y3 = np.log10(x)
plt.plot(x,y1,'red',x,y2,'yellow',x,y3,'blue')
plt.show()

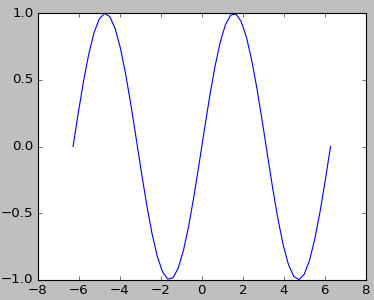
4、三角函数

sin(x)

import numpy as np
import matplotlib.pyplot as plt

plt.plot(np.linspace(-2*np.pi,2*np.pi),np.sin(np.linspace(-2*np.pi,2*np.pi)))
plt.show()

5、函数的复合

h(x)=x²+1

import numpy as np
import matplotlib.pyplot as plt

def f(x): return x+1

def g(x): return x**2

def h(x): return f(g(x))

x = np.array(range(-10,10))

y = np.array([h(i) for i in x])
plt.plot(x, y, 'bo')

# h2 = lambda x: f(g(x))
# plt.plot(x,h2(x),'rs')
plt.show()

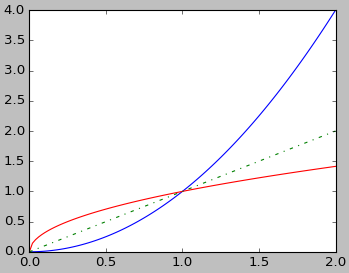
6、逆函数

w=x²

winv(x)=x^1/2

import numpy as np
import matplotlib.pyplot as plt

w = lambda x: x**2
winv = lambda x: np.sqrt(x)
x = np.linspace(0,2,100)

plt.plot(x, w(x),'b',x,winv(x),'r',x,x,'g-.')
plt.show()

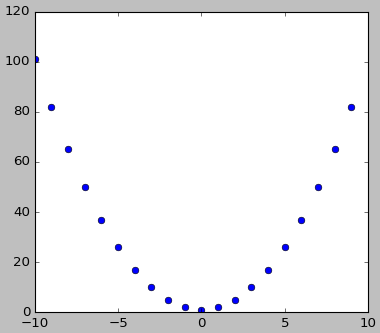
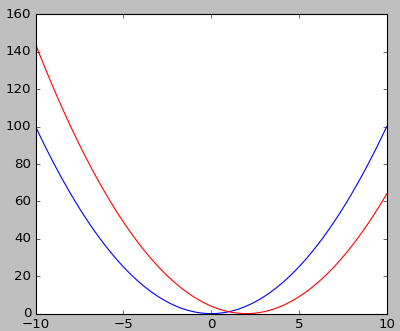
7、高阶函数

x² 和 (x-2)²

import numpy as np
import matplotlib.pyplot as plt

def g(x): return x**2

def horizontal_shift(f,H): return lambda x: f(x-H)

x = np.linspace(-10,10,100)
shifted_g = horizontal_shift(g,2)

plt.plot(x,g(x),'b',x,shifted_g(x),'r')
plt.show()

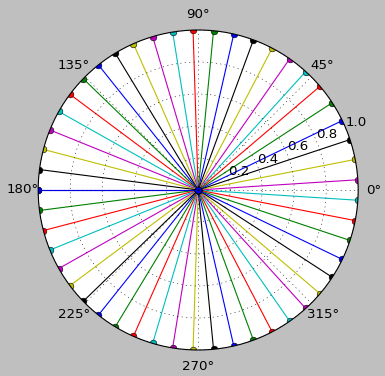
8、欧拉公式

指数函数的多项式：

$$e^x =1+\frac{x}{1!}+\frac{x^2}{2!}+\dots = \sum_{k = 0}^{\infty}\frac{x^k}{k!}$$

三角函数：

$$sin(x) = \frac{x}{1!}-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\dots = \sum_{k = 0}^{\infty}{(-1)}^k\frac{x^{(2k+1)}}{(2k+1)!}$$

$$cos(x) = \frac{x^0}{0!}-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\dots = \sum_{k = 0}^{\infty}{(-1)}^k\frac{x^{2k}}{(2k)!}$$

虚函数的基本运算规则：

$$i^0=1,\quad i^1=i,\quad i^2=-1,\quad i^3=-i$$
$$i^4=1,\quad i^5=i,\quad i^6=-1,\quad i^7=-i$$

将 ix 代入指数函数的公式中：

$$e^{ix}=\frac{(ix)^0}{0!}+\frac{(ix)^1}{1!}+\frac{(ix)^2}{2!}+\frac{(ix)^3}{3!}+\frac{(ix)^4}{4!}+\frac{(ix)^5}{5!}+\frac{(ix)^6}{6!}+\frac{(ix)^7}{7!}+\dots$$
$$\qquad =\frac{i^0x^0}{0!}+\frac{i^1x^1}{1!}+\frac{i^2x^2}{2!}+\frac{i^3x^3}{3!}+\frac{i^4x^4}{4!}+\frac{i^5x^5}{5!}+\frac{i^6x^6}{6!}+\frac{i^7x^7}{7!}+\dots$$
$$\qquad = 1\frac{x^0}{0!}+i\frac{x^1}{1!}-1\frac{x^2}{2!}-i\frac{x^3}{3!}+1\frac{x^4}{4!}+i\frac{x^5}{5!}-1\frac{x^6}{6!}-i\frac{x^7}{7!}+\dots$$
$$\qquad = (\frac{x^0}{0!}-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\dots)+i(\frac{x}{1!}-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\dots)$$
$$\qquad = cos(x)+isin(x)$$

此时便得欧拉公式：

$$e^{ix} = cos(x)+isin(x)$$

令 x=π，得：

$$e^{i\pi}+1=0$$

import numpy as np
import sympy
import matplotlib.pyplot as plt

x = np.linspace(-np.pi,np.pi)
lhs = np.e**(1j*x)
rhs = np.cos(x)+1j*np.sin(x)
print sum(lhs==rhs)==len(x)

z = sympy.Symbol('z', real = True)
sympy.expand(sympy.E**(sympy.I*z), complex = True)

for p in np.e**(1j*x):
    plt.polar([0, np.angle(p)],[0, abs(p)], marker = 'o')
plt.show()

9、泰勒级数

函数 f(x) 在 x=0 处展开的泰勒级数的定义为：

$$f(x)=f(0)+\frac{f'(0)}{1!}x+\frac{f''(0)}{2!}x^2+\frac{f'''(0)}{3!}x^3+\dots=\sum_{k=0}^{\infty}\frac{f^{(k)}(0)}{k!}x^k$$

e^x，sin(x) 和 cos(x) 的多项式形式，都是它们自己在 x=0 处展开的泰勒级数。其中 e^x 在 x=0 的展开为：

$$exp(x)=exp(0)+\frac{exp'(0)}{1!}x+\frac{exp''(0)}{2!}x^2+\frac{exp'''(0)}{3!}x^3+\dots$$
$$\qquad =1 + \frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+\dots$$
$$\qquad =\sum_{k=0}^{\infty}\frac{x^k}{k!}$$

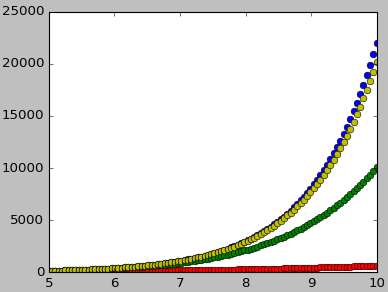
泰勒级数可以把非常复杂的函数转变成无限项的和的形式。通常，我们可以只计算泰勒级数的前几项之和，便能够获得原函数的局部近似了。在做这样的多项式近似时，我们所计算的项越多，则近似的结果越精确。

下图是 e 在 x=0 处展开的泰勒级数分别取前 5、10 和 15 项时的值跟真实值的对比，可以看出，所计算的项越多，则近似的结果越精确。

import numpy as np
import sympy
import matplotlib.pyplot as plt

x = sympy.Symbol('x')
exp = np.e**x

def polyApprox(func,num_terms):
    # 当我们需要反复做类似的步骤的时候，最好将步骤定义为一个函数
    sums = 0
    for i in range(num_terms):
        numerator = func.diff(x,i)
        numerator = numerator.evalf(subs={x:0})
        denominator = np.math.factorial(i)
        sums += numerator/denominator*x**i
    return sums

sum5 = polyApprox(exp,5)
sum10 = polyApprox(exp,10)
sum15 = exp.series(x,0,15).removeO()

xvals = np.linspace(5,10,100)
for xval in xvals:
    plt.plot(xval,exp.evalf(subs={x:xval}),'bo',\
             xval,sum5.evalf(subs={x:xval}),'ro',\
             xval,sum10.evalf(subs={x:xval}),'go',\
             xval,sum15.evalf(subs={x:xval}),'yo')

plt.show()

10、极限

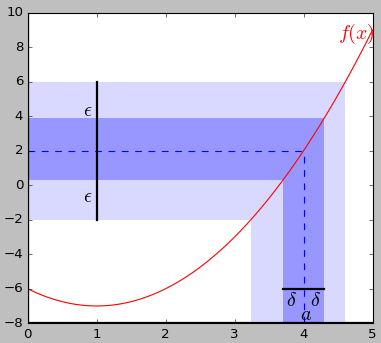
定义：若要称函数 f(x) 在 x=a 处的极限为 L，即：

$$\lim_{x\rightarrow a}f(x)=L$$

则需要：对任意一个 ε>0，都能找到 δ>0，使得当 x 的取值满足 0<|x-a|<δ 时，|f(x)-L|<ε。

import numpy as np
import sympy
import matplotlib.pyplot as plt

f = lambda x: x**2-2*x-6
x = np.linspace(0,5,100)
y = f(x)

plt.plot(x,y,'red')
plt.grid('off')

l = plt.axhline(-8,0,1,linewidth = 2, color = 'black')
l = plt.axvline(0,0,1,linewidth = 2, color = 'black')

l = plt.axhline(y=2,xmin=0,xmax=0.8,linestyle="--")
l = plt.axvline(x=4,ymin=0,ymax=float(5)/9, linestyle = "--")

l = plt.axhline(-6,3.7/5,4.3/5,linewidth = 2, color = 'black')
l = plt.axvline(1,6.0/18,14.0/18,linewidth = 2, color = 'black')

p = plt.axhspan(-2,6,0,(1+np.sqrt(13))/5,alpha = 0.15, ec = 'none')
p = plt.axvspan((1+np.sqrt(5)),(1+np.sqrt(13)),0,1.0/3,alpha = 0.15, ec = 'none')

p = plt.axhspan(f(3.7),f(4.3),0,4.3/5,alpha = 0.3, ec = 'none')
p = plt.axvspan(3.7,4.3,0,(f(3.7)+8)/18,alpha = 0.3, ec = 'none')

plt.axis([0,5,-8,10])

plt.text(0.8,-1,r"$\epsilon$", fontsize = 18)
plt.text(0.8,4,r"$\epsilon$", fontsize = 18)
plt.text(3.75,-7.0,r"$\delta$", fontsize = 18)
plt.text(4.1,-7.0,r"$\delta$", fontsize = 18)
plt.text(3.95,-7.8,r"$a$", fontsize = 18)
plt.text(4.5,8.5,r"$f(x)$", fontsize = 18,color="red")

plt.show()

现在用上面的定义来证明：

$$\lim_{x\rightarrow 4}x^2-2x-6=2$$

即对于任意的 ε>0，能找到一个 δ>0，使得 0<|x-4|<δ 时，有 |f(x)-2|<ε。

证明：注意到 |f(x)-2|=|x²-2x-6-2|=|(x-4)(x+2)|=|x-4|·|x+2|，已知 |x-4|<δ，根据三角形不等式，|x+2|=|x-4+6|≤|x-4|+6<δ+6，所以

|f(x)-2|=|x-4|·|x+2|<δ·(δ+6)，现在只需找到一个 δ，满足 δ·(δ+6)<ε 即可，用二元一次方程知识就可以证明这样的 δ>0 是存在的。

或者只要令 δ=min(1,ε/7)，即可使得 δ≤ε/7 且 δ+6≤7，使得 δ·(δ+6)<ε。

11、泰勒级数用于极限计算

我们在中学课本中一定记忆了常见的极限，以及极限计算的规则，这里我们便不再赘言。泰勒级数也可以用于计算一些形式比较复杂的函数的极限。这里，仅举一例：

$$\lim_{x\rightarrow 0}\frac{sin(x)}{x}=\lim_{x\rightarrow 0}{\frac{\frac{x}{1!}-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\dots}{x}}$$

$$\qquad = \lim_{x\rightarrow 0}{\frac{x(1-\frac{x^2}{3!}+\frac{x^4}{5!}-\frac{x^6}{7!}+\dots)}{x}}$$

$$\qquad = \lim_{x\rightarrow 0}{1-\frac{x^2}{3!}+\frac{x^4}{5!}-\frac{x^6}{7!}+\dots}$$

$$\qquad = 1$$

12、洛必达法则

利用泰勒级数来计算极限，有时也会陷入困境，例如：求极限的位置是在我们不知道泰勒展开的位置，或者所求极限是无穷的。通常遇到这些情况我们会使用各种形式的洛必达法则。

这里我们仅尝试说明

$$\frac{0}{0}$$

形式的洛必达法则为何成立。

如果 f 和 g 是连续函数，且

$$\lim_{x\rightarrow a}f(x)=0,\quad \lim_{x\rightarrow a}g(x)=0$$

若

$$\lim_{x\rightarrow a}\frac{f'(x)}{g'(x)}$$

存在，则：

$$\lim_{x\rightarrow a}\frac{f(x)}{g(x)}=\lim_{x\rightarrow a}\frac{f'(x)}{g'(x)}$$

如果分子分母求导后仍然是 0/0 形式，那么重复该过程，直至问题解决。

运用泰勒级数，我们很容易可以理解洛必达法则为什么会成立：

$$\lim_{x\rightarrow a}{\frac{f(x)}{g(x)}}=\lim_{x\rightarrow a}{\frac{f(a)+\frac{f'(a)}{1!}(x-a)+\frac{f''(a)}{2!}(x-a)^2+\frac{f'''(a)}{3!}(x-a)^3+\dots}{g(a)+\frac{g'(a)}{1!}(x-a)+\frac{g''(a)}{2!}(x-a)^2+\frac{g'''(a)}{3!}(x-a)^3+\dots}}$$

$$\qquad = \lim_{x\rightarrow a}{\frac{\frac{f'(a)}{1!}(x-a)+\frac{f''(a)}{2!}(x-a)^2+\frac{f'''(a)}{3!}(x-a)^3+\dots}{\frac{g'(a)}{1!}(x-a)+\frac{g''(a)}{2!}(x-a)^2+\frac{g'''(a)}{3!}(x-a)^3+\dots}}$$

$$\qquad =\lim_{x\rightarrow a}{\frac{f'(a)+\frac{f''(a)}{2!}(x-a)+\frac{f'''(a)}{3!}(x-a)^2+\dots}{g'(a)+\frac{g''(a)}{2!}(x-a)+\frac{g'''(a)}{3!}(x-a)^2+\dots}}$$

$$\qquad = \lim_{x\rightarrow a}\frac{f'(x)}{g'(x)}$$

参考资料：

[1] https://ryancheunggit.gitbooks.io/calculus-with-python/content/