如何在 Java 中实现 Dijkstra 最短路算法

定义

最短路问题的定义为：设 \(G=(V,E)\) 为连通图，图中各边 \((v_i,v_j)\) 有权 \(l_{ij}\) （\(l_{ij}=\infty\) 表示 \(v_i,v_j\) 间没有边） ，\(v_s,v_t\) 为图中任意两点，求一条道路 \(\mu\)，使得它是从 \(v_s\) 到 \(v_t\) 的所有路中总权最小的路，即：\(L(\mu)=\sum_{(v_i,v_j)\in \mu}l_{ij}\) 最小。

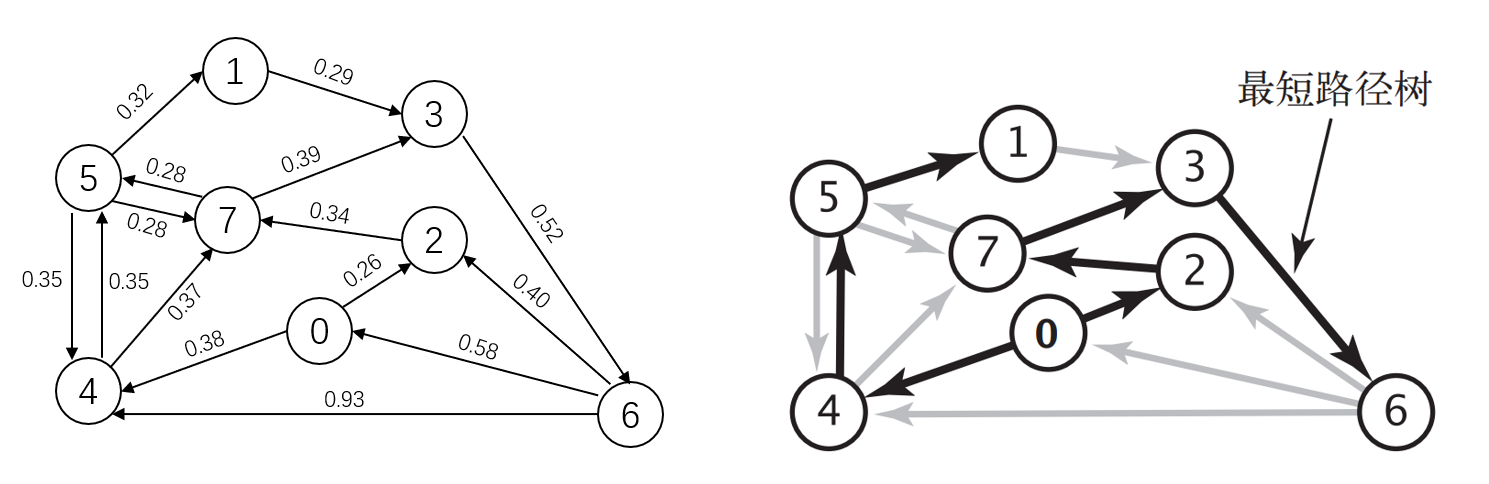
下图左侧是一幅带权有向图，以顶点 0 为起点到各个顶点的最短路径形成的最短路径树如下图右侧所示：

带权有向图的实现

在实现最短路算法之前需要先实现带权有向图。在上一篇博客 《如何在 Java 中实现最小生成树算法》 中我们实现了带权无向图，只需一点修改就能实现带权有向图。

带权有向边

首先应该实现带权有向图中的边 DirectedEdge，这个类有三个成员变量：指出边的顶点 v、边指向的顶点 w 和边的权重 weight。代码如下所示：

package com.zhiyiyo.graph;

/**
 * 带权有向边
 */
public class DirectedEdge {
    int v, w;
    double weight;

    public DirectedEdge(int v, int w, double weight) {
        this.v = v;
        this.w = w;
        this.weight = weight;
    }

    public int from() {
        return v;
    }

    public int to() {
        return w;
    }

    public double getWeight() {
        return weight;
    }

    @Override
    public String toString() {
        return String.format("%d->%d(%.2f)", v, w, weight);
    }
}

带权有向图

带权有向图的实现非常简单，只需将带权无向图使用的 Edge 类换成 DirectedEdge 类，并作出少许调整即可：

package com.zhiyiyo.graph;

import com.zhiyiyo.collection.stack.LinkStack;
import com.zhiyiyo.collection.stack.Stack;

public class WeightedDigraph {
    private final int V;
    protected int E;
    protected LinkStack<DirectedEdge>[] adj;

    public WeightedDigraph(int V) {
        this.V = V;
        adj = (LinkStack<DirectedEdge>[]) new LinkStack[V];
        for (int i = 0; i < V; i++) {
            adj[i] = new LinkStack<>();
        }
    }

    public int V() {
        return V;
    }

    public int E() {
        return E;
    }

    public void addEdge(DirectedEdge edge) {
        adj[edge.from()].push(edge);
        E++;
    }

    public Iterable<DirectedEdge> adj(int v) {
        return adj[v];
    }

    public Iterable<DirectedEdge> edges() {
        Stack<DirectedEdge> edges = new LinkStack<>();
        for (int v = 0; v < V; ++v) {
            for (DirectedEdge edge : adj(v)) {
                edges.push(edge);
            }
        }

        return edges;
    }
}

最短路算法

API

最短路算法应该支持起始点 \(v_s\) 到任意顶点 \(v_t\) 的最短距离和最短路径的查询：

package com.zhiyiyo.graph;

/**
 * 最短路径
 */
public interface ShortestPath {
    /**
     * 从起点到顶点 v 的最短距离，如果顶点 v 不可达则为无穷大
     * @param v 顶点 v
     * @return 最短路径
     */
    double distTo(int v);

    /**
     * 是否存在从起点到顶点 v 的路径
     * @param v 顶点 v
     * @return 是否存在
     */
    boolean hasPathTo(int v);

    /**
     * 从起点到顶点 v 的最短路径，若不存在则返回 null
     * @param v 顶点 v
     * @return 最短路径
     */
    Iterable<DirectedEdge> pathTo(int v);
}

Dijkstra 算法

我们可以使用一个距离数组 distTo[] 来保存起始点 \(v_s\) 到其余顶点 \(v_t\) 的最短路径，且 distTo[] 数组满足以下条件：

\[distTo(t) = \left\{ \begin{aligned} 0 \quad & t=s \\ l_{st} \quad & t\neq s 且\ t\ 可达\\ \infty \quad & t\ 不可达 \end{aligned} \right. \]

可以使用 Double.POSITIVE_INFINITY 来表示无穷大，有了 distTo[] 之后就能实现 ShortestPath 前两个方法：

package com.zhiyiyo.graph;

public class DijkstraSP implements ShortestPath {
    private double[] distTo;

    @Override
    public double distTo(int v) {
        return distTo[v];
    }

    @Override
    public boolean hasPathTo(int v) {
        return distTo[v] < Double.POSITIVE_INFINITY;
    }
}

为了保存 \(v_s\) 到 \(v_t\) 的最短路径，可以使用一个边数组 edgeTo[]，其中 edgeTo[v] = e_wv 表示要想到达 \(v_t\)，需要先经过顶点 \(v_w\)，接着从 edgeTo[w]获取到达 \(v_w\) 之前需要到达的上一个节点，重复上述步骤直到发现 edgeTo[i] = null，这时候就说明我们回到了 \(v_s\)。 获取最短路径的代码如下所示：

@Override
public Iterable<DirectedEdge> pathTo(int v) {
    if (!hasPathTo(v)) return null;
    Stack<DirectedEdge> path = new LinkStack<>();
    for (DirectedEdge e = edgeTo[v]; e != null; e = edgeTo[e.from()]) {
        path.push(e);
    }
    return path;
}

算法流程

虽然我们已经实现了上述接口，但是如何得到 distTo[] 和 edgeTo[] 还是个问题，这就需要用到 Dijkstra 算法了。算法的思想是这样的：

1. 初始化 distTo[] 使得除了 distTo[s] = 0 外，其余的元素都为 Double.POSITIVE_INFINITY。同时初始化 edgeTo[] 的每个元素都是 null；

2. 将顶点 s 的所有相邻顶点 \(v_j\) 加入集合 \(V'\) 中，设置 distTo[j] = l_sj 即初始化最短距离为邻边的权重；

3. 从 \(V'\) 中取出距离最短即 distTo[m] 最小的顶点 \(v_m\)，遍历 \(v_m\) 的所有邻边 \((v_m, v_w)\)，如果有 \(l_{mw}+l_{sm}<l_{sw}\)，就说明从 \(v_s\) 走到 \(v_m\) 再一步走到 \(v_w\) 距离最短，我们就去更新 distTo[m]，同时将 \(v_w\) 添加到 \(V'\) 中（如果 \(v_w\) 不在的话）；

4. 重复上述过程直到 \(V'\) 变为空，我们就已经找到了所有 \(v_s\) 可达的顶点的最短路径。

上述过程中有个地方会影响算法的性能，就是如何从 \(V'\) 中取出最小距离对应的顶点 \(v_m\)。如果直接遍历 \(V'\) 最坏情况下时间复杂度为 \(O(|V|)\)，如果换成最小索引优先队列则可以将时间复杂度降至 \(O(\log|V|)\)。

最小索引优先队列

上一篇博客 《如何在 Java 中实现最小生成树算法》 中介绍了最小堆的使用，最小堆可以在对数时间内取出数据集合中的最小值，对应到最短路算法中就是最短路径。但是有一个问题，就是我们想要的是最短路径对应的那个顶点 \(v_m\)，只使用最小堆是做不到这一点的。如何能将最小堆中的距离值和顶点进行绑定呢？这就要用到索引优先队列。

索引优先队列的 API 如下所示，可以看到每个元素 item 都和一个索引 k 进行绑定，我们可以通过索引 k 读写优先队列中的元素。想象一下堆中的所有元素放在一个数组 pq 中，索引优先队列可以做到在对数时间内取出 pq 的最小值。

package com.zhiyiyo.collection.queue;

/**
 * 索引优先队列
 */
public interface IndexPriorQueue<K extends Comparable<K>> {
    /**
     * 向堆中插入一个元素
     *
     * @param k 元素的索引
     * @param item 插入的元素
     */
    void insert(int k, K item);

    /**
     * 修改堆中指定索引的元素值
     * @param k 元素的索引
     * @param item 新的元素值
     */
    void change(int k, K item);

    /**
     * 向堆中插入或修改元素
     * @param k 元素的索引
     * @param item 新的元素值
     */
    void set(int k, K item);

    /**
     * 堆是否包含索引为 k 的元素
     * @param k 索引
     * @return 是否包含
     */
    boolean contains(int k);

    /**
     * 弹出堆顶的元素并返回其索引
     * @return 堆顶元素的索引
     */
    int pop();

    /**
     * 弹出堆中索引为 k 为元素
     * @param k 索引
     * @return 索引对应的元素
     */
    K delete(int k);

    /**
     * 获取堆中索引为 k 的元素，如果 k 不存在则返回 null
     * @param k 索引
     * @return 索引为 k 的元素
     */
    K get(int k);

    /**
     * 获取堆中的元素个数
     */
    int size();

    /**
     * 堆是否为空
     */
    boolean isEmpty();
}

实现索引优先队列比优先队列麻烦一点，因为需要维护每个元素的索引。之前我们是将元素按照完全二叉树的存放顺序进行存储，现在可以换成索引，而元素只需根据索引值 k 放在数组 keys[k] 处即可。只有索引数组 indexes[] 和元素数组 keys[] 还不够，如果我们想实现 contains(int k) 方法，目前只能遍历一下 indexes[]，看看 k 在不在里面，时间复杂度是 \(O(|V|)\)。何不多维护一个数组 nodeIndexes[]，使得它满足下述关系：

\[\text{nodeIndexes}(k) = \left\{ \begin{aligned} d \quad & k \in \text{indexes} \\ -1 \quad & k \notin \text{indexes} \end{aligned} \right. \]

如果能在 nodeIndexes[k] 不是 -1，就说明索引 \(k\) 对应的元素存在与堆中，且索引 k 在 indexes[] 中的位置为 \(d\)，即有下述等式成立：

\[\text{indexes}[\text{nodeIndexes}[k]] = k\\ \text{nodeIndexes}[\text{indexes}[d]] = d \]

有了这三个数组之后我们就可以实现最小索引优先队列了：

package com.zhiyiyo.collection.queue;

import java.util.Arrays;
import java.util.NoSuchElementException;

/**
 * 最小索引优先队列
 */
public class IndexMinPriorQueue<K extends Comparable<K>> implements IndexPriorQueue<K> {
    private K[] keys;           // 元素
    private int[] indexes;      // 元素的索引，按照最小堆的顺序摆放
    private int[] nodeIndexes;  // 元素的索引在完全二叉树中的编号
    private int N;

    public IndexMinPriorQueue(int maxSize) {
        keys = (K[]) new Comparable[maxSize + 1];
        indexes = new int[maxSize + 1];
        nodeIndexes = new int[maxSize + 1];
        Arrays.fill(nodeIndexes, -1);
    }

    @Override
    public void insert(int k, K item) {
        keys[k] = item;
        indexes[++N] = k;
        nodeIndexes[k] = N;
        swim(N);
    }

    @Override
    public void change(int k, K item) {
        validateIndex(k);
        keys[k] = item;
        swim(nodeIndexes[k]);
        sink(nodeIndexes[k]);
    }

    @Override
    public void set(int k, K item) {
        if (!contains(k)) {
            insert(k, item);
        } else {
            change(k, item);
        }
    }

    @Override
    public boolean contains(int k) {
        return nodeIndexes[k] != -1;
    }

    @Override
    public int pop() {
        int k = indexes[1];
        delete(k);
        return k;
    }

    @Override
    public K delete(int k) {
        validateIndex(k);
        K item = keys[k];
        // 交换之后 nodeIndexes[k] 发生变化，必须先保存为局部变量
        int nodeIndex = nodeIndexes[k];
        swap(nodeIndex, N--);
        // 必须有上浮的操作，交换后的元素可能比上面的元素更小
        swim(nodeIndex);
        sink(nodeIndex);
        keys[k] = null;
        nodeIndexes[k] = -1;
        return item;
    }

    @Override
    public K get(int k) {
        return contains(k) ? keys[k] : null;
    }

    public K min() {
        return keys[indexes[1]];
    }

    /**
     * 获取最小的元素对应的索引
     */
    public int minIndex() {
        return indexes[1];
    }

    @Override
    public int size() {
        return N;
    }

    @Override
    public boolean isEmpty() {
        return N == 0;
    }

    /**
     * 元素上浮
     *
     * @param k 元素的索引
     */
    private void swim(int k) {
        while (k > 1 && less(k, k / 2)) {
            swap(k, k / 2);
            k /= 2;
        }
    }

    /**
     * 元素下沉
     *
     * @param k 元素的索引
     */
    private void sink(int k) {
        while (2 * k <= N) {
            int j = 2 * k;
            // 检查是否有两个子节点
            if (j < N && less(j + 1, j)) j++;
            if (less(k, j)) break;
            swap(k, j);
            k = j;
        }
    }

    /**
     * 交换完全二叉树中编号为 a 和 b 的节点
     *
     * @param a 索引 a
     * @param b 索引 b
     */
    private void swap(int a, int b) {
        int k1 = indexes[a], k2 = indexes[b];
        nodeIndexes[k2] = a;
        nodeIndexes[k1] = b;
        indexes[a] = k2;
        indexes[b] = k1;
    }

    private boolean less(int a, int b) {
        return keys[indexes[a]].compareTo(keys[indexes[b]]) < 0;
    }

    private void validateIndex(int k) {
        if (!contains(k)) {
            throw new NoSuchElementException("索引" + k + "不在优先队列中");
        }
    }
}

注意对比最小堆和最小索引堆的 swap(int a, int b) 方法以及 less(int a, int b) 方法，在交换堆中的元素时使用的依据是元素的大小，交换之后无需调整 keys[]，而是交换 nodeIndexes[] 和 indexes[] 中的元素。

实现算法

通过上述的分析，实现 Dijkstra 算法就很简单了，时间复杂度为 \(O(|E|\log |V|)\)：

package com.zhiyiyo.graph;

import com.zhiyiyo.collection.queue.IndexMinPriorQueue;
import com.zhiyiyo.collection.stack.LinkStack;
import com.zhiyiyo.collection.stack.Stack;

import java.util.Arrays;

public class DijkstraSP implements ShortestPath {
    private double[] distTo;
    private DirectedEdge[] edgeTo;
    private IndexMinPriorQueue<Double> pq;
    private int s;

    public DijkstraSP(WeightedDigraph graph, int s) {
        pq = new IndexMinPriorQueue<>(graph.V());
        edgeTo = new DirectedEdge[graph.V()];

        // 初始化距离
        distTo = new double[graph.V()];
        Arrays.fill(distTo, Double.POSITIVE_INFINITY);
        distTo[s] = 0;

        visit(graph, s);
        while (!pq.isEmpty()) {
            visit(graph, pq.pop());
        }
    }

    private void visit(WeightedDigraph graph, int v) {
        for (DirectedEdge edge : graph.adj(v)) {
            int w = edge.to();
            if (distTo[w] > distTo[v] + edge.getWeight()) {
                distTo[w] = distTo[v] + edge.getWeight();
                edgeTo[w] = edge;
                pq.set(w, distTo[w]);
            }
        }
    }

    // 省略已实现的方法 ...
}

后记

Dijkstra 算法还能继续优化，将最小索引堆换成斐波那契堆之后时间复杂度为 \(O(|E|+|V|\log |V|)\)，这里就不写了（因为还没学到斐波那契堆），以上~~