ABC266.

D

设 \(f_{t,p}\) 代表在 \(t\) 时间点时人在 \(p\) 点的最大收益，在这一步他可以 \(p\) 增加，不动，\(p\) 减少。于是得出状态转移方程：\(f_{t,p} = \max(f_{t-1,p-1}, f_{t-1,p}, f_{t-1,p+1}) + a_{t,p}\)。

E

设 \(f_i\) 是第 \(i\) 轮的最大收益，策略一定是当骰子点数 \(\geq x\) 时就停止（\(x\) 是枚举的），则有 \(\dfrac{x-1}{6}\) 的概率重摇，而停止的期望是 \(\dfrac{x+(x+1)+\cdots+6}{6}=\dfrac{(6-x)(7+x)/2}{6}\)，所以有 \(f_i=\dfrac{(x-1)f_{i+1}+(6-x)(7+x)/2}{6}\)。

F

构成一个环套树，搜出那个环，将所有节点是环上哪个节点的子树搜出来，然后判断两个节点的根是否相等。

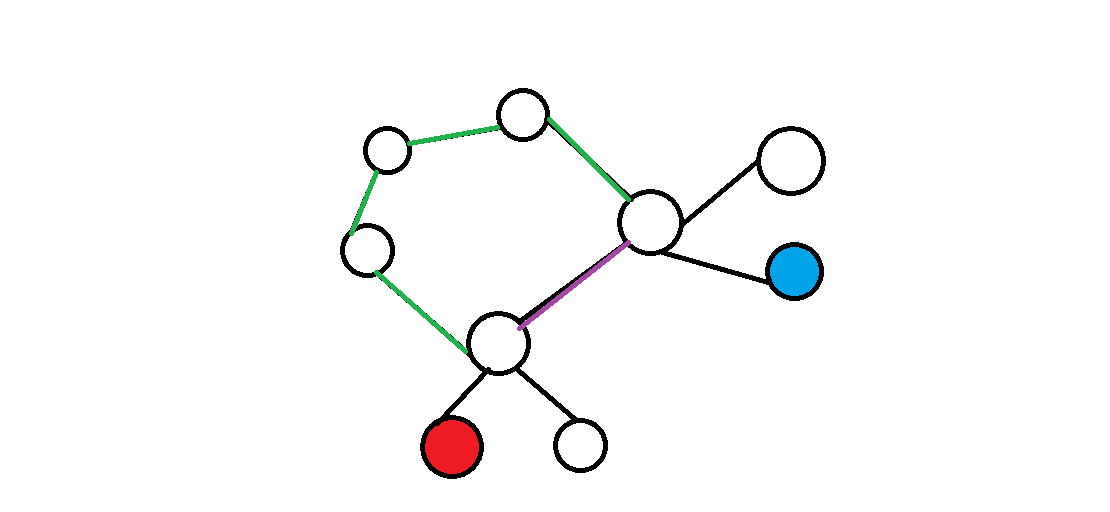
在本图中，先把所有节点返到环上，于是有两条路径，输出 No。



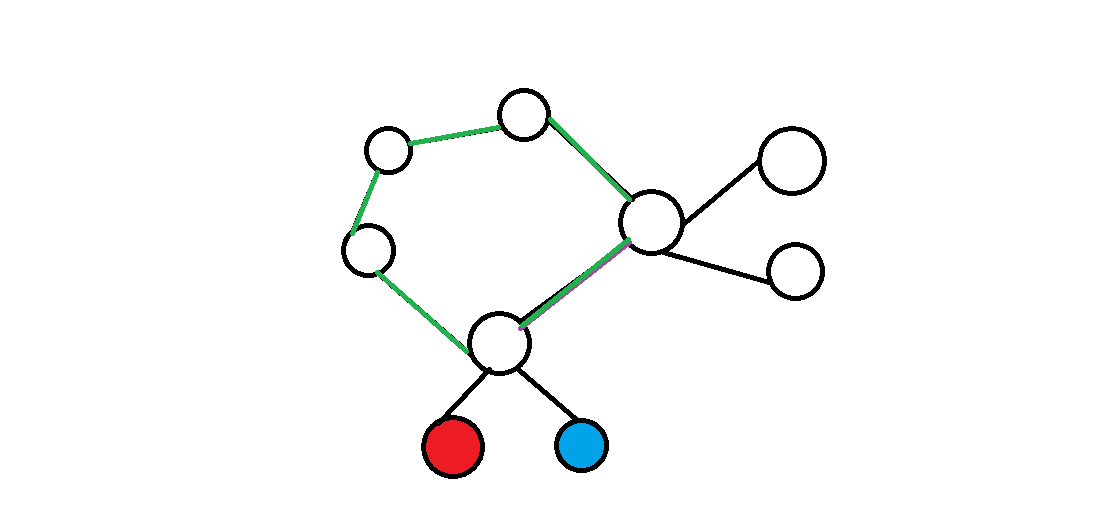
在本图中，返到换上后必须绕一圈才能有第二条路径，而绕一圈就不是 simple path 了，于是输出 Yes。

G

令 \({\tt RG}={\tt X}\)，则问题转化为 \(R-K\) 个 \({\tt R}\)，\(G-K\) 个 \({\tt G}\)，\(B\) 个 \({\tt B}\)，\(K\) 个 \({\tt X}\)，要求 \({\tt RG}\) 不能相邻，于是插板法可以解决问题。

H

通过 dp 得到 \(f_{i,x,y}=\max\{f_{i',x',y'} : y' \le y \wedge |x - x'| + y - y' \le t - t'\}\)。

有一个讨厌的绝对值，考虑消掉他。

\(
\begin{array}{l}
|x - x'| + y - y' \le t - t' \\
|x - x'| \le (t - t') - (y - y') \\
\{|x - x'|, -|x - x'|\} = \{x, -x\} \\
-|x - x'| \le 0 \le (t - t') - (y - y') & (y - y') \le 0, (t - t') \ge (t - t') - (y - y') \ge 0 \\
|x - x'| \le k \\
|x - x'| \le k \wedge -|x - x'| \le k \\
(x - x') \le k \wedge -(x - x') \le k
\end{array}
\)

于是有 \((x-x')+(y-y') \le (t-t') \wedge (x'-x) + (y-y') \le (t-t')\)，于是移项得 \((t'-x'-y') \le (t-x-y) \wedge (t'+x'-y') \le (t+x+y)\)，再加上 \(y' \le y\)，就是春春的三位偏序，就可以 \(\rm cdq\) 解决。