2021春季学期华清大学EE数算OJ3：岩石的重量

原题目如下：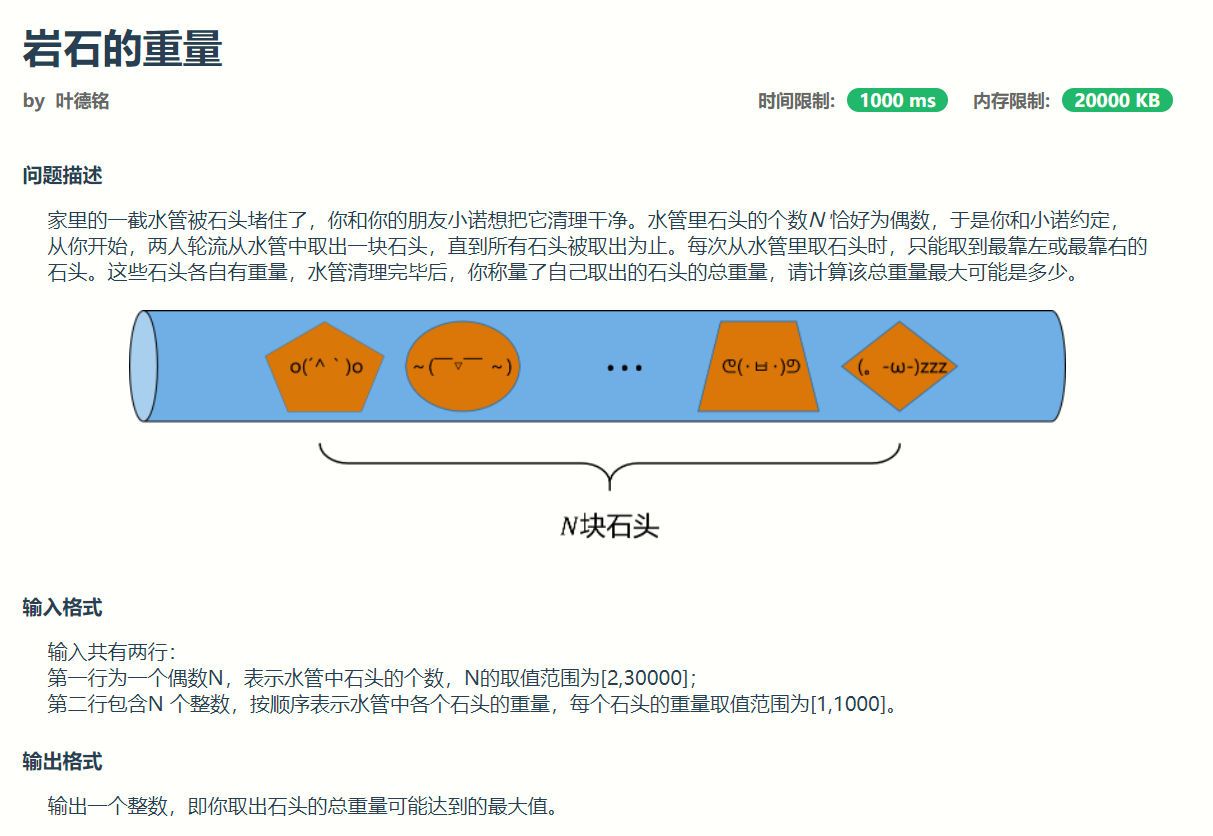

看起来，这不过是我们在《程序设计基础》里面接触过的简单动态规划问题（
什么，你不知道什么叫动态规划？

什么是动态规划？

百度百科对“动态规划”一词定义如下：在现实生活中，有一类活动的过程，由于它的特殊性，可将过程分成若干个互相联系的阶段，在它的每一阶段都需要作出决策，从而使整个过程达到最好的活动效果。因此各个阶段决策的选取不能任意确定，它依赖于当前面临的状态，又影响以后的发展。当各个阶段决策确定后，就组成一个决策序列，因而也就确定了整个过程的一条活动路线．这种把一个问题看作是一个前后关联具有链状结构的多阶段过程就称为多阶段决策过程，这种问题称为多阶段决策问题。在多阶段决策问题中，各个阶段采取的决策，一般来说是与时间有关的，决策依赖于当前状态，又随即引起状态的转移，一个决策序列就是在变化的状态中产生出来的，故有“动态”的含义，称这种解决多阶段决策最优化的过程为动态规划方法 。
但这样的定义谁也读不下去不是吗，因此，思考这样一个问题：
《程序设计基础》中，老师曾经讲过，对于“求斐波那契数列”这道题，用递推的办法比递归的办法更快。我们分别分析一下这两种办法。
假设我们需要求解f(6),对于递推法，我们只需要求解f5+f4，且这两者已经被我们求出来了。而对于递归法，f5和f4需要我们再调用函数求解，他们分别的求解过程中还需要继续套娃。。。
比较两种方法，我们不难发现，递推法把问题分成了若干小问题，而对于部分问题的解进行了存储，这样就使得如果我们希望多次调用一个中间值，无需反复递归求解。这就是一种dp（动态规划）的思想。
以这道题为例，我们就可以存储下每次取完石头后，对于不同位置的重量最大值，这样在进行下一步时，无需进行反复的递归。

用朴素的dp思想试做这道题

原题中对dp思想给予的温馨提示：

（其实这个提示已经将dp的具体实现告诉大家了）
读者可以自己尝试根据上述提示写出一个dp程序。
之所以这样dp，是因为如果确定了i轮选择和左边取出j个石头，无论前i-1的选择情况是怎样的，都不会对后续选择造成任何影响。

如果自己不能写出这个dp程序，下面是几点提示：
1.找到动态规划状态转移方程。dp就是由初始状态，边界条件，停止条件和状态转移方程组成的。对于这道题来说，在每个地方的状态转移方程都是等价的，没有什么特殊的干扰条件。
2.上述的i，j其实提示了实现循环的方法，可以发现按照这两个循环变量进行循环，恰好没有丢失或多步骤，而且步骤的顺序是满足本身的因果关系的。
3.最终得到的是一个一维数组，存储了左指针（j）在各个位置的选取最优解。只需在这些最优解中再取最优解即可。
如果你写出了这个dp程序，你会发现并不能够ac此题，而且，出现了一种罕见的错误类型，叫做：

如何降低空间复杂度？

本题的内存限制为20000kb，显然，并不能支撑我们开启1000*1000的二维数组。这就考验我们能否将空间复杂度进一步降低呢？
其实本题用到的优化也是在dp中非常常见的：我们发现，在状态转移方程中，第i轮的数值永远只和第i-1轮相关，而且我们在更新的时候，也是按照i的增加顺序更新的，也就是说，在更新第i次选取时，第i-2及以前的数据，我们是已经用不到的。这也就是说，我们可以用两个一维数组循环求解来代替原来的二维数组。
为了书写方便，我采用了一个第二维大小为2的二维数组。代码如下

#include<cstdio>
#include<algorithm>
#include<cstdlib>
#include<string>
using namespace std;
int d[2][30005],g[30005];
inline void read(int&x){
    char c,f=x=0;
    while(!isdigit(c=getchar()))f=c=='-';
    while(isdigit(c))x=x*10-48+c,c=getchar();
    if(f)x=-x;
}
int main(){
    int n;scanf("%d",&n);
    for(int i=1;i<=n;i++)read(g[i]);
    int p=0;
    for(int k=1;k<=n/2;k++){
        int q=p^1;
        for(int r=0;r<=2*k;r++){   //左指针为r，即第r个石头在第k次后被取走了
            if(!r)d[q][r]=d[p][r]+g[r+n+2-2*k];
            else if(r==1)d[q][r]=max(d[p][r]+g[r+n+2-2*k],d[p][r-1]+max(g[r],g[r+n-2*k+1]));
            else if(r==2*k-1)d[q][r]=max(d[p][r-1]+max(g[r],g[r+n-2*k+1]),d[p][r-2]+g[r-1]);
            else if(r==2*k)d[q][r]=d[p][r-2]+g[r-1];
            else d[q][r]=max(d[p][r-1]+max(g[r],g[r+n-2*k+1]),max(d[p][r-2]+g[r-1],d[p][r]+g[r+n+2-2*k]));
        }
        p=p^1;
    }
    int ma=0,k=n/2;
    for(int i=2;i<=n+1;i++){ma=ma>d[k&1][i]?ma:d[k&1][i];}
    printf("%d",ma);
}

（依然采用了快读，喜提472ms）
（求广大dalao教教如何进一步优化）