Datawhale组队学习_Task02：详读西瓜书+南瓜书第3章

第3章 线性模型

家人们又来吃瓜了！

3.1 基本形式

线性模型的本质是通过一个所有属性的线性组合进行预测的函数，即

$\mathcal{f(x)=w_1x_1+w_2x_2+...+w_dx_d+b}$
一般用向量形式写成
$\mathcal{f(x)=w^Tx+b}$
其中$\mathcal{w}$直观表达了个属性在预测中的重要性。

3.2 线性回归

从最简单的单属性的情形入手。若属性值之间存在“序”关系。可将其连续化转化为连续值，如“身高”的取值“高”“矮”可以转化为{1.0，0.0}。

若属性之间不存在序关系，则需将其转化为\(\mathcal{k}\)维向量。斤首先我们需要明晰：我们最终想要做到的是通过线性回归最终学得

$\mathcal{f(x_i)=wx_i+b}$,使得$\mathcal{f(x_i)≈y_i}$
而在此式中，未知量是$\mathcal{w,b}$,所以线性回归得最终目标应该就是使得学习器中二者的误差最小，以使得最终的学习结果更加接近于真实值。这里我们使用**均方误差**来作为其性能度量，即
$\mathcal{(w^*,b^*)=arg min\sum_{i=1}^m{(f(x_i)-y_i)^2}=arg min\sum_{i=1}^m{(y_i-wx_i-b)^2}}$

通过对\(\mathcal{w，b}\)求导，我们可以得到

$\mathcal{\frac{\partial E_(w,b)}{\partial w}=2(w\sum_{i=1}^m{x_i^2}-\sum_{i=1}^m{(y_i-b)x_i})}$


$\mathcal{\frac{\partial E_(w,b)}{\partial b}=2(mb-\sum_{i=1}^m{(y_i-wx_i)}}$

进而令偏导数为0，我们就可以得到\(\mathcal{w}\)和\(\mathcal{b}\)最优解

$\mathcal{w=\frac{\sum_{i=1}^m{y_1(x_i-\overline{x})}}{\sum_{i=1}^m{x_i^2}-\frac{1}{m}(\sum_{i=1}^m{x_i})^2}}$


$\mathcal{b=\frac{1}{m}\sum_{i=1}^m(y_i-wx_i)}$

而更一般的情况是，样本是由\(\mathcal{d}\)个元素来描述的，这时也就是“多元线性回归”，同理，我们可以用最小二乘法来对\(\mathcal{w,b}\)来进行估计。为便于讨论，我们把\(\mathcal{w}\)和\(\mathcal{b}\)吸收入向量形式\(\mathcal{\hat w=(w;b)}\)，相应的，把数据集D可以表示为\(\mathcal{m×(d+1)}\)大小的矩阵X，即

\[X=
\left\{
\begin{matrix}
x_{11} & x_{12} & \cdots & x_{1d} & 1\\
x_{21} & x_{22} & \cdots & x_{2d} & 1\\
\vdots & \vdots & \ddots & \vdots & 1\\
x_{m1} & x_{m2} & \cdots & x_{md} & 1\\
\end{matrix}
\right\}
=
\left\{
\begin{matrix}
x_1^T & 1\\
x_2^t & 1\\
\vdots & \vdots\\
x_m^T & 1\\
\end{matrix}
\right\}
\]

则此时“唯一的”未知量即为\(\mathcal{\hat w}\)，类似的有

${\hat w^*=arg min(y-X\hat w)^T(y-X\hat w)}$
对$\mathcal{\hat w}$求导得到
${\frac{\partial E_\hat w}{\partial \hat w}=2X^T(X\hat w-y)}$
令上式为零可以得到$\mathcal{\hat w}$最优解的闭式解，可以进行一个简单的讨论。

当\(X^TX\)为满秩矩阵或正定矩阵式，令上式为零可以得到

${\hat w^*=(X^TX)^{-1}X^Ty}$

这里的解法还需要学习一下，矩阵解法已经完全还给老师了！

则最终学得的多元线性回归模型为

${f(\hat x_i)=\hat x_i^T(X^TX)^{-1}X^Ty}$

但现实任务中往往不是那么容易就会出现满秩矩阵，其属性数目超过样例数的情况也是大有存在，这时也就需要引入正则化项来决定学习算法的归纳偏好

广义线性模型：考虑单调可微函数g(·)，令

${y=g^{-1}(w^{T}x+b)}$
  这样得到的模型称为“广义线性模型”，其中g(·)称为“联系函数”。

3.3 对数几率回归

  在处理分类任务时，可以找一个单调可微函数将分类任务的真实标记y与线性回归模型的预测值联系起来。

  若仅考虑二分类任务，则其输出标记y∈{0，1}，而线性回归模型产生的预测值是实值，故需要进行一个转换，最理想的是“单位阶跃函数”。

\[y=
\begin{cases}
0 ,z<0; \\
0.5 ,z=0;(表示可以任判) \\
1 ,z>0,
\end{cases}
\]

  为能够代入到广义线性模型中，我们需要一个类似的单点可微函数，也就有了这样一个替代函数：

${y=\frac{1}{1+e^{-z}}}$
  带入“广义线性模型”则有：
${y=\frac{1}{1+e^{-(w^Tx+b)}}}$
则做对数变换有：
${ln\frac{y}{1-y}=w^Tx+b}$
若将y视为样本x作为正例的可能性，则1-y是其反例可能性，两者的比值（即等号左对数部分内容）称为“几率”，反映了**x作为正例的相对可能性**

优点：

直接对分类可能性进行建模，无需实现假设数据分布，可以避免假设分布不准确带来的问题

可以得到近似概率预测

是对率函数任意阶可导

3.4 线性判别分析(LDA)

  主要思想：给定训练样例集，设法将样例投影到一条直线(\({y=w^Tx}\))上，使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离；在对新样本进行分类时，将其投影到同样的这条直线上，再根据投影点的未知来确定新样本的类别。即如图所示：



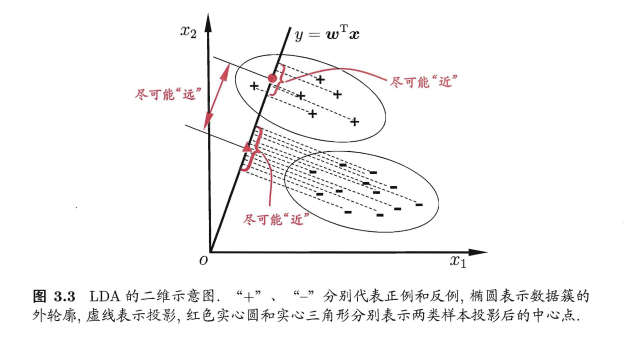
  若给定数据集D=\({{(x_i,y_i)}^m_{i=1},y_i∈{0,1}}\)，令\({X_i,M_i,\sum_i}\)分别表示示例的集合、均值向量、协方差矩阵。若想达到分类的目的，从图像的角度想要达到的是使同类样例的投影点尽可能接近，即让同类样例投影点的协方差(\({w^T\sum_0w+b^T\sum_1w}\))尽可能小，以及让异类样例的投影点尽可能远离，即让类中心之间的距离(\({∣∣w^TM_0-w^TM_1∣∣^2_2}\))尽可能大，则同时考虑二者，我们可以得到最大化目标：

${J=\frac{∣∣w^TM_0-w^TM_1∣∣^2_2}{w^T\sum_0w+w^T\sum_1w}=\frac{w^T(M_0-M_1)(M_0-M_1)^Tw}{w^T(\sum_0+\sum_1)w}}$
定义“类内散度矩阵”(有时间再敲公式)

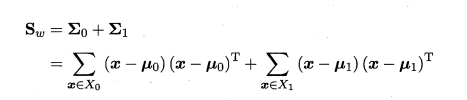
以及“类间散度矩阵”

则上式可以写作：

${J=\frac{w^TS_bw}{w^TS_ww}}$
可以注意到上式中的有关于W长度的项可以消去，故该解只与其方向有关，最终可以解出
${w=S^{-1}_w(M_0-M_1)}$
若将LDA推广到多分类问题中，则可以同理定义一个“**全局散度矩阵**”同理进行求解。

3.5 多分类学习

多分类学习的基本思路是将多分类任务拆为若干个二分类任务进行求解（类似于折半）

关键问题：如何对多分类任务进行拆分，如何对多个分类器进行集成。

拆分策略

• OvO：将类别两两配对，从而产生N(N-1)/2个二分类任务，将被预测得最多的类别作为最终分类结果
• OvR：每次将一个类的样例作为正例其他类的样例作为反例训练N个分类器。测试时若仅有一个分类器预测为正类，则对应的类别标记作为最终分类结果；若有多个分类器预测为正类，则选择置信度最大的类别标记作为分类结果。
• MvM：每次将若干类作为正类，若干类作为范雷，通常使用纠错输出码来对正反类构造进行特殊的设计

3.6 类别不平衡问题

处理类别不平衡学习的一个基本策略——“再缩放”

实际操作的三种方法：

• 欠采样：去除反例使二者数量相当
• 过采样：增加正例使二者数量相当（增加部分不应与原始有过大重叠
• 阈值移动：基于原始训练集进行学习
  
  
  
  家人们晚安(￣o￣) . z Z