「SOL」序列 (LOJ/NOI2019)

准备写新博客的时候发现自己草稿箱里还有一篇咕了十几天的题解

思路挂在了费用流之前……

题面

解析

这道题的本质是一个二分图带权匹配的问题，一个经典的做法是直接做费用流。

考虑如何在流网络中体现限制。只能选择恰好 $K$ 对非常简单，只需要控制总流量为 $K$ 即可；主要是 $L$ 的限制。网络流并不容易限制下界，所幸总流量固定为 $K$，所以反过来考虑，「至少有 $L$ 对 “A-A” 型的匹配」，则「至多有 $K-L$ 对 “A-B” 型的匹配」。

考虑这样建图（以下「边权」指边的费用）：

$a,b$ 两个序列各自作为二分图的一个部，$a$ 部与源点 $S$ 的边权为 $a_i$，$b$ 部与汇点同理；
$a_i$ 到 $b_i$ 直接连边，表示一种 “A-A” 型的匹配；
新建两个特殊点 $p,q$，边 $p\to q$ 容量限制为 $K-L$，用于处理 “A-B” 型：
- $a_i$ 向 $p$ 连边，$q$ 向 $b_j$ 连边；
- 这样 $a_i\to p\to q\to b_j$ 即构成了 “A-B” 型匹配。

流网络大概长这样：

直接限制总流量为 $K$ 跑最大费用流，可以获得不错的部分分。

既然是费用流，而且流网络比较规整，可以尝试模拟费用流 —— 简单的说就是快速找“$S$ 到 $T$ 的最长路”。考虑一条最长路会长什么样。

一个点「被选」指它的匹配方式是 A-B 匹配，一个 S 部的被选点 $u$ 具有反向边 $p\to u$，一个 T 部的被选点 $v$ 具有反向边 $v\to q$。

一个点「为空」指它还没有被匹配。

一条路径开头一定是 $S\to a$，结尾一定是 $b'\to T$，其中 $a,b'$ 均为空。大概会有以下四种情况：

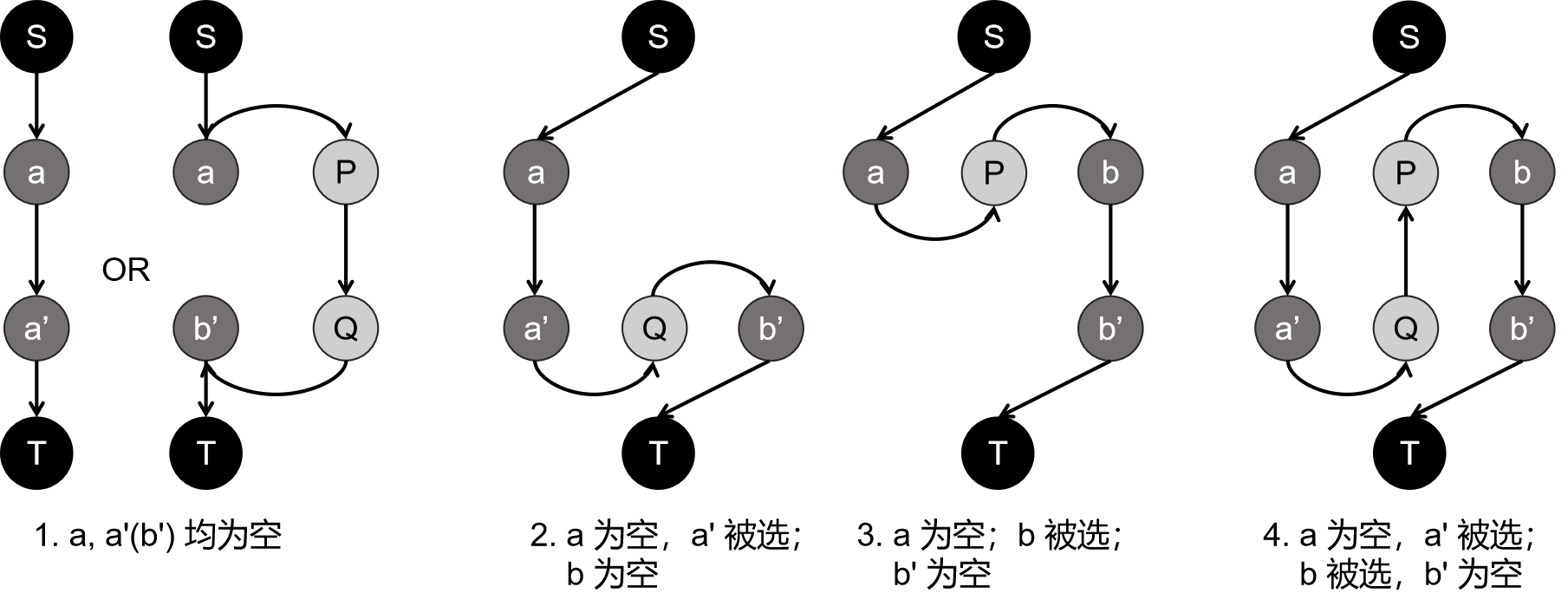
注意到只有 $S\to a$ 和 $b'\to T$ 这两种边有费用，所以决定路径长度的其实就只有开头和结尾。

于是我们发现我们需要维护以下信息：

空的 $a$；
空的 $b'$；
$a'$ 被选，且 $a$ 为空的 $a$；
$b$ 被选，且 $b'$ 为空的 $b'$；

这四类信息都可以用堆维护最大值。继续考虑如何模拟费用流——

我们每找一条最长路，就会把 $S\to T$ 的总流量增加 $1$，所以限制总流量为 $K$ 则只需要找 $K$ 次最长路即可。

然后这张流网络上还有一条特殊的边 $P\to Q$，需要维护它的容量。在上图列出的四种情况中：

若为 $a\to a'$，则容量不变；若为 $a\to b'$，则容量 $-1$；
容量不变；
容量不变；
容量 $+1$。

另外，我们有时会发现 $a$ 和 $a'$ 同时被选，显然是不优的。这种时候就可以把 $a$ 和 $a'$ 同时改为不被选，答案不变但是 $P\to Q$ 容量 $+1$。

直接模拟即可。

源代码

/*Lucky_Glass*/

#include <queue>

#include <cstdio>

#include <cstring>

#include <cassert>

#include <algorithm>

inline int rin(int &r) {

  int c = getchar(); r = 0;

  while ( c < '0' || '9' < c ) c = getchar();

  while ( '0' <= c && c <= '9' ) r = r * 10 + (c ^ '0'), c = getchar();

  return r;

}

typedef long long llong;

typedef std::pair<int, int> pii;

#define CON(typ) const typ &

const int N = 2e5 + 10;

int ncas, n, nk, nl;

int num[N << 1];

std::priority_queue<pii> emp[2], opp[2], par;

bool cov[N << 1], used[N << 1];

void clean() {

  while ( !emp[0].empty() ) emp[0].pop();

  while ( !emp[1].empty() ) emp[1].pop();

  while ( !opp[0].empty() ) opp[0].pop();

  while ( !opp[1].empty() ) opp[1].pop();

  while ( !par.empty() ) par.pop();

  for ( int i = 1; i <= (n << 1); ++i )

    cov[i] = used[i] = false;

}

int empTop(CON(bool) typ) {

  while ( !emp[typ].empty() && used[emp[typ].top().second] ) emp[typ].pop();

  return emp[typ].empty() ? -1 : emp[typ].top().second;

}

int oppTop(CON(bool) typ) {

#define OPPID(x) ((x) <= n ? (x) + n : (x) - n)

  while ( !opp[typ].empty() && (used[opp[typ].top().second]

         || !cov[OPPID(opp[typ].top().second)]) )

    opp[typ].pop();

  return opp[typ].empty() ? -1 : opp[typ].top().second;

#undef OPPID

}

int parTop() {

  while ( !par.empty() && (used[par.top().second]

         || used[par.top().second + n]) )

    par.pop();

  return par.empty() ? -1 : par.top().second;

}

void checkCross(CON(int) id, int &rem) {

#define OPPID(x) ((x) <= n ? (x) + n : (x) - n)

  if ( cov[OPPID(id)] && cov[id] ) {

    cov[OPPID(id)] = cov[id] = false;

    ++rem;

  }

#undef OPPID

}

llong findPath(int &rem) {

#define GID(x) (std::make_pair(num[x], x))

  llong ee = -1, eo = -1, oe = -1, oo = -1;

  int etop[2] = {empTop(0), empTop(1)}, otop[2] = {oppTop(0), oppTop(1)},

      ptop = parTop();

  if ( rem && ~etop[0] && ~etop[1] ) ee = num[etop[0]] + num[etop[1]];

  if ( !rem && ~ptop ) ee = num[ptop] + num[ptop + n];

  if ( ~etop[0] && ~otop[1] ) eo = num[etop[0]] + num[otop[1]];

  if ( ~otop[0] && ~etop[1] ) oe = num[otop[0]] + num[etop[1]];

  if ( ~otop[0] && ~otop[1] ) oo = num[otop[0]] + num[otop[1]];

  llong mx = std::max(std::max(ee, eo), std::max(oe, oo));

  if ( mx == ee ) {

    if ( rem ) {

      --rem;

      used[etop[0]] = used[etop[1]] = true;

      cov[etop[0]] = cov[etop[1]] = true;

      checkCross(etop[0], rem), checkCross(etop[1], rem);

      opp[1].push(GID(etop[0] + n));

      opp[0].push(GID(etop[1] - n));

    }

    else {

      used[ptop] = used[ptop + n] = true;

    }

  } else if ( mx == eo ) {

    used[etop[0]] = used[otop[1]] = true;

    cov[etop[0]] = true, cov[otop[1] - n] = false;

    checkCross(etop[0], rem);

    opp[1].push(GID(etop[0] + n));

  } else if ( mx == oe ) {

    used[otop[0]] = used[etop[1]] = true;

    cov[etop[1]] = true, cov[otop[0] + n] = false;

    checkCross(etop[1], rem);

    opp[0].push(GID(etop[1] - n));

  } else {

    ++rem;

    used[otop[0]] = used[otop[1]] = true;

    cov[otop[0] + n] = cov[otop[1] - n] = false;

  }

  return mx;

}

void solve() {

  rin(n), rin(nk), rin(nl);

  clean();

  for ( int i = 1; i <= n; ++i )

    emp[0].push(std::make_pair(rin(num[i]), i));

  for ( int i = 1; i <= n; ++i ) {

    emp[1].push(std::make_pair(rin(num[i + n]), i + n));

    par.push(std::make_pair(num[i] + num[i + n], i));

  }

  llong ans = 0;

  int rem = nk - nl;

  for ( int i = 0; i < nk; ++i )

    ans += findPath(rem);

  printf("%lld\n", ans);

}

int main() {

  freopen("sequence.in", "r", stdin);

  freopen("sequence.out", "w", stdout);

  rin(ncas);

  while ( ncas-- ) solve();

  return 0;

}

THE END

Thanks for reading!

若写花开花落花飞花舞太遥远

若写风去风回风追风止太疲倦

若写日升月落斗转星移太幽怨

写你看我一颦一笑太腼腆

——《词不达意》 By 夏语遥

> Link 词不达意 - 网易云