几种排序（c#实现）

　　代码：

            int[] arr = { 2, 3, 4, 6, 1, 5, 4 };
            // 冒泡排序：把最小的往前冒 O(n2)
            //int temp1;
            //for (int i = 0; i < arr.Length - 1; i++)
            //{
            //    for (int j = i + 1; j < arr.Length; j++)
            //    {
            //        if (arr[j] < arr[i])
            //        {
            //            temp1 = arr[j];
            //            arr[j] = arr[i];
            //            arr[i] = temp1;
            //        }
            //    }
            //}
            // 选择排序：从小到大依次选出来 O(n2)
            //for (int i = 0; i < arr.Length - 1; i++)
            //{
            //    int temp2 = arr[i];
            //    int index = i;
            //    for (int j = i + 1; j < arr.Length; j++)
            //    {
            //        if (arr[j] < temp2)
            //        {
            //            temp2 = arr[j];
            //            index = j;
            //        }
            //    }
            //    arr[index] = arr[i];
            //    arr[i] = temp2;
            //}
            // 直接插入排序：适合基本有序 O(n2)
            //for (int i = 1; i < arr.Length; i++)
            //{
            //    int temp = arr[i];
            //    int j;
            //    for (j = i - 1; j >= 0; j--)
            //    {
            //        if (temp > arr[j])
            //        {
            //            break;
            //        }
            //        arr[j + 1] = arr[j];
            //    }
            //    arr[j + 1] = temp;
            //}
            // 希尔排序
            //int gap = arr.Length / 2;
            //while (gap >= 1)
            //{
            //    // 把距离为 gap 的元素编为一个组，扫描所有组
            //    for (int i = gap; i < arr.Length; i++)
            //    {
            //        int j = 0;
            //        int temp = arr[i];
            //        // 对距离为 gap 的元素组进行排序
            //        for (j = i - gap; j >= 0 && temp < arr[j]; j = j - gap)
            //        {
            //            arr[j + gap] = arr[j];
            //        }
            //        arr[j + gap] = temp;
            //    }
            //    gap = gap / 2;
            //}

            for (int i = 0; i < arr.Length; i++)
            {
                Console.WriteLine(arr[i]);
            }
            Console.ReadLine();

二、程序员内功修炼（排序）

1、直接插入排序：适合数组基本有序的情况

　　像打扑克牌，从前往后对应，把数字插入到合适的位置，如：

　　

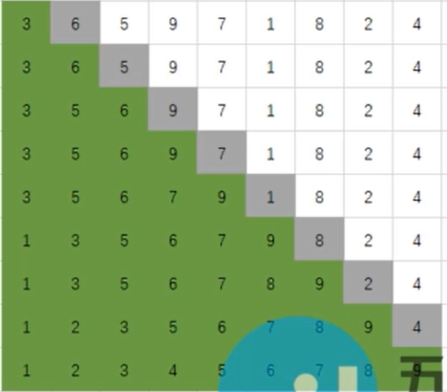
　　初始值3，认为一个已经有序的序列

　　第一次遍历：6和3比

　　第二次遍历：5和6、5和3

　　第三次遍历：9和6

　　弟四次遍历：7和9、7和6

　　以此类推。。

　　代码：

        public static int[] InsertionSort(int[] arr)
        {
            /*
             数据结构-数组
             最差时间复杂度-输入的序列为降序，复杂度为O(n^2)
             最优时间复杂度-输入的序列为升序，复杂度为O(n)
             辅助空间-O(1)
             稳定性-稳定
             */
            for (int i = 1; i < arr.Length; i++)
            {
                int temp = arr[i];
                int j = i - 1;
                while (j >= 0 && temp < arr[j])
                {
                    arr[j + 1] = arr[j];
                    j--;
                }
                arr[j + 1] = temp;
            }
            return arr;
        }

2、二分插入排序（是对直接插入排序的改进）：适合数组较长的情况

　　直接插入排序每次遍历均是从右往左找，直到找到比自己小的，当序列足够长的情况下，这很耗时

　　二分是取前面有序序列的中间值做对比，一半一半缩小范围，减少排序对比时间。

        public static int[] BinarySort(int[] arr)
        {
            /*
            数据结构-数组
            最差时间复杂度-输入的序列为降序，复杂度为O(n^2)
            最优时间复杂度-输入的序列为升序，复杂度为O(log2 n)
            辅助空间-O(1)
            稳定性-稳定
            */
            for (int i = 1; i < arr.Length; i++)
            {
                int temp = arr[i];
                int low = 0;
                int high = i - 1;
                while (low <= high)
                {
                    int mid = (low + high) / 2;
                    if (temp >= arr[mid])
                        low = mid + 1;
                    else
                        high = mid - 1;
                }
                for (int j = i - 1; j >= low; j--)
                {
                    arr[j + 1] = arr[j];
                }
                arr[low] = temp;
            }
            return arr;
        }

3、希尔排序

　　又称为缩小增量排序，定义排序间隔，并逐步缩小增量，如图：

　　

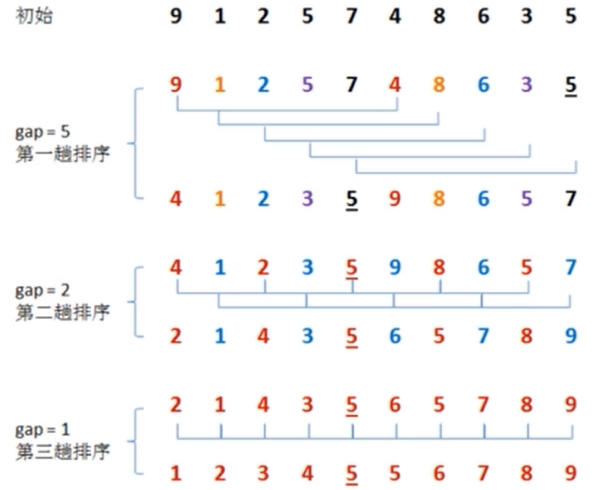
        public static int[] ShellSort(int[] arr)
        {
            /*
            数据结构-数组
            最差时间复杂度-根据步长的不同而不同，已知最好的为O(n(log2 n)^2)
            最优时间复杂度-O(n)
            辅助空间-O(1)
            稳定性-不稳定
            */
            for (int gap = arr.Length / 2; gap >= 1; gap = gap / 2)
            {
                for (int i = gap; i < arr.Length; i++)
                {
                    int temp = arr[i];
                    int j = i - gap;
                    while (j >= 0 && temp < arr[j])
                    {
                        arr[j + gap] = arr[j];
                        j = j - gap;
                    }
                    arr[j + gap] = temp;
                }
            }
            return arr;
        }

4、冒泡排序

　　最小的往前冒  或者  最大的往后冒

        public static int[] BubbleSort(int[] arr)
        {
            /*
            数据结构-数组
            最差时间复杂度-O(n^2)
            最优时间复杂度-O(n^2)
            辅助空间-O(1)
            稳定性-稳定
            */
            for (int i = 0; i < arr.Length - 1; i++)
            {
                for (int j = i + 1; j < arr.Length; j++)
                {
                    if (arr[j] < arr[i])
                    {
                        int temp = arr[j];
                        arr[j] = arr[i];
                        arr[i] = temp;
                    }
                }
            }
            return arr;
        }

5、快速排序（目前最好的排序）

　　以第一个元素为基准值，把剩余元素小的放前边，大的放后边

　　

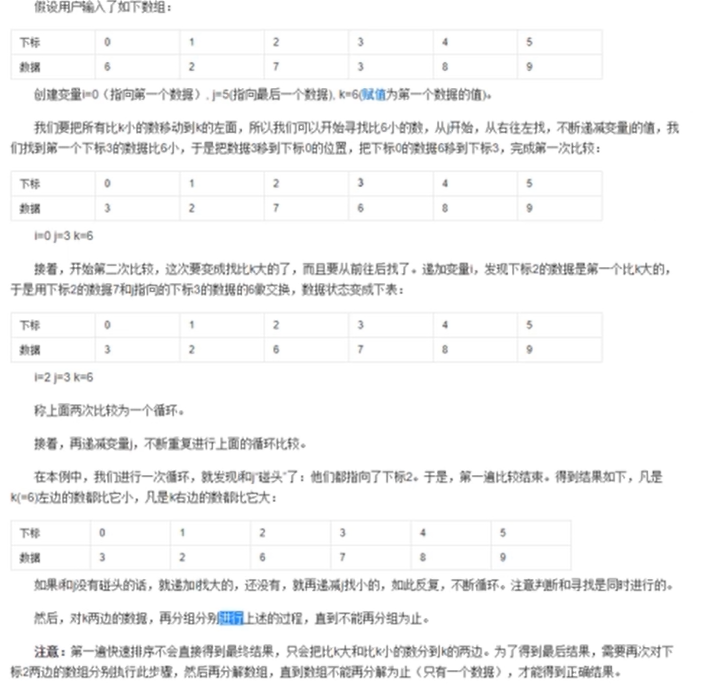
        public static int[] QuickSort(int[] arr, int low, int high)
        {
            /*
            数据结构-数组
            最差时间复杂度-每次选取的基准值都是最大或者最小O(n^2)
            最优时间复杂度-每次选取的基准值都是中位数O(nlogn)
            辅助空间-主要是递归造成的栈空间的使用，取决于递归树的深度，一般为O(logn)，最差为O(n)
            稳定性-不稳定
            */
            if (low >= high)
                return arr;
            int i = low;
            int j = high;
            int temp = arr[i];//基准值
            while (i < j)//从两端向中间扫描,跳出循环时i=j
            {
                while (i < j && arr[j] >= temp)//从右往左
                    j--;
                arr[i] = arr[j];
                while (i < j && arr[i] <= temp)//从左往右
                    i++;
                arr[j] = arr[i];
            }
            arr[i] = temp;// 基准值回归正确位置
            QuickSort(arr, low, i - 1);
            QuickSort(arr, i + 1, high);
            return arr;
        }

6、直接选择排序

　　直接选择最小的，和第一位替换位置，以此类推

        public static int[] SelectionSort(int[] arr)
        {
            /*
            数据结构-数组
            最差时间复杂度-O(n^2)
            最优时间复杂度-O(n^2)
            辅助空间-O(1)
            稳定性-不稳定
            */
            for (int i = 0; i < arr.Length - 1; i++)
            {
                int k = i; // k指向最小值索引
                for (int j = i + 1; j < arr.Length; j++)
                    if (arr[j] < arr[k])
                        k = j;
                if (k != i)
                {
                    int temp = arr[i];
                    arr[i] = arr[k];
                    arr[k] = temp;
                }
            }
            return arr;
        }