R数据分析：纵向分类结局的分析-马尔可夫多态模型的理解与实操

今天要给大家分享的统计方法是马尔可夫多态模型，思路来源是下面这篇文章：

Ward DD, Wallace LMK, Rockwood K

Cumulative health deficits, APOE genotype, and risk for later-life mild cognitive impairment and dementia

Journal of Neurology, Neurosurgery & Psychiatry 2021;92:136-142.

我们知道轻度认知损害随着时间的发展有可能会发展成痴呆，也可能会恢复，有可能不变，那这篇文章要解决的问题就是找到引起人群不同认知状态变化的风险因子，因子其实有很多啦，作者本文只关注一个，叫做年龄相关的健康赤字（age-related health deficits）。作者想探讨年龄相关的健康赤字是如何对认知状态的转换起作用的。

作者用了马尔可夫多态模型Markov multi-state models回答了自己的研究问题，相应地，如果你的感兴趣的结局变量是分类变量，比如状态，并且各种状态之间可以相互转换，你想看看到底哪些因素影响了某种转化的风险，那么今天介绍的马尔可夫多态模型就值得你好好研究下了。

多态马尔可夫模型

要理解多态马尔可夫模型multistate Markov models，首先要知道马尔可夫过程（Markov process）

马尔可夫过程（Markov process）是一类随机过程，因为是俄国数学家A.A.马尔可夫于1907年提出来的，所以有了这么个名字。该过程就是说：在已知目前状态（现在）的条件下，它未来的演变（将来）不依赖于它以往的演变 (过去 )。这种已知“现在”的条件下，“将来”与“过去”独立的特性称为马尔可夫性质，具有这种性质的随机过程叫做马尔可夫过程，最简单的马尔可夫过程就是一阶过程，每一个状态的转移只依赖于其之前的那一个状态。

假设这个模型的每个状态都只依赖于之前的状态，这个假设被称为马尔科夫假设，这个假设可以大大地简化具有马尔可夫过程的随机性问题。

现在给出马尔可夫模型的说明

The Markov models stand out as much simpler than other models from a probability point of view, and this simplifies the likelihood evaluation

可以理解为马尔可夫模型是对状态改变情况的合理的简化假设。那么我们接着看多态模型：

多态模型的基本说明如下图：

就是说多态模型是来探讨转换状态的，一个个体在观测的特定时期一定是处于确定数量状态中的一种，对于这类情况我们就可以用多态模型来研究。如果这些状态的转换如果满足马尔可夫性质，此时就叫做马尔可夫多态模型。

就是你手上恰好有纵向随访数据，结局变量是分类变量（连续变量也可以转化成有临床意义的分类变量），你好奇随着时间的变化，个体的在各个类别的转化情况是怎么样的，以及影响转化概率的因素有哪些，那么就可以考虑使用多态模型。

A multi-state model describes how an individual moves between a series of states in continuous time

经典的多态模型就是研究疾病状态转换时使用的多态马尔可夫多态模型，模型图示如下：就是一个病人疾病可以加深可以恢复，并且随时都可能死亡的多态模型，在这种模型中，下次状态的改变只和当前状态有关

in which individuals can advance or recover between adjacent disease states, or die from any state.：

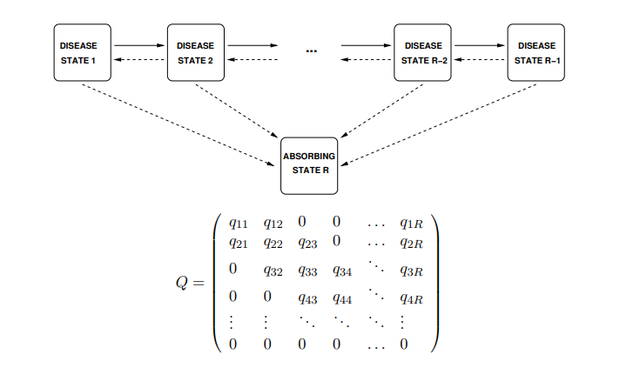
Fitting multi-state models to panel data generally relies on the Markov assumption, that future evolution only depends on the current state.

常见的操作就是使用多态Markov模型（Multi-states Markov model，MSM）利用纵向数据估计特定人群在不同时间内健康状态的转换概率，并对其健康状态的转换风险进行多因素探讨，这儿也给大家贴两篇多态马尔可夫模型的中文文献，感兴趣的同学可以自行去下载查看：

展元元, 韩耀风, 方亚. 基于多状态Markov模型的我国老年人无失能期望寿命及其影响因素. 中华流行病学杂志, 2021, 42(6): 1024-1029

石舒原, 赵厚宇, 刘志科, 杨晴晴, 沈鹏, 詹思延, 林鸿波, 孙凤. 多状态马尔科夫模型估计2型糖尿病患者慢性并发症累积数量的转移概率及影响因素研究. 中华流行病学杂志, 2021, 42(7): 1274-1279

反正我觉得这个模型对做科研的临床医生应该挺有用的吧，值得去学习的。

论文报告方法

依然是回到我们文章开头提到的文章中，文章中是有画一个状态转化的示意图的，如下：

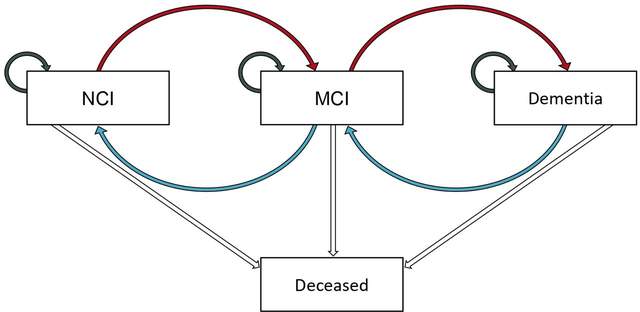
在文章中作者定义了3种状态NCI, MCI and dementia，并且认为转换过程可以向前也可以向后，并且随时可以死亡，但是转换只能在相邻两种状态之间转换而不能跳跃（当然做统计的时候这些条件都是可以自己根据客观情况设定的）。论文报告了各个状态的转换次数和相应转换方式的转换概率，如图：

就是所作者报告了各个状态转换的次数和转换概率，这个很好理解。

结合研究问题，文章最重要的结果信息就是年龄相关的健康赤字frailty index score对状态转换的影响究竟如何，作者给出了不同亚组健康赤字对不同转换的HR的森林图：

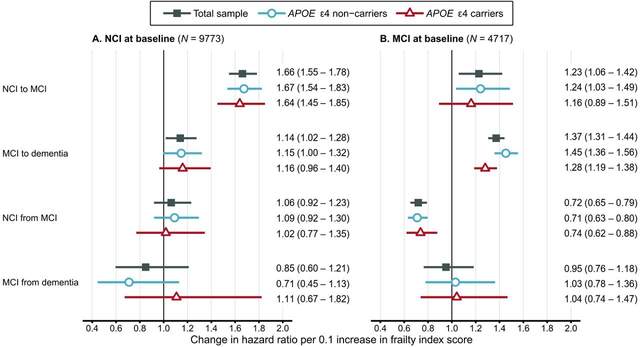
可以看到，frailty index score对每条作者关心的转换方式的HR都是有展示的，并且好多亚组的结果都呈现在了上图中，比如通过上图我们就可以知道，无论是否携带APOE，frailty index score的增长总是会使得从NCI转换成MCI,和MCI转换成痴呆的风险变高。

根据上面的结果作者就明白了年龄相关的健康赤字究竟是如何影响痴呆状态发生发展的。

上面基本上就是论文的主要分析，细枝末节大家自己去看原文哈，我们接着看操作。

实例操练

我现在手上有如下数据集：

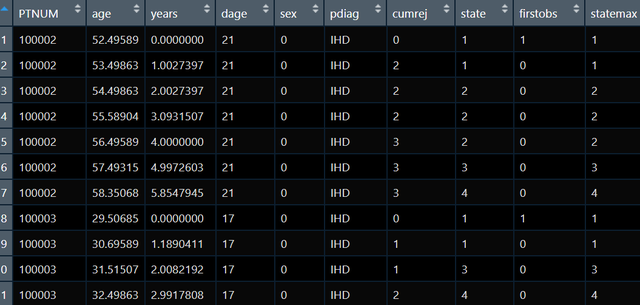
其中PTNUM是病人编号，age是每次随访的年龄，year是随访时时间，state是随访时的状态总共有4种，我现在想做马尔可夫多态模型看一下究竟是哪些因素影响了各个状态转换，在做多态模型的时候需要将同一个病人的数据放一起，并且个体内随访时间应该升序排列（就像上图一样的）：

observations from the same subject must be adjacent in the dataset, and observations must be ordered by time within subjects.

数据这么处理后我们就可以很方便地统计出状态转化次数矩阵，代码如下：

statetable.msm(state, PTNUM, data=cav)

转换次数输出结果如下：

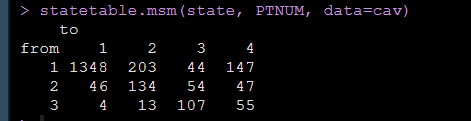
上面的结果就显示了随着随访的进行，有多少人从一个状态转化到了另外一个状态，就是论文中报告的每个转化的转化次数，我们还可以使用pmatrix.msm函数得到转化概率矩阵，如下图：

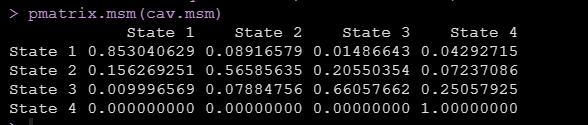
有了状态转换次数和状态转换概率，论文中的table2就出来了。

再继续探讨状态转换的影响因素，在探究状态转化影响因素之前，我们需要设定一个转化的限制矩阵，比如论文中的状态转化情况就可以用如下矩阵表示：

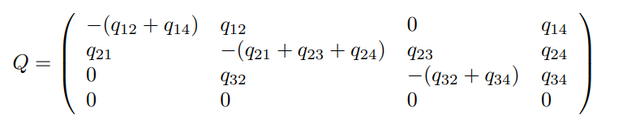
就是说我可以从状态1NCI转换到状态2MCI，也可以从MCI转回NCI，每一种状态也都可以转成状态4死亡，但是也不能跨状态转换，而且死亡之后也不可能转换成状态1，2，3。那么相应的不可转换的情况在矩阵中都要固定为0。

状态转换的情况我们根据实际设定好之后我们就可以运行多态模型了,代码如下：

msm_model <- msm(state ~ years, subject = PTNUM, data = mydata,
                    covariates = ~ dage + ihd,
                    qmatrix = twoway4.q,
                    death = 4,
                    method = "BFGS", control = list(fnscale = 4000, maxit = 10000))

代码运行的过程就是就是去寻找最符合我们数据maximise the likelihood的同时又满足我们设定的转换参数的过程。

运行上面的代码即可得到相应影响因素的HR和置信区间，比如两个协变量dage和ihd对各个状态转化情况的HR如下：

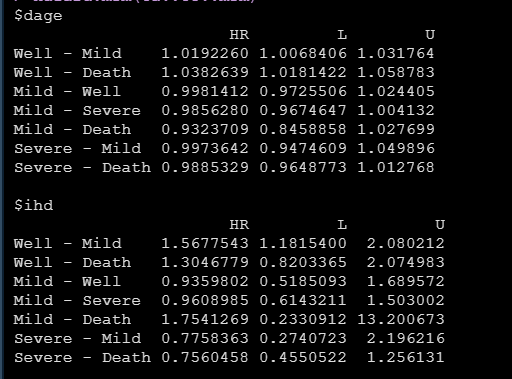
后面的工作就是根据各个亚组的HR和置信区间将森林图做出来，然后对标论文就算完成啦。今天的分享就到这儿。

小结

今天给大家写了马尔可夫多态模型的原理的做法，希望能给到大家一些思路上的启发，感谢大家耐心看完，自己的文章都写的很细，重要代码都在原文中，希望大家都可以自己做一做，请转发本文到朋友圈后私信回复“数据链接”获取所有数据和本人收集的学习资料。如果对您有用请先记得收藏，再点赞分享。

也欢迎大家的意见和建议，大家想了解什么统计方法都可以在文章下留言，说不定我看见了就会给你写教程哦，有疑问欢迎私信，有合作意向请直接滴滴我。