反馈电路的Bode分析法

1 前言

　　在反馈电路的分析中，如果前向放大倍数为A_open，反馈系数为β，则闭环传递函数A_close=A_open/(1+A_openβ)，其中A_openβ为环路增益。但是，在A_open和β的计算中均要考虑负载效应，即反馈网络会成为前馈放大器的负载，前馈放大器也会成为反馈电路的负载。负载效应会使A_open和β的计算变得复杂。另外，在计算环路增益时，也要特别考虑应该在何处断开反馈，使环路增益的计算更加准确。

　　本文介绍一种不需要断开反馈环路的反馈分析方法——Bode 分析法。此方法由H. W. Bode 在他的书Network Analysis and Feedback Amplifier Design 中提出。

　　首先，我们观察这样一件事情。在前馈放大器中肯定会有晶体管存在，也许在反馈网络中也有晶体管（也有可能没有），如果将其中一个晶体管的小信号模型重点画出，则其构成的反馈电路如图1所示。在图1中，反馈电路被建模为一个二端口网络，其中的压控电流源就是其中的一个晶体管。由于小信号模型是线性模型，因此v_out与v_in的关系可以写为v_out=A_v,closev_in，其中A_v,close为闭环电压增益。

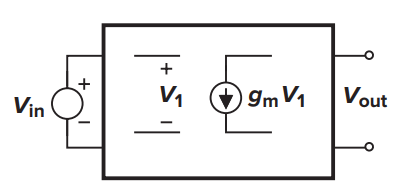
图1 反馈电路的二端口模型

2 Bode分析法

　　如果将晶体管的模型进行修改，将受控源修改为独立源，则其构成的反馈电路如图2所示。此时，电路中的激励除了v_in之外还有i₁，因此有

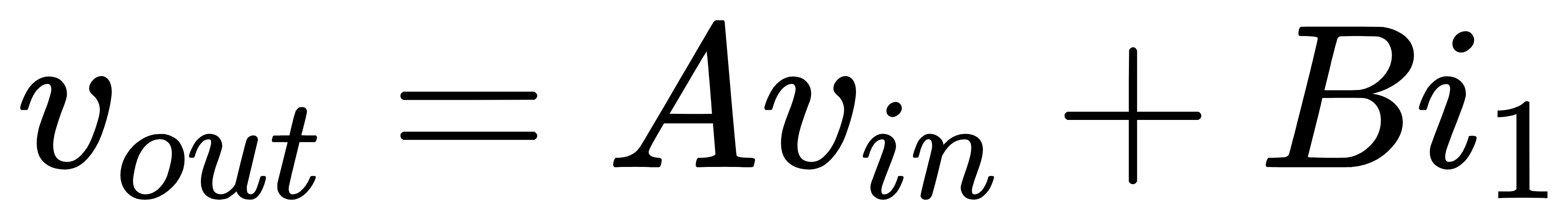
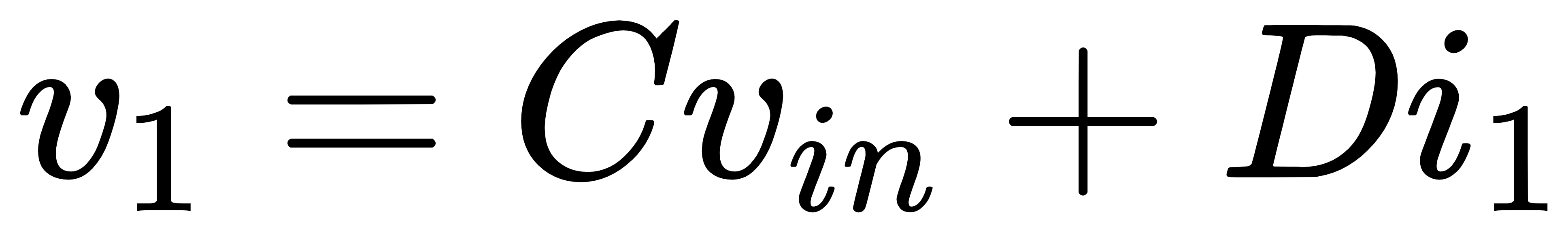
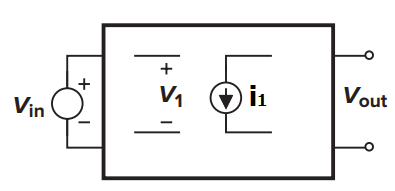
图2 将晶体管模型替换为独立源后的反馈电路二端口模型

其中，系数A、B、C和D可以由下面四个式子算出：

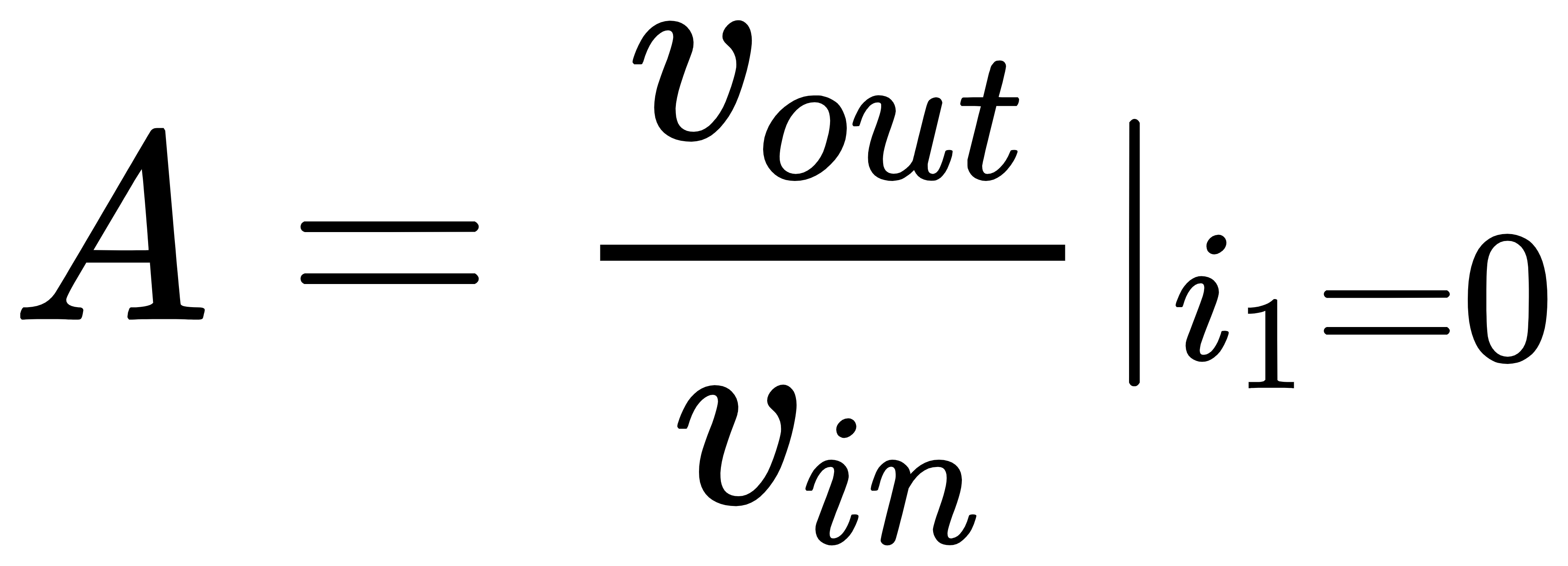
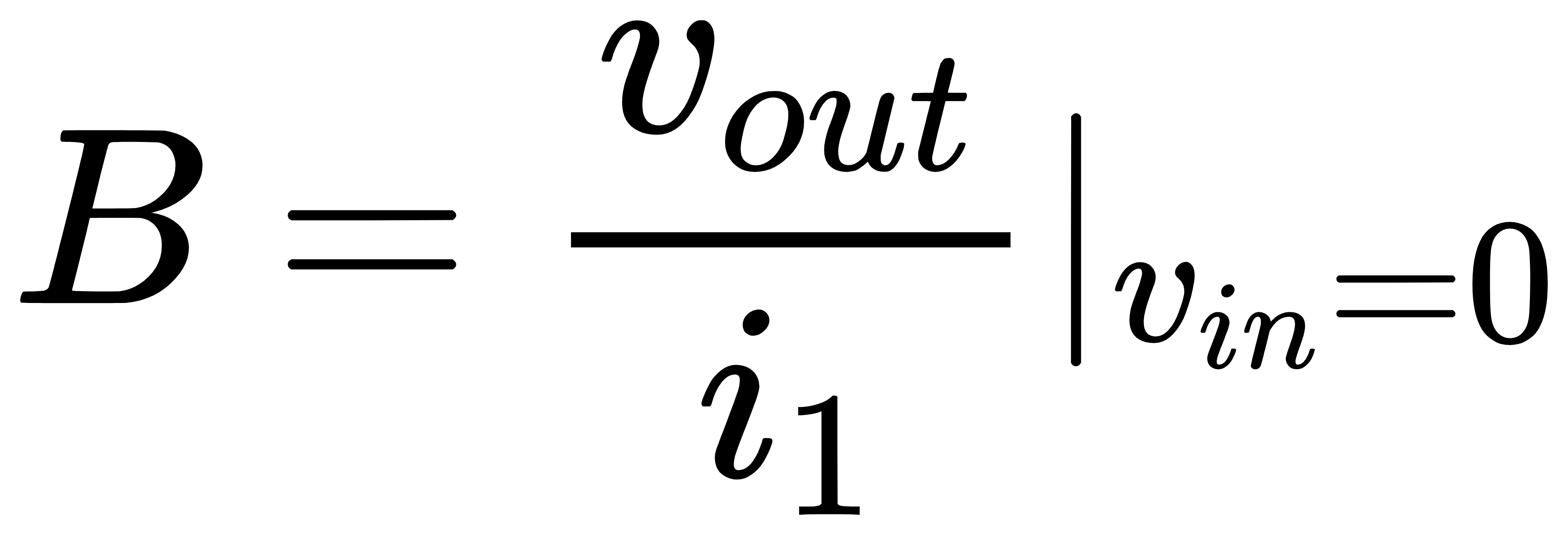
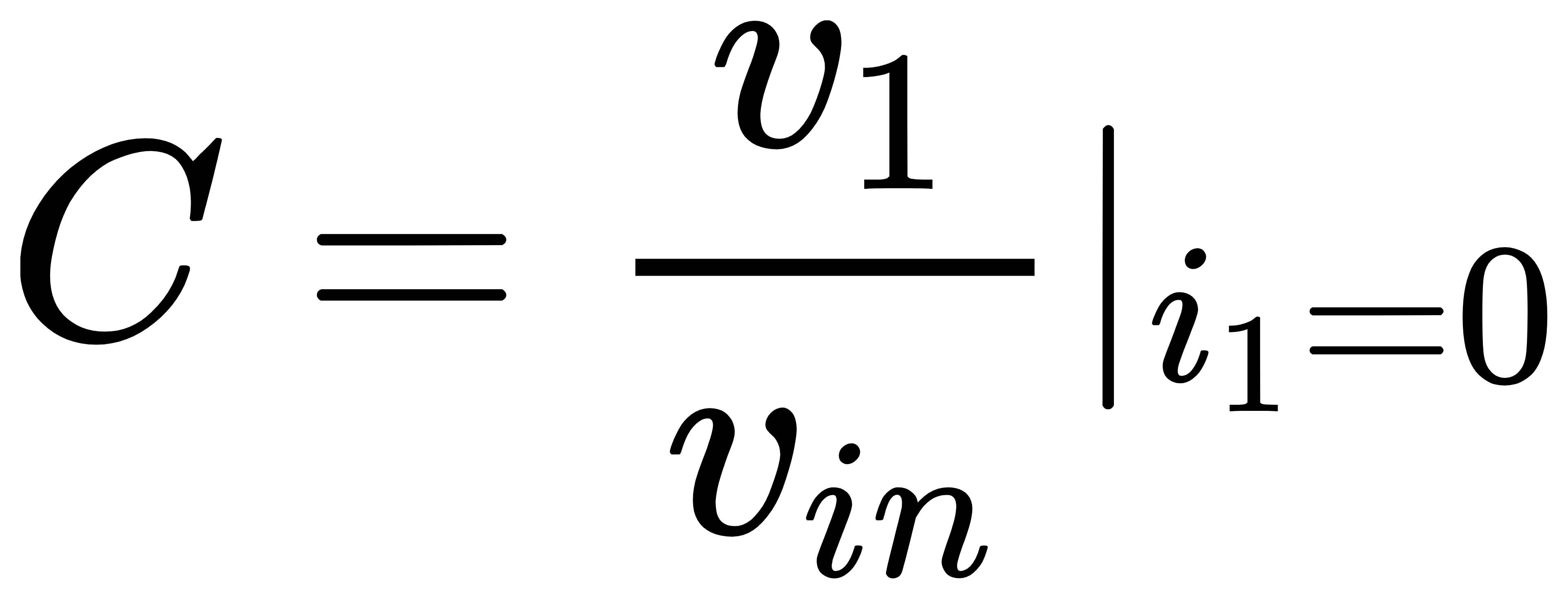
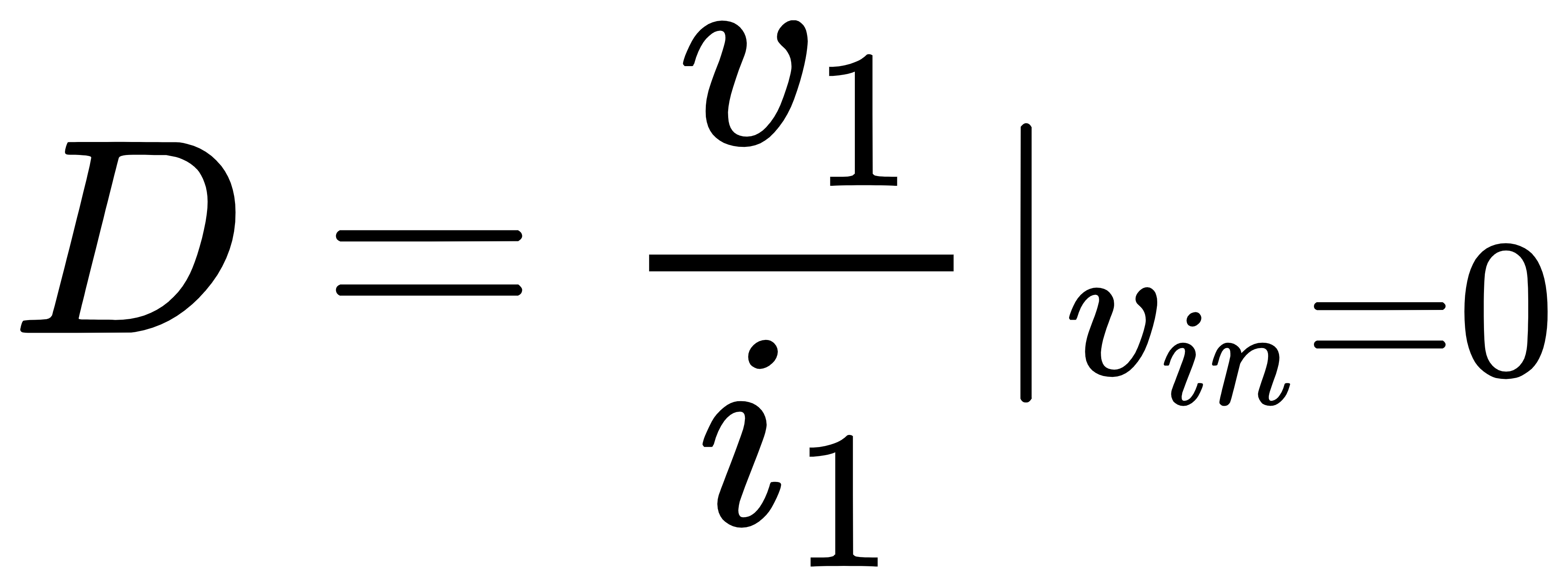
从上面的四个式子可以看出，系数A和C是在将晶体管电流强制置零时计算得出的，系数B和D是在输入置零时得出的。进一步分析可以得出，系数A代表电路的直接馈通增益，因为它是在将晶体管撤销后的电路增益，这个增益主要是由于反馈网络的直接馈通效应所引入的；系数D与该晶体管的返回比（return ratio）有关，因为它是输入为0情况下晶体管栅源电压v₁与电流i₁的比值，如果将v₁乘上晶体管的跨导g_m，则g_mv₁这个量代表栅源电压v₁应当使晶体管产生多大的漏源电流，犹如i₁经过反馈环路一圈后在原位置处又产生的电流大小，因此−g_mv₁/i₁=–g_mD可以理解为是“环路增益”（–g_mD=环路增益是有条件的，稍后会通过例子说明），更准确的说法是该晶体管的return ratio。

　　实际上i₁并不是独立源，而是受控源，其大小为i₁=g_mv₁。将i₁=g_mv₁代入v_out=Av_in+Bi₁和v₁=Cv_in+Di₁，可以得到闭环增益的表达式

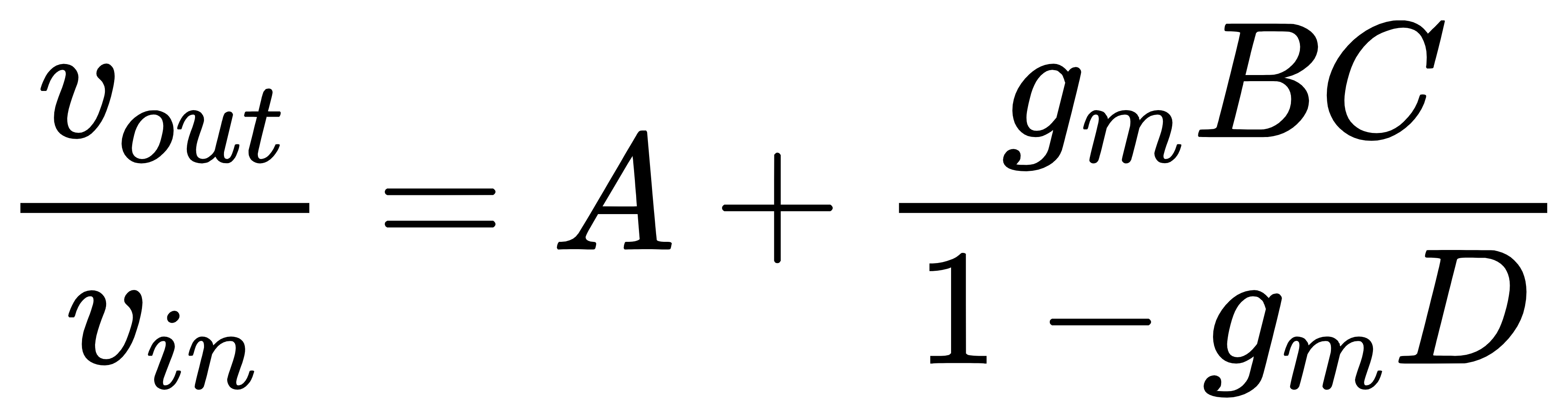
上式即为使用Bode分析法得出的闭环增益公式。我们观察上式可以得出如下结论：

（1）当g_m=0时（g_m=0代表将该晶体管撤掉），v_out/v_in=A。这更加直观地说明了系数A代表电路的直接馈通增益。

（2）如果A=0，则v_out/v_in=g_mBC/(1–g_mD)，这个表达式十分类似于通过传统的反馈分析方法得出的闭环增益表达式v_out/v_in=A_open/(1+loop gain)。事实上，如果电路中只存在一种反馈机制，并且我们所选择的晶体管处于反馈环路中，则g_mBC就是开环增益，–g_mD就是环路增益。另外，闭环增益表达式v_out/v_in=A_open/(1+loop gain)实际上忽略了反馈网络的前馈效应，即忽略了系数A。

---

例1.利用Bode分析法计算图3所示电路的闭环电压增益（1种反馈机制，M2在反馈环路中，M1不参与反馈）

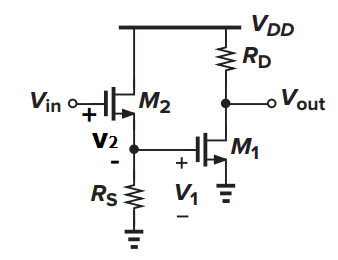
图3

　　该电路为两级放大结构，第一级为source follower，第二级为CS stage。第一级的电阻R_S引入了电流-电压反馈，M2在该反馈环路中，而M1在反馈环路外。我们首先选择晶体管M1进行分析。将M1的小信号电流i₁置零，电阻R_D上的电流为0，因此v_out=0，系数A为

借助source follower的增益公式，可以得到

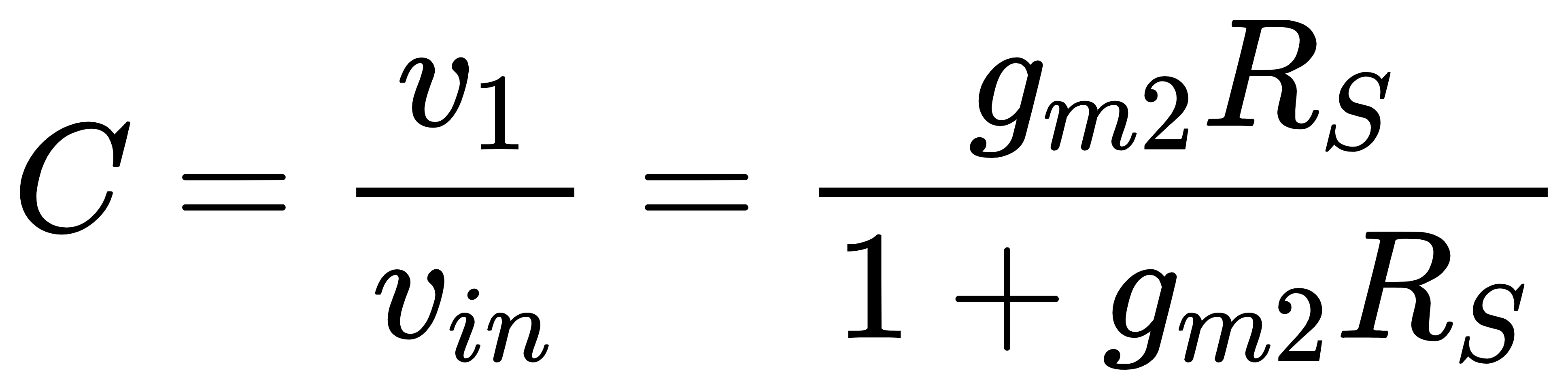
将v_in置零，可以得到

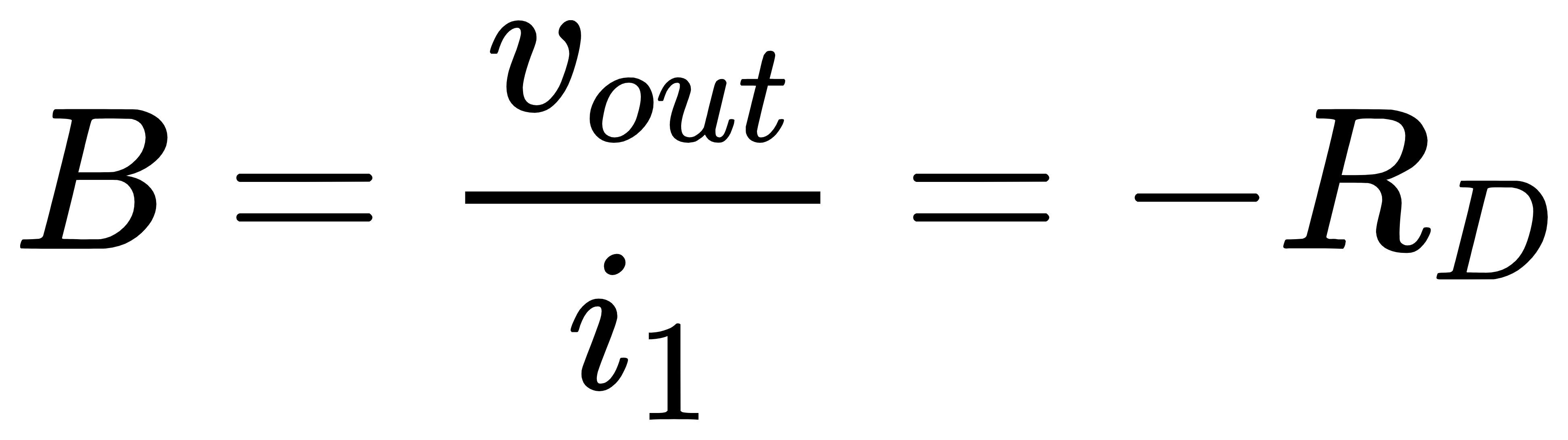
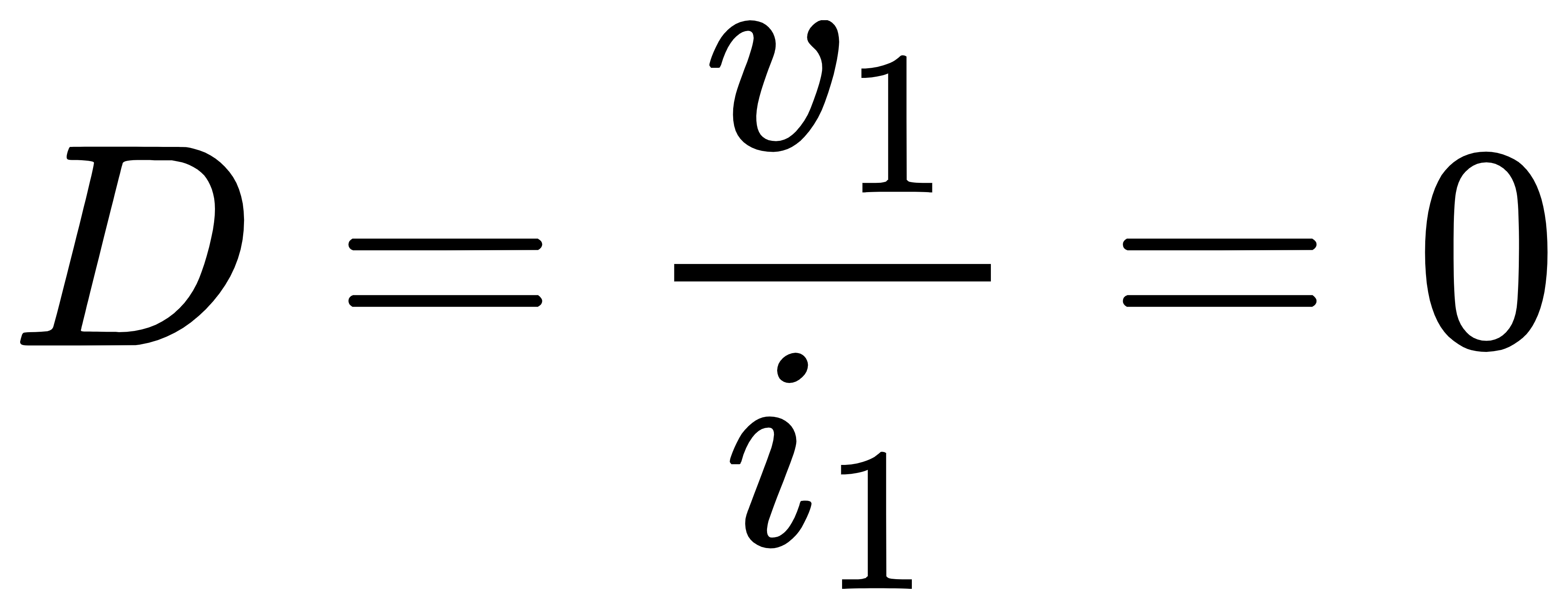
另外，M1的return ratio为

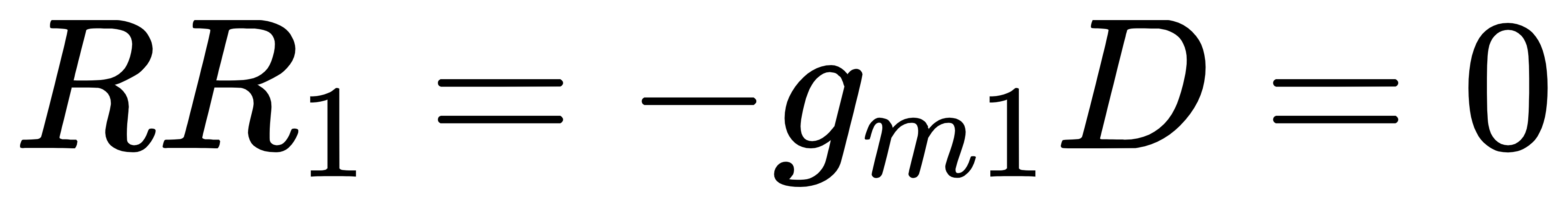
闭环电压增益

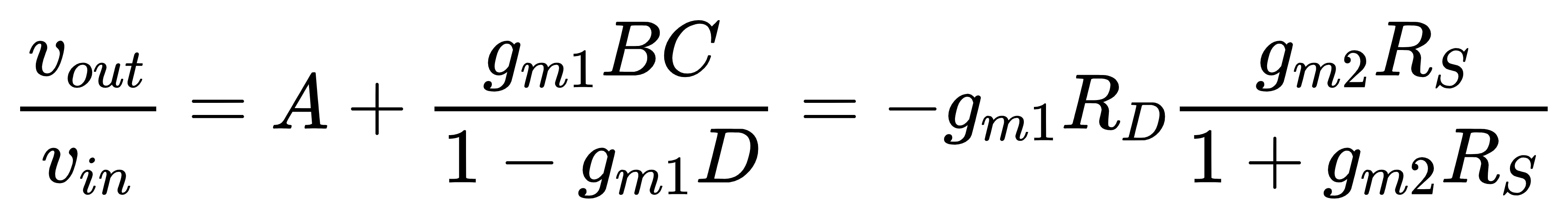
　　如果选择晶体管M2进行分析，则M2的电流i₂置零时，流经R_S的电流为0，因此v₁=0，i_d1=0，v_out=0，则有

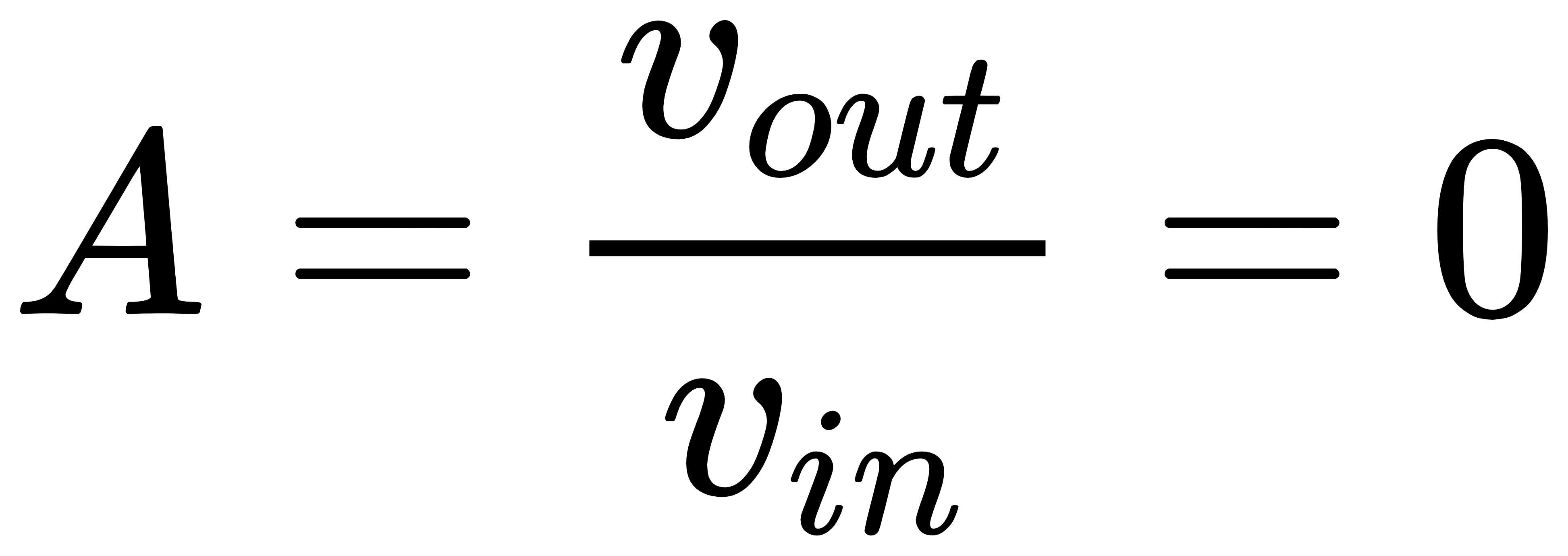
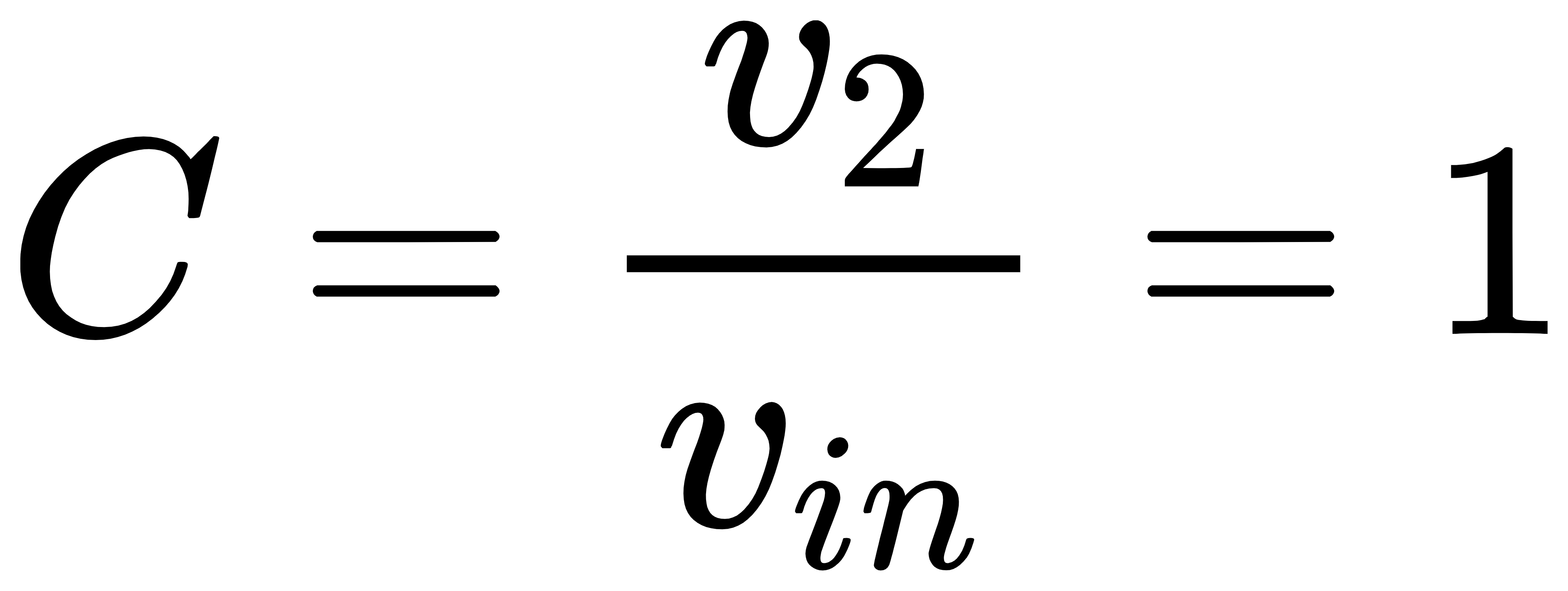
当v_in置零时，有

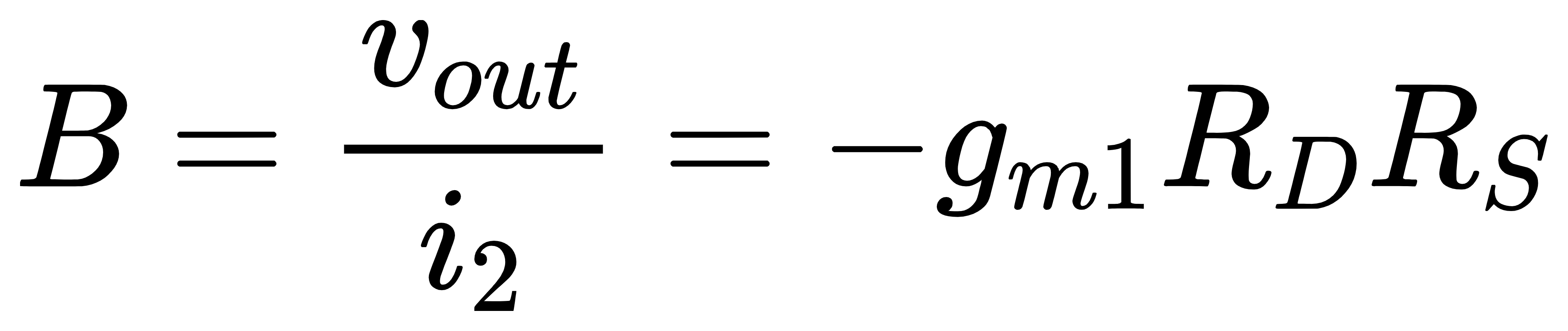
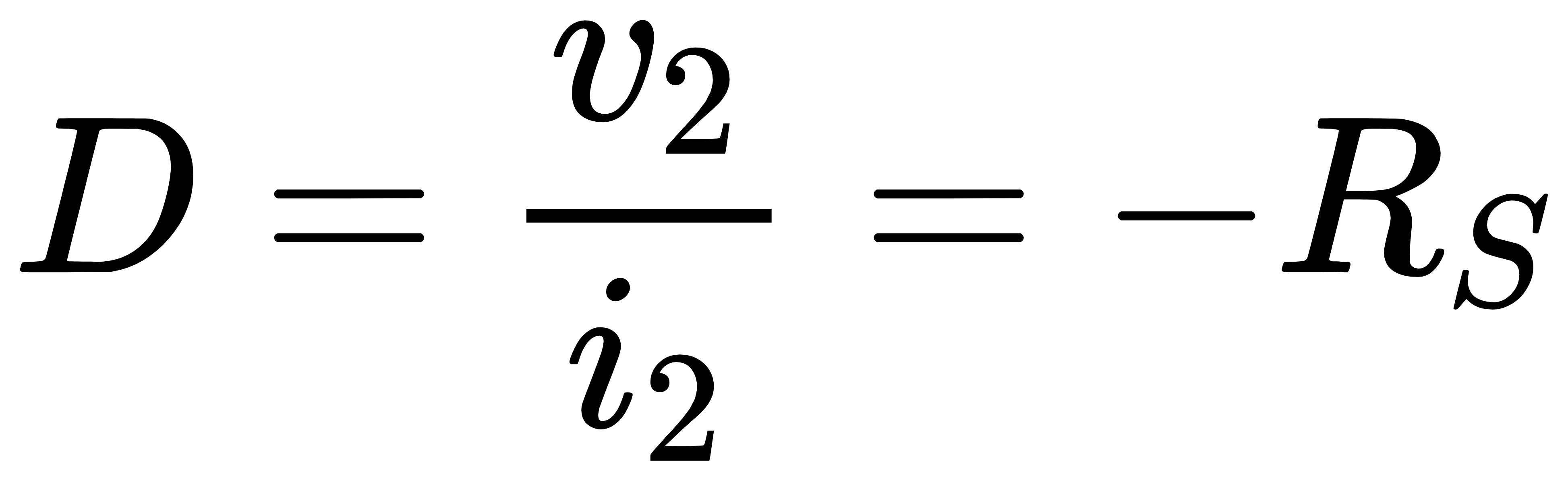
M2的return ratio为

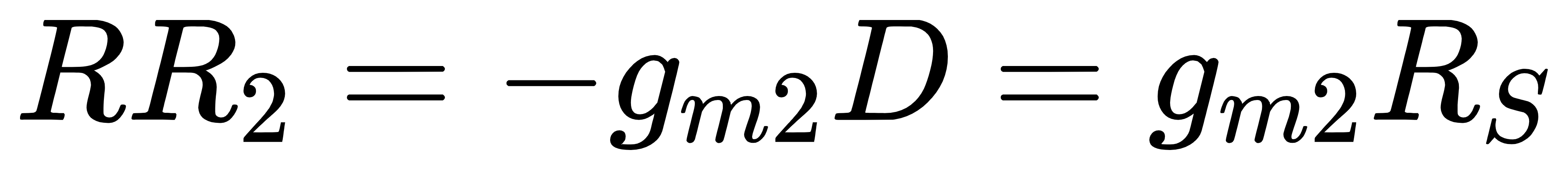
闭环电压增益

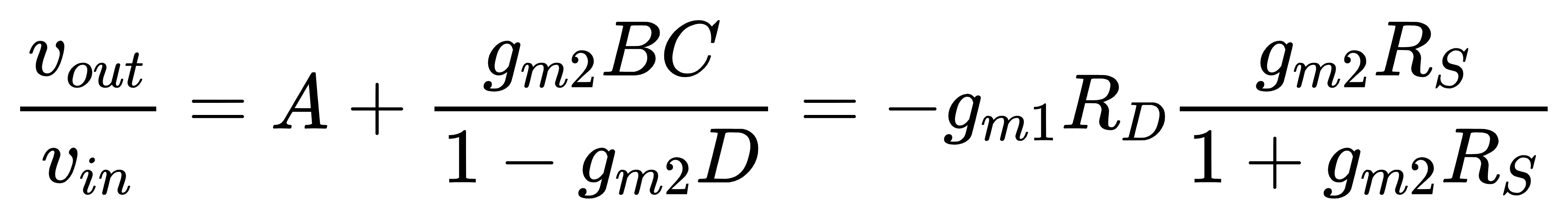
　　通过以上计算，并对比选择M1和选择M2计算的结果，可以得到如下结论：

（1）尽管选择不同晶体管计算得到的系数A~D可能不同，但是闭环增益的结果是相同的。

（2）不同晶体管的return ratio可能不同，这是由于不同的晶体管可能引入不同的反馈，或者一些晶体管不参与反馈（如本例子中的M1）。当晶体管处于反馈环路中时，则该晶体管的return ratio为该反馈环路的环路增益。如果某个晶体管的return ratio=0，则该晶体管不参与反馈。本例子中M2引入电流-电压反馈，将输出电流i_out反馈为电压v_f，与输入电压v_in作差后得到电压v_e，如图4所示。其中，前向放大倍数A_open=i_out/v_e=g_m2，反馈系数β=v_f/i_out=R_S，因此环路增益loop gain=A_openβ=g_m2R_S，与M2的return ratio相等。

图4 M2引入的电流-电压反馈

---

---

例2.利用Bode分析法计算图5所示电路的闭环增益（2种反馈机制，M1和M2处于不同反馈环路中）

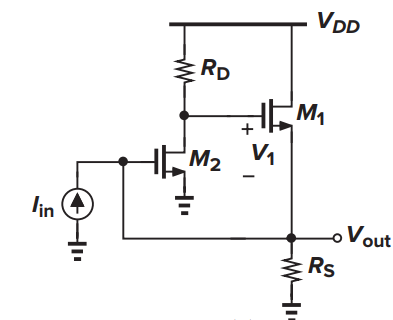
图5

　　该电路中，M1既参与局部的电流-电压反馈（与前一个例子中的source follower引入的反馈一样），又参与全局的电压-电流反馈，同时处在两个反馈环路中；而M2只参与全局的电压-电流反馈。

　　如果选择M1进行计算，当i₁=0时，流经电阻R_S的电流为i_in，可以得到A和C的值

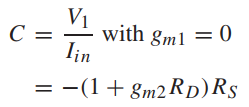
将i_in置零，可以得到B和D的值

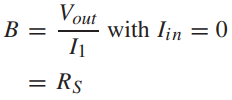
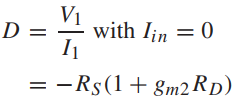
M1的return ratio为

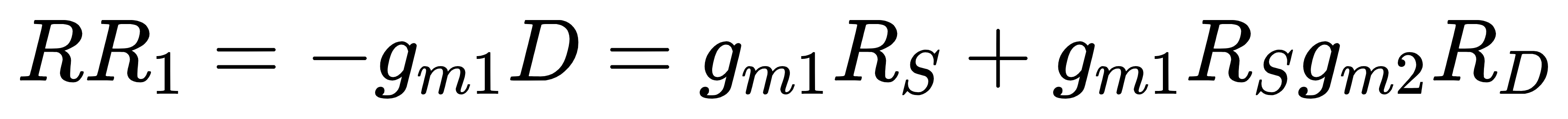
其中的g_m1R_S项与局部的电流-电压反馈有关，g_m1R_Sg_m2R_D项与全局的电压-电流反馈有关。闭环增益为

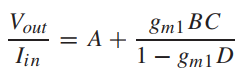
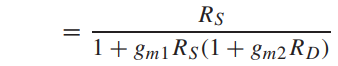
　　选择M2进行计算可以得到系数A~D的值为

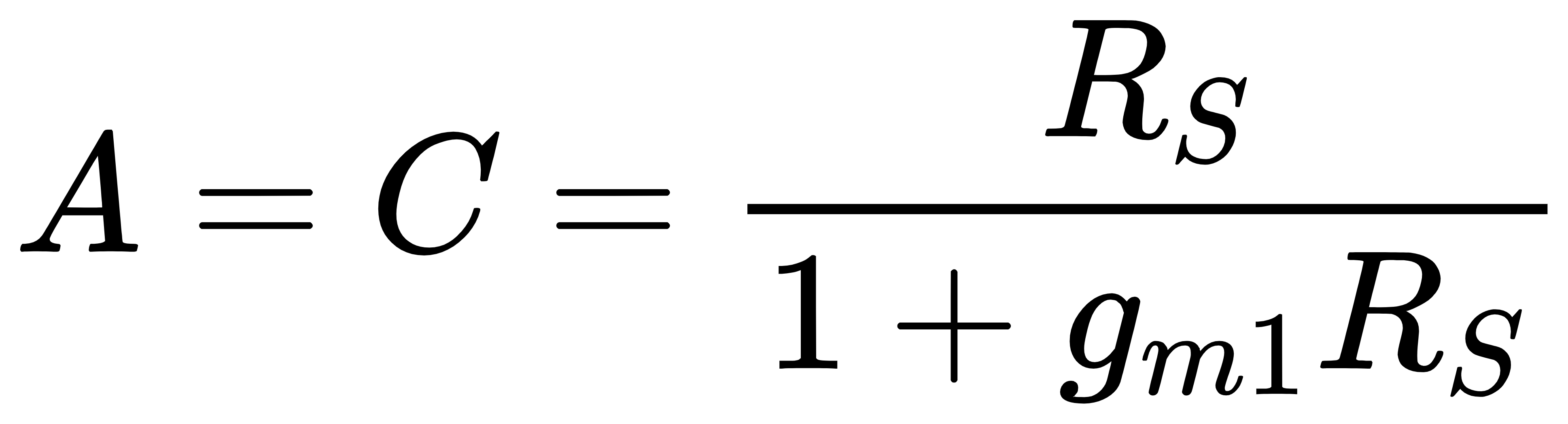
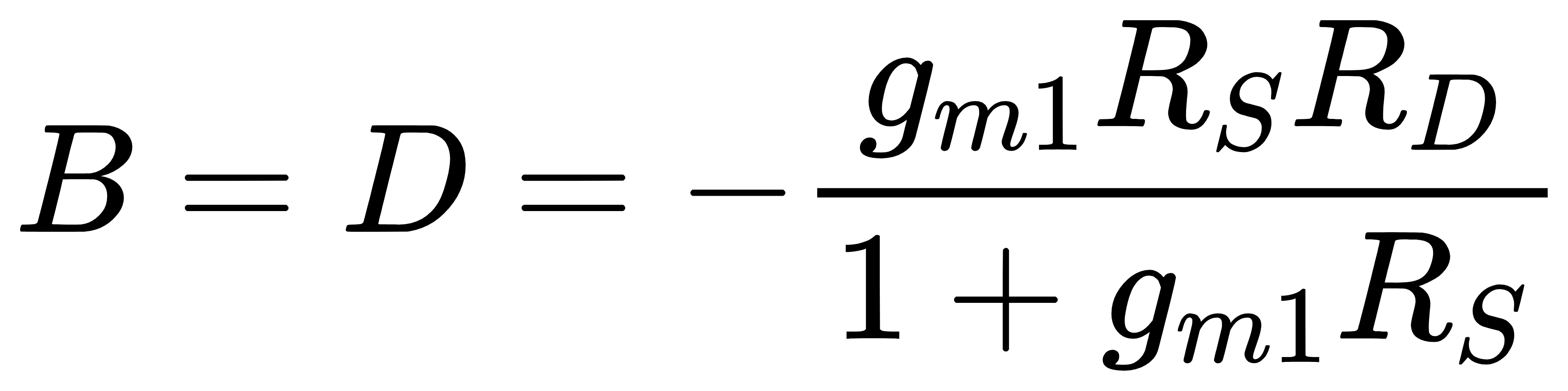
M2的return ratio为

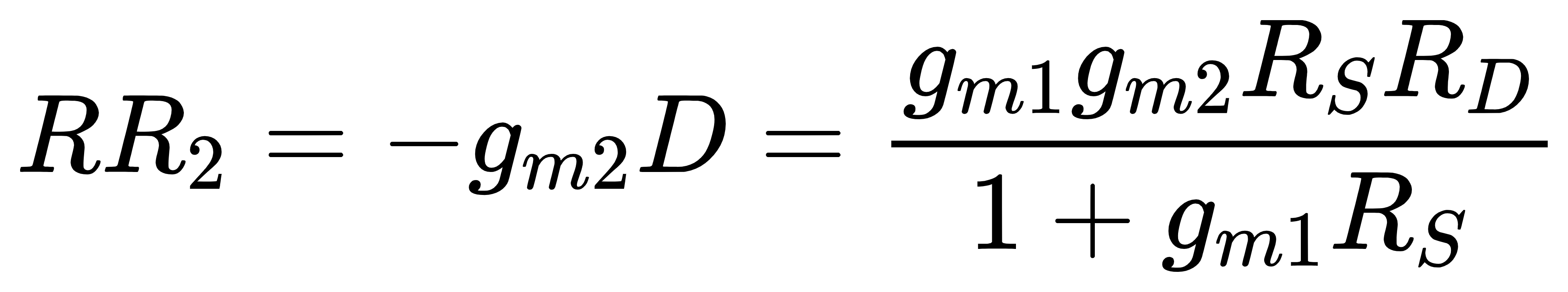
闭环增益为

---

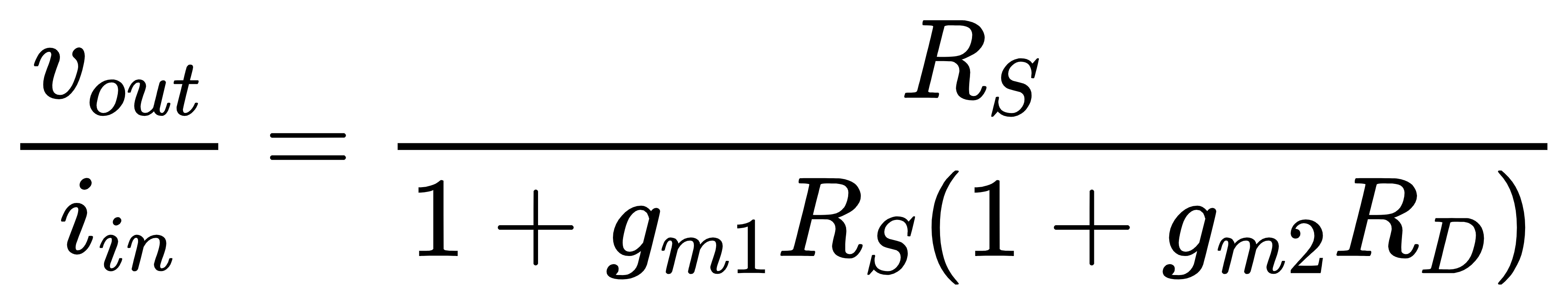
3 Blackman 阻抗定理

　　借助之前Bode 分析法的思想，如果我们将输出量定义为端口电压v_in，将输入量定义为同一端口的电流i_in，如图6所示，则有

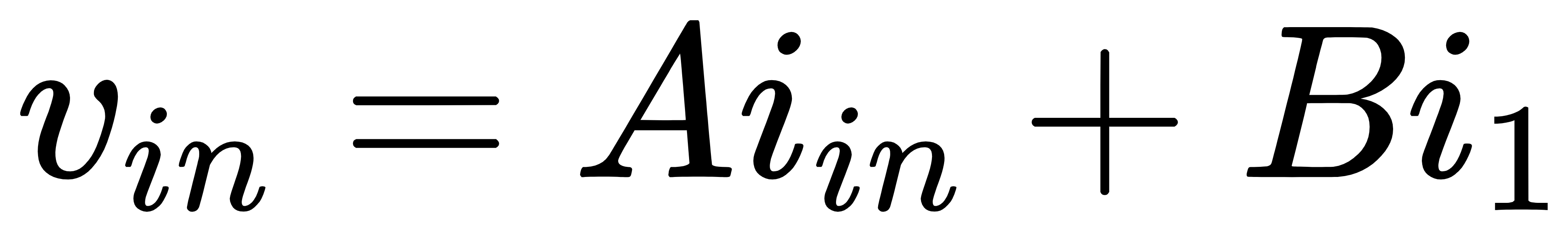
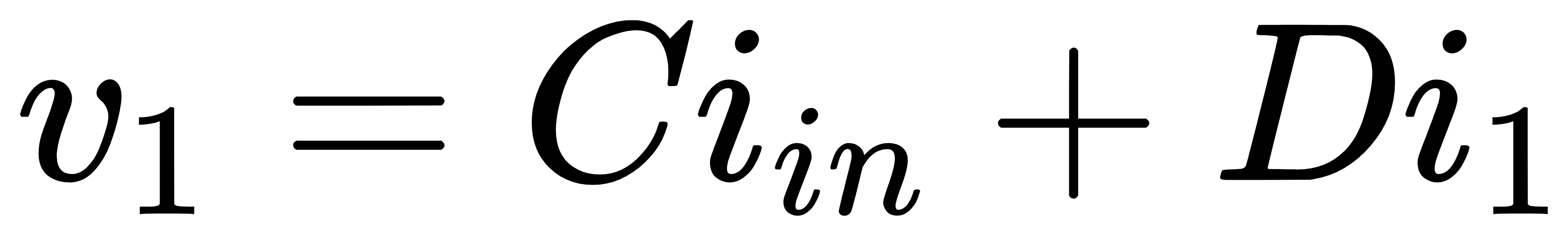
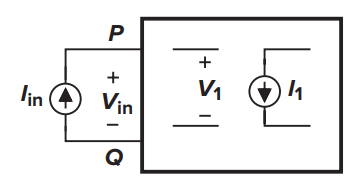
图6 Blackman 阻抗定理推导所用的电路模型

这个端口的阻抗Z_in=v_in/i_in，也可以看作是一种v_in对于i_in的“增益”，因此有

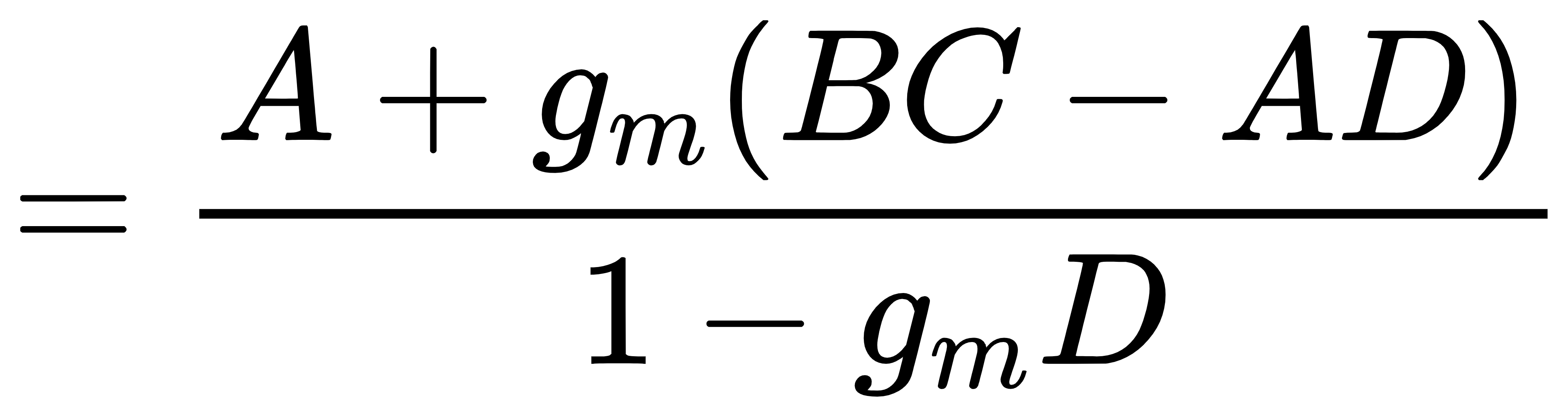
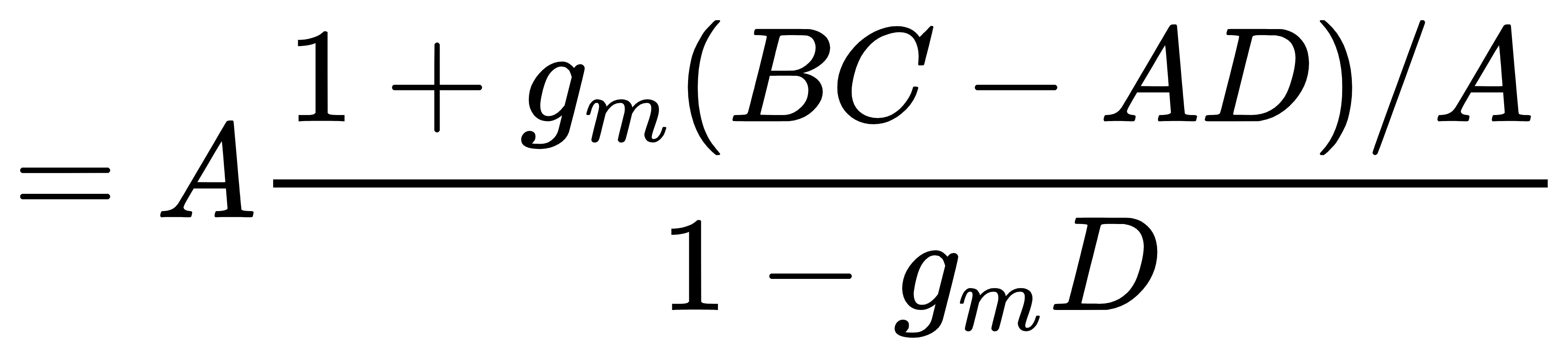
　　为了使上式变得更加直观，我们定义开路环路增益（open-circuit loop gain，T_OC）和短路环路增益（short-circuit loop gain，T_SC）两个量。开路环路增益的定义为：当i_in=0（端口开路）时，−g_mv₁/i₁的值（回忆在第2节中，return ratio=−g_mv₁/i₁可以理解为是环路增益），如图7所示。由于i_in=0，则有

由此可以得到开路环路增益

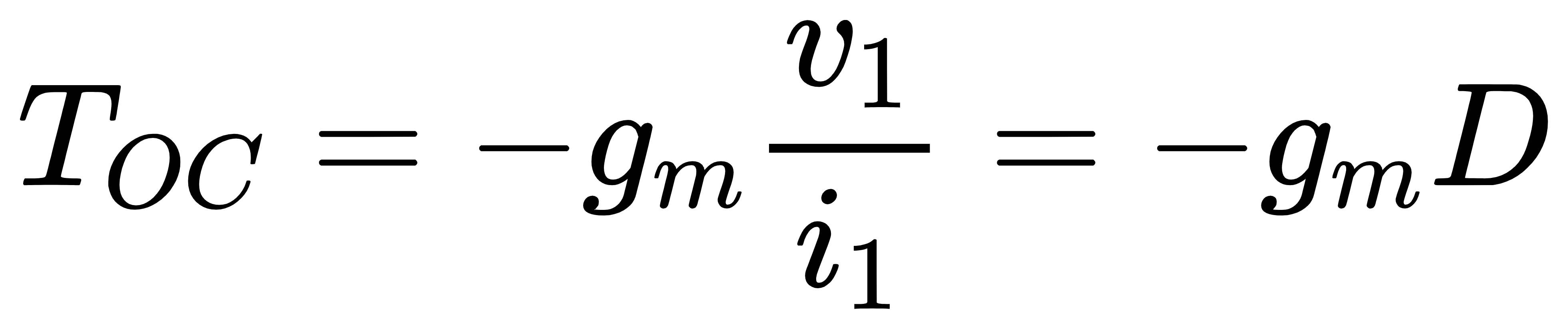
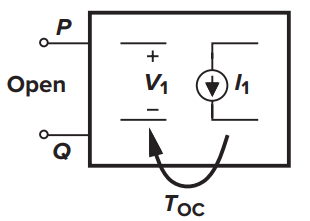
图7 开路环路增益的计算

类似地，短路环路增益的定义为：当v_in=0（端口短路）时，−g_mv₁/i₁的值，如图8所示。由于v_in=0，则有

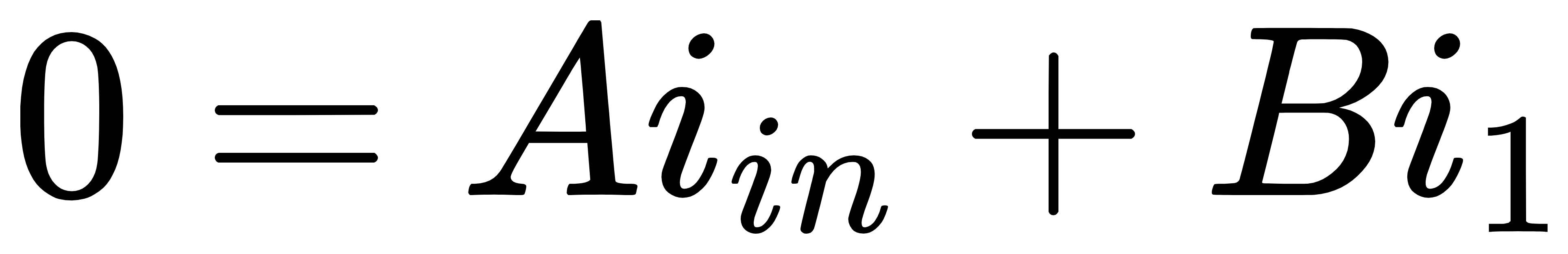
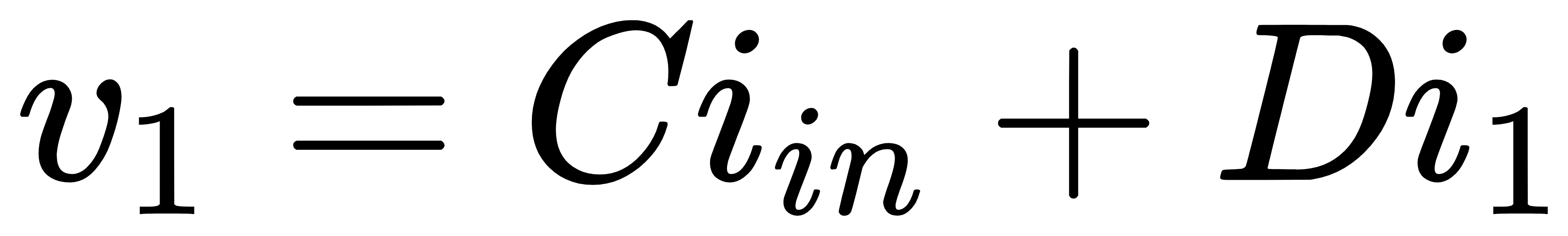
由此可以得到短路环路增益

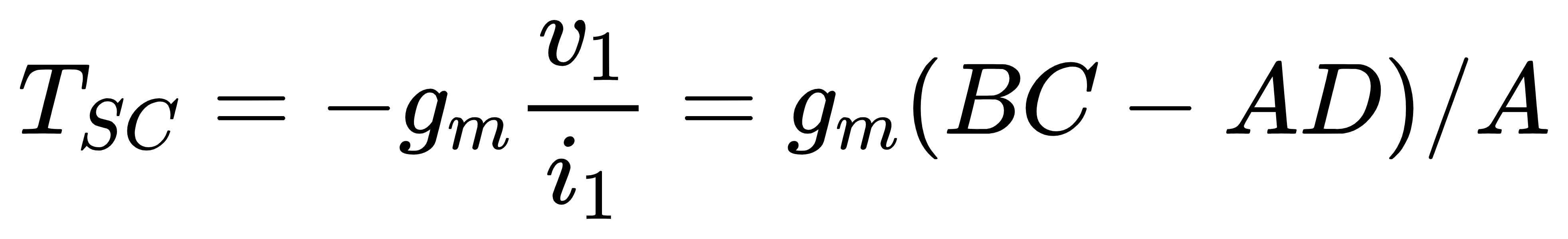
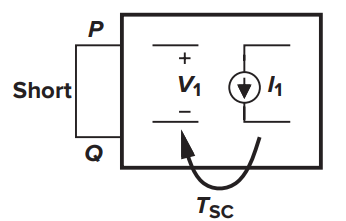
图8 短路环路增益的计算

　　结合Z_in、T_OC和T_SC的表达式，可以得到Blackman 阻抗定理：

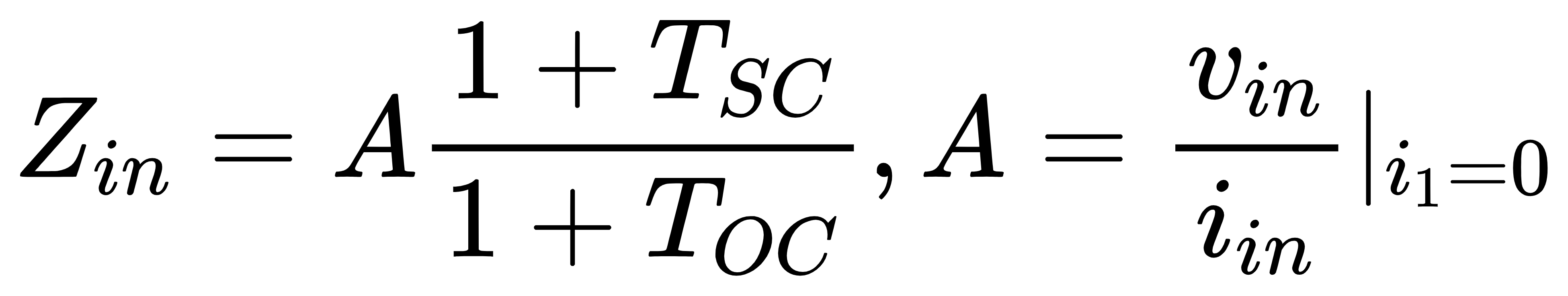
其中A是当晶体管被撤掉时的端口阻抗，即开环端口阻抗。因此要想计算端口阻抗，只需要计算A、T_OC和T_SC即可。另外，我们知道：

（1）当反馈类型为电压-电压反馈或者电流-电压反馈时，反馈网络向输入端反馈电压信号，其与输入端串联，输入阻抗Z_in=Z_in,open(1+T)，其中T为环路增益。

（2）当反馈类型为电压-电流反馈或者电流-电流反馈时，反馈网络向输入端反馈电流信号，其与输入端并联，输入阻抗Z_in=Z_in,open/(1+T)。

（3）当反馈类型为电压-电压反馈或者电压-电流反馈时，反馈网络检测输出端电压信号，其与输出端并联，输出阻抗Z_out=Z_out,open/(1+T)。

（4）当反馈类型为电流-电压反馈或者电流-电流反馈时，反馈网络检测输出端电流信号，其与输出端串联，输出阻抗Z_out=Z_out,open(1+T)。

将这四个阻抗表达式与Blackman 阻抗定理相比较，可知：

（1）在计算输入阻抗时，如果T_OC=0，则反馈网络只向输入端反馈电压信号，反馈网络与输入端纯串联；如果T_SC=0，则反馈网络只向输入端反馈电流信号，反馈网络与输入端纯并联。

（2）在计算输出阻抗时，如果T_SC=0，则反馈网络只检测输出电压信号，反馈网络与输入端纯并联；如果T_OC=0，则反馈网络只检测输出电流信号，反馈网络与输入端纯串联。

（3）如果T_OC和T_SC均不为0，则既有电压反馈，又有电流反馈。

4 渐进形式的闭环增益（Asymptotic Gain Form）

　　由第2节中推导得到的闭环增益表达式

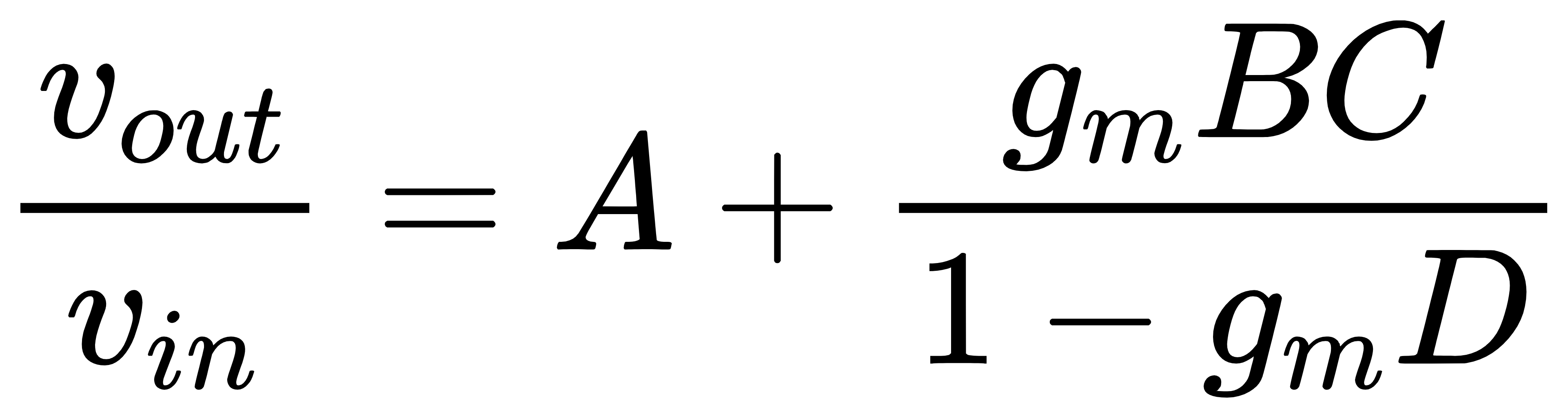
再进行延伸。当g_m=0时，v_out/v_in=A，因此将A记为H₀。下标0代表其为g_m=0时的闭环增益。当g_m→∞时，v_out/v_in=A–BC/D，因此将A–BC/D记为H_∞，下标∞代表其为g_m→∞时的闭环增益。又有return ratio的值T=–g_mD，因此闭环增益可以表示为

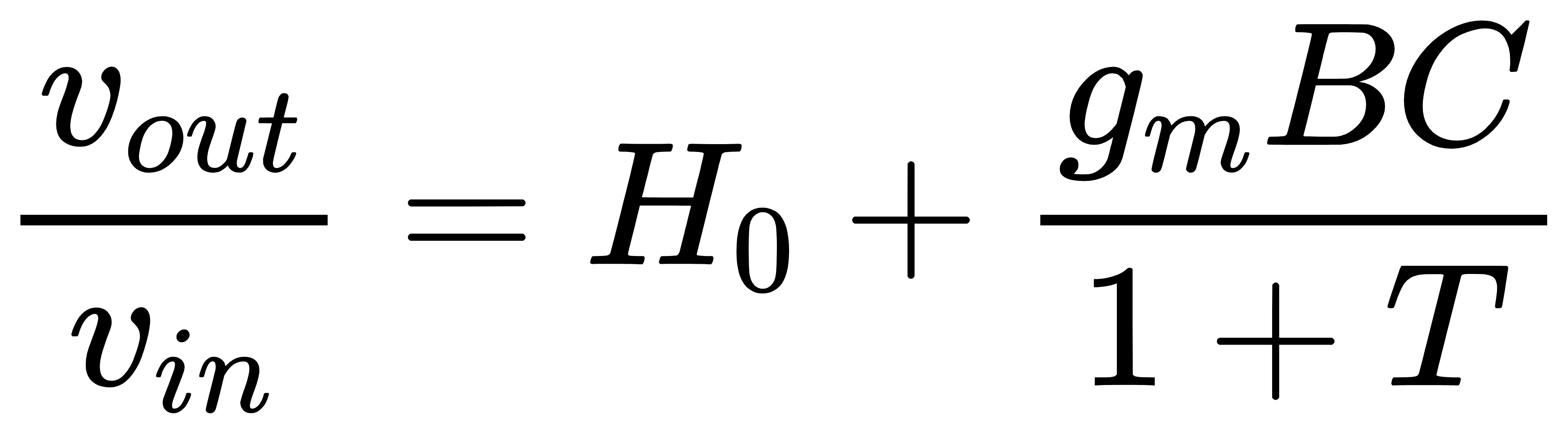
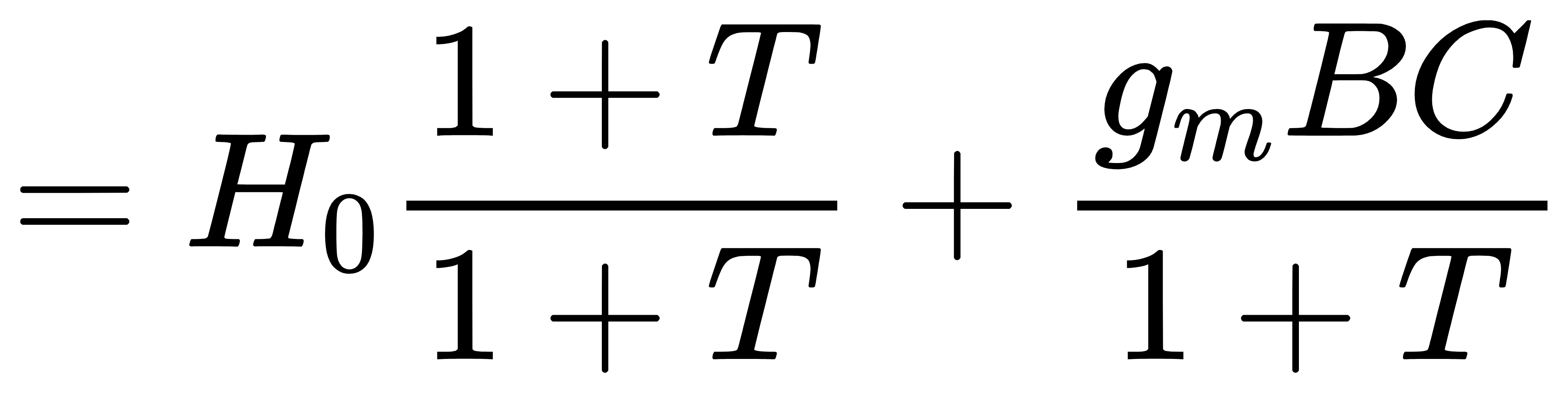
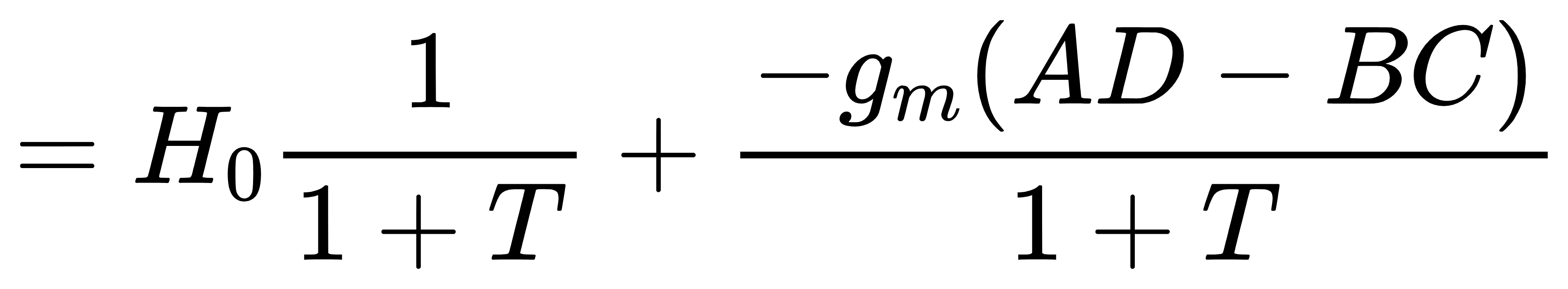
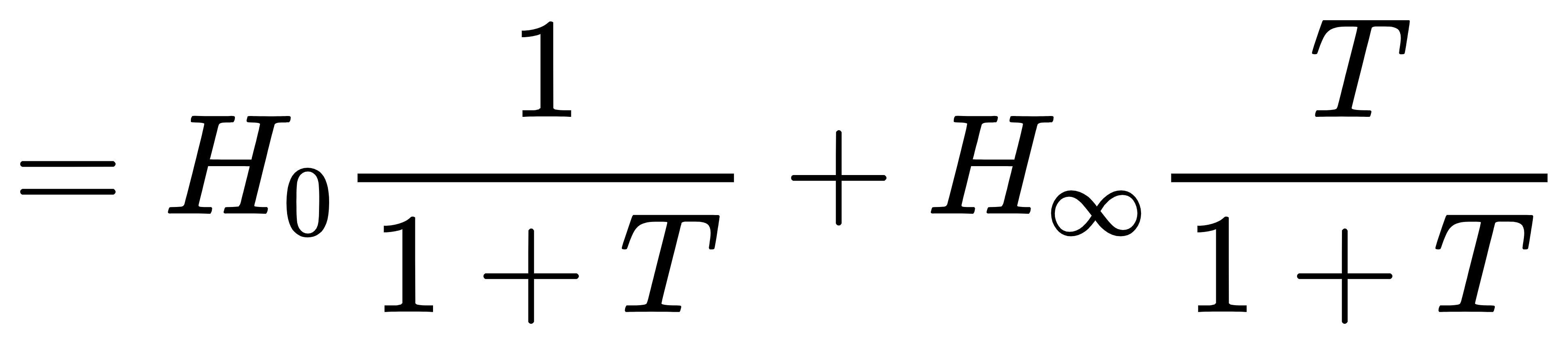
因此得到闭环增益的渐进形式：

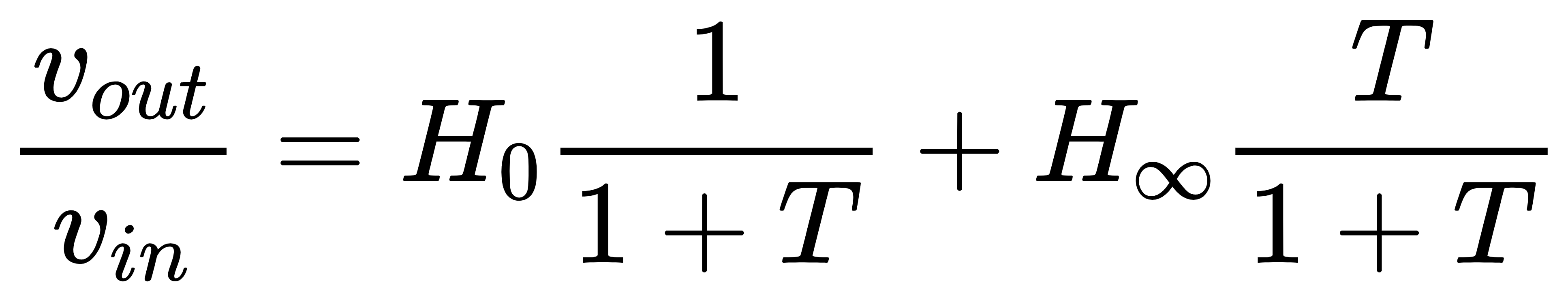
其中，H₀的意义为直接馈通增益，H_∞的意义为理想增益（即将放大器作虚短和虚断处理后，得到的增益1/β）。忽略反馈网络的直接馈通时（H₀=0），v_out/v_in=H_∞T/(1+T)，这与我们所熟知的公式v_out/v_in=A/(1+T)=(1/β)×T/(1+T)十分符合。