滑动窗口法——Leetcode例题

滑动窗口法——Leetcode例题（连更未完结）

1. 方法简介

滑动窗口法可以理解为一种特殊的双指针法，通常用来解决数组和字符串连续几个元素满足特殊性质问题（对于字符串来说就是子串）。滑动窗口法的显著特征是：两个指针同方向运动，且往往要对窗口内每个元素都加以处理。

滑动窗口法（以鄙人目前的程度）来看，大概可以分为两类：

1. 窗口的长度已知，此时双指针可以用一个指针和窗口长度常数来表示。
2. 窗口长度未知，往往对窗口内的元素都加以处理。

滑动窗口法实际上可以理解为是对暴力破解的优化，很多问题复杂度很高的暴力破解可以被简化为O(n)级别。根据目前我的经验来看，滑动窗口法的主要思路为如何减少窗口两端指针的重复变化，也就是两指针同向移动、不回溯，为了实现这个目标很多时候需要使用一些例如哈希表、哈希集合、队列等数据结构。

---

2. 解决字符串问题

2.1 LC——3 无重复最长子串

给定一个字符串 s ，请你找出其中不含有重复字符的 最长子串 的长度。

示例 1:
输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

示例 2:
输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

示例 3:
输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。
     请注意，你的答案必须是 子串 的长度，"pwke" 是一个子序列，不是子串。

提示：
0 <= s.length <= 5 * 104
s 由英文字母、数字、符号和空格组成

原题链接

2.1.1 问题分析

题目要求我们求出一个给定字符串的无重复最长子串。对于新手来说，最容易想到的应该是暴力算法，暴力算法是对每个字符开头的子串都加以遍历，直到出现重复元素为止，使用变量maxLength记录到目前为止最长的无重复子串长，遍历结束后输出maxLength即可。如果采用暴力算法时间复杂度(\(O(n^2)\))会很高，恐怕无法通过用例测试。

可以试着从暴力算法的缺点入手来优化它，暴力算法很麻烦的地方在于重复比较次数过多，以上面的示例一举例说明：

当指针start指向开头元素a时，end指针从0开始依次遍历，发现end = 3时，发生元素重复。那么就把start增加1，end指向start，重新开始，在这里b和c又比较了一次。可以预见，当每次start自增后，有大量的元素进行了重复比较。除此之外，每次检查是否有重复元素时也十分耗时（尤其是当被检查子串很长时）。

如何才能减少重复的比较呢？

首先我们来理解一下当出现重复元素时，如何移动指针才能减少无效比较次数。如下图所示，当f元素出现重复时，若采用暴力解法，start指针需要自增到b，然后end指针回溯，继续比较直到出现重复。可是我们可以发现，其实f重复了，以第一个f之前的元素作为start指针的位置都是不必要的，因为f总会再引起它们重复。所以，只需把start放到f的下一个位置就好，而且这样end指针无需回溯，极大地提高了效率。

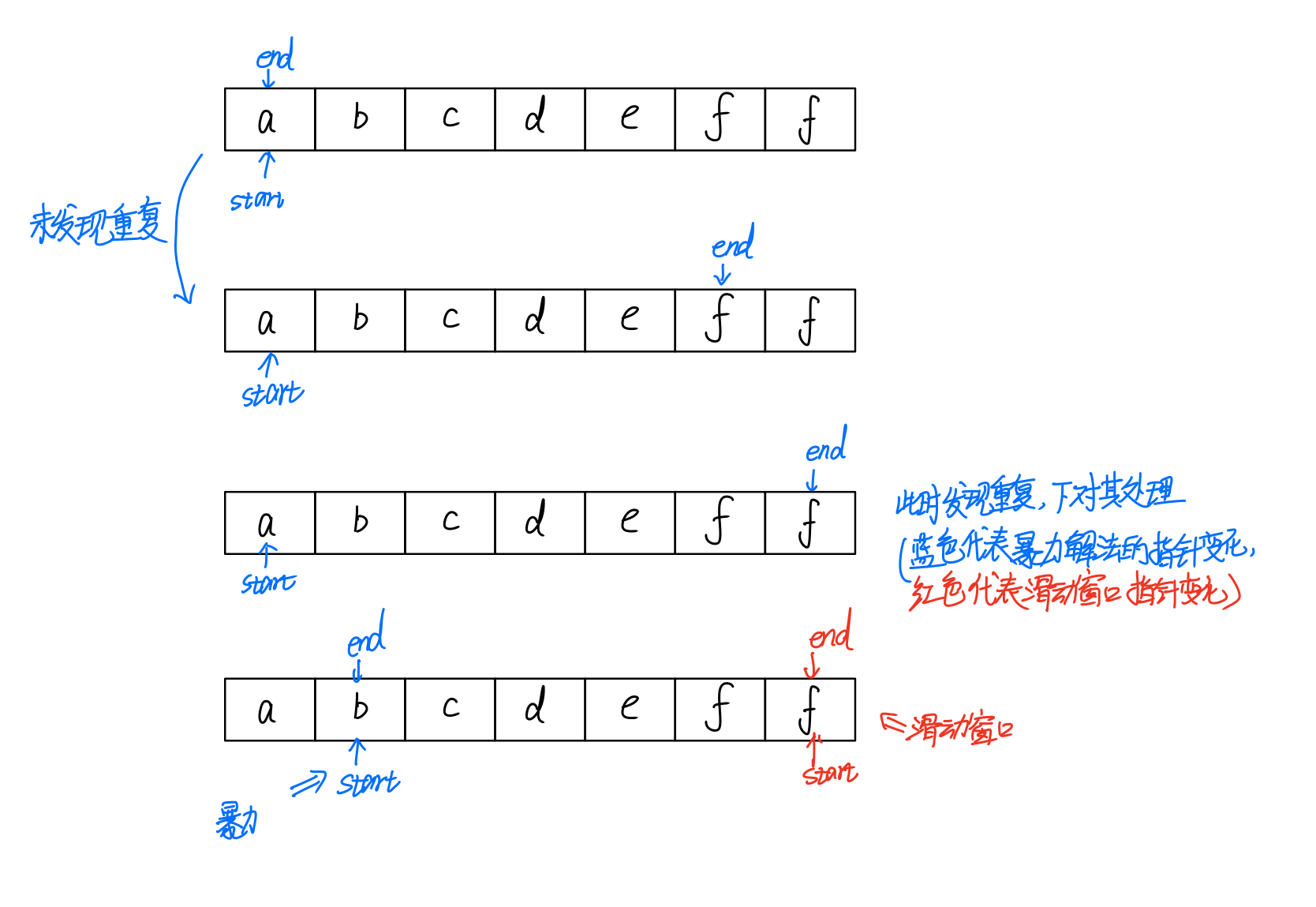
那么如何才能能实现这个操作呢？我们将哈希表存储的键值对更改为：<字符，字符发生重复时start指针应到达的位置>，事实上，我们通过上面的例子已经清楚了，start指针只需变化为当前子串内第一个重复字符的右侧即可。所以哈希表存储的键值对为<字符，位序>。

2.2.2 代码示例

class Solution {
    public int lengthOfLongestSubstring(String s) {
        Map<Character, Integer> map = new HashMap<>();
        int start = 0, end = 0;
        int ans = 0;
        while (end < s.length()) {
            if (map.containsKey(s.charAt(end)))
                start = Math.max(start, map.get(s.charAt(end))); // 要十分注意需要用max函数保证start指针不后退
            map.put(s.charAt(end), end + 1);
            ans = Math.max(ans, end - start + 1);
            end++;
        }
        return ans;
    }
}

代码分析

指针start和指针end同向移动且不回溯，时间复杂度为O(n)，相比于暴力解法是很大的提升。

2.2.3 总结

本题使用两个指针是比较显然的，但是如何利用HashMap解决暴力解法的指针频繁回溯问题是关键之处。这也是哈希表重要的应用体现。另外强烈推荐画手大鹏的动态示例，很有助于理解哦。

---

2.2 LC——219 存在重复元素Ⅱ

给你一个整数数组 nums 和一个整数 k ，判断数组中是否存在两个 不同的索引 i 和 j ，满足 nums[i] == nums[j] 且 abs(i - j) <= k 。如果存在，返回 true ；否则，返回 false 。

示例 1：
输入：nums = [1,2,3,1], k = 3
输出：true

示例 2：
输入：nums = [1,0,1,1], k = 1
输出：true

示例 3：
输入：nums = [1,2,3,1,2,3], k = 2
输出：false

提示：
1 <= nums.length <= 105
-109 <= nums[i] <= 109
0 <= k <= 105

原题链接

2.2.1 问题分析

这个问题显然可以使用滑动窗口法，而且窗口的长度即为k + 1。我们只需要设置一个集合（使用HashSet），用来记录遍历过的元素。在添加新元素之前，先判断集合内是否有相同的元素，如果有，则返回真。否则，就将其存入集合中。除此之外，还要判断添加新元素后集合的大小是否超出k （为什么不是k + 1呢？这是因为我们先判断是否有重复，若已有k个元素，且第k + 1个元素无重复，那么显然就不行，直接删除目前集合内最旧的元素），如果超出k则从集合中删除。

2.2.2 代码示例

暴力解法

class Solution {
    public boolean containsNearbyDuplicate(int[] nums, int k) {
        Map<Integer, Integer> map = new HashMap<>();
        if (k >= nums.length)
            k = nums.length - 1;
        for (int i = k; i < nums.length; i++) {
            for (int j = i - k; j <= i; j++) {
                if (map.containsKey(nums[j]))
                    return true;
                map.put(nums[j], j);
            }
            map = new HashMap<>();
        }
        return false;
    }
}
// 这种做法无法通过示例的时间复杂度测试

暴力解法甚至无法通过Leetcode的全部测试用例。

滑动窗口法

class Solution {
     public boolean containsNearbyDuplicate(int[] nums, int k) {
         Set<Integer> set = new HashSet<>();
         for (int i = 0; i < nums.length; i++) {
             if (set.contains(nums[i]))
                 return true;
            set.add(nums[i]);
            if (set.size() > k)
                set.remove(nums[i - k]);
         }
         return false;
    }
}

---

2.3 LC——643 子数组最大平均数Ⅰ

给你一个由 n 个元素组成的整数数组 nums 和一个整数 k 。

请你找出平均数最大且 长度为 k 的连续子数组，并输出该最大平均数。

任何误差小于 \(10^{-5}\)的答案都将被视为正确答案。

示例 1：
输入：nums = [1,12,-5,-6,50,3], k = 4
输出：12.75
解释：最大平均数 (12-5-6+50)/4 = 51/4 = 12.75

示例 2：
输入：nums = [5], k = 1
输出：5.00000

提示：
n == nums.length
1 <= k <= n <= 105
-104 <= nums[i] <= 104

原题链接

2.3.1 问题分析

这道题跟219题看起来十分相似，其也可以滑动窗口法。连续子数组长度固定，要求平均数最大的连续子数组也就是求元素和最大的连续子数组。最简单的思路是暴力解法，选定一个指针i，其取值范围为[k - 1，n - 1]，在选定i的情况下选定指针j，其取值范围为[i - k, i]，利用j对子数组元素求和，求出所有子数组的元素和后即可得到最大者。

暴力解法的时间复杂度为\(O(n^2)\)，而且像上一道例题一样，做了大量的、重复的计算。当i为k - 1时（第一次计算），可以求出前k个元素组成连续子数组的元素和，当i为k时（第二次计算），我们得到第2个元素到第k个元素组成的连续子数组元素和，但是中间k - 2个元素的和我们计算了两次。该如何解决呢？

可以采用滑动窗口的思想解决，也就是我们先计算前k个元素和，然后利用其值计算第二个数组元素和，见下面推导：

\[\begin{align}
sum_1 &= a_0 + a_1+...+a_{k-1} \\
sum_2 &= a_1 + a_2 + ... + a_{k-1} + a_{k} \\
&= sum_1 - a_0 + a_{k}\\
sum_i &= sum_{i-1} - a_{i-k} + a_i
\end{align}
\]

利用该公式，计算新的元素和只需在上一个元素和上微调一下即可。

2.3.2 代码示例

暴力解法

class Solution {
    public double findMaxAverage(int[] nums, int k) {
        int maxSum = 0;
        int nowSum = 0;
        for (int i = 0; i < nums.length - k + 1; i++) {
            for (int j = i; j < k + i; j++)
                nowSum += nums[j];
            if (i == 0)
                maxSum = nowSum;
            maxSum = Math.max(maxSum, nowSum);
            nowSum = 0;
        }
        return (double)maxSum / k;
    }
}

滑动窗口法

class Solution {
    public double findMaxAverage(int[] nums, int k) {
        int maxSum;
        int subSum = 0;
        for (int i = 0; i < k; i++) {
            subSum += nums[i];
        }
        maxSum = subSum;
        for (int i = k; i < nums.length; i++) {
            subSum = subSum + nums[i] - nums[i - k];
            maxSum = Math.max(subSum, maxSum);
        }
        return (double)maxSum / k;
    }
}