P3272 [SCOI2011]地板

\(\color{#0066ff}{ 题目描述 }\)

lxhgww的小名叫”小L“，这是因为他总是很喜欢L型的东西。小L家的客厅是一个R*C的矩形，现在他想用L型的地板来铺满整个客厅，客厅里有些位置有柱子，不能铺地板。现在小L想知道，用L型的地板铺满整个客厅有多少种不同的方案？需要注意的是，如下图所示，L型地板的两端长度可以任意变化，但不能长度为0。

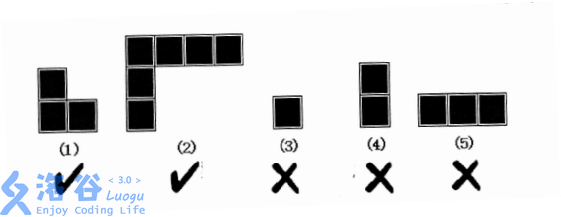
铺设完成后，客厅里面所有没有柱子的地方都必须铺上地板，但同一个地方不能被铺多次。

\(\color{#0066ff}{输入格式}\)

输入的第一行包含两个整数，R和C，表示客厅的大小。接着是R行，每行C个字符。'_'表示对应的位置是空的，必须铺地板；'*'表示对应的位置有柱子，不能铺地板。

\(\color{#0066ff}{输出格式}\)

输出包含q行，第i行为m[i]个整数，该行的第j(j=1，2...，，m[i])个数表示第i年被授权的聚居地h[j]的临时议事处管理的种族个数。

\(\color{#0066ff}{输入样例}\)

3 3
___
_*_
___

\(\color{#0066ff}{输出样例}\)

8

\(\color{#0066ff}{数据范围与提示}\)

测试点编号      数据范围
1,2             R*C<=25
3-5             R*C<=100并且（R=2或者C=2）
6-10            R*C<=100

\(\color{#0066ff}{ 题解 }\)

一道不错的插头DP

情况要考虑全面

考虑插头，0：无，1：未拐弯插头，2：已拐弯插头（题中要求必须是拐弯的砖）

套板子就行啦

再次声明，我TM就不写hash表，暴力卡常开\(O2\)，980ms卡过去！！！

// luogu-judger-enable-o2
#include<bits/stdc++.h>
#define LL long long
LL in() {
	char ch; LL x = 0, f = 1;
	while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
	for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
	return x * f;
}
std::unordered_map<int, int> f[2];
int n, m, s, t;
bool mp[120][120];
char getch() {
	char ch = getchar();
	while(ch != '*' && ch != '_') ch = getchar();
	return ch;
}
void init() {
	n = in(), m = in();
	static bool cp[120][120];
	for(int i = 1; i <= n; i++)
		for(int j = 1; j <= m; j++)
			cp[i][j] = getch() == '_';
	if(m > n) {
		std::swap(n, m);
		for(int i = 1; i <= n; i++)
			for(int j = 1; j <= m; j++) {
				mp[i][j] = cp[j][i];
				if(mp[i][j]) s = i, t = j;
			}
	}
	else {
		for(int i = 1; i <= n; i++)
			for(int j = 1; j <= m; j++) {
				mp[i][j] = cp[i][j];
				if(mp[i][j]) s = i, t = j;
			}
	}
}
const int mod = 20110520;
int pos(int v, int x) { return (v << (x << 1LL)); }
void ins(int &x, int y) { x %= mod, (x += y) %= mod; }
int work() {
	int now = 0, nxt = 1;
	int ans = 0;
	f[now][0] = 1;
	int U = (1 << ((m + 1) << 1)) - 1;
	for(int i = 1; i <= n; i++) {
		for(int j = 1; j <= m; j++) {
			f[nxt].clear();
			for(auto &k:f[now]) {
				int S = k.first, val = k.second;
				int L = (S >> ((j - 1) << 1)) & 3, R = (S >> (j << 1)) & 3;
				if(!mp[i][j]) {
					if(!L && !R) ins(f[nxt][S], val);
					continue;
				}
				if(!L && !R) {
					//right 1
					if(mp[i][j + 1]) ins(f[nxt][S ^ pos(1, j)], val);
					//down 1
					if(mp[i + 1][j]) ins(f[nxt][S ^ pos(1, j - 1)], val);
					//middle double 2
					if(mp[i][j + 1] && mp[i + 1][j]) ins(f[nxt][S ^ pos(2, j - 1) ^ pos(2, j)], val);
				}
				//要么直走还是1，要么拐弯变成2
				else if(L == 0 && R == 1) {
					if(mp[i + 1][j]) ins(f[nxt][S ^ pos(1, j - 1) ^ pos(1, j)], val);
					if(mp[i][j + 1]) ins(f[nxt][S ^ pos(1, j) ^ pos(2, j)], val);
				}
				//要么直走还是2，要么停下变成0
				else if(L == 0 && R == 2) {
					if(mp[i + 1][j]) ins(f[nxt][S ^ pos(2, j - 1) ^ pos(2, j)], val);
					ins(f[nxt][S ^ pos(2, j)], val);
				}
                 //跟上面差不多
				else if(L == 1 && R == 0) {
					if(mp[i][j + 1]) ins(f[nxt][S ^ pos(1, j - 1) ^ pos(1, j)], val);
					if(mp[i + 1][j]) ins(f[nxt][S ^ pos(1, j - 1) ^ pos(2, j - 1)], val);
				}
				else if(L == 2 && R == 0) {
					if(mp[i][j + 1]) ins(f[nxt][S ^ pos(2, j - 1) ^ pos(2, j)], val);
					ins(f[nxt][S ^ pos(2, j - 1)], val);
				}
                 //必须拼上，没有其他情况
				else if(L == 1 && R == 1) {
					ins(f[nxt][S ^ pos(1, j - 1) ^ pos(1, j)], val);
				}
                 //这些情况都是不成立的
				else if(L == 1 && R == 2) {}
				else if(L == 2 && R == 1) {}
				else if(L == 2 && R == 2) {}
				if(i == s && j == t) {
                      //1 1 // 0 2 // 2 0 第一个是接上，后两个是直接停下，都可以收集ans
					if(L + R == 2) ins(ans, val);
				}
			}
			std::swap(now, nxt);
		}
		f[nxt].clear();
		for(auto &k:f[now]) ins(f[nxt][(k.first << 2) & U], k.second);
		std::swap(nxt, now);
	}
	return ans;
}
int main() {
	init();
	printf("%d\n", work() % mod);
	return 0;
}