吴恩达机器学习笔记（二） —— Logistic回归

主要内容：

一.回归与分类

二.Logistic模型即sigmoid function

三.decision boundary 决策边界

四.cost function 代价函数

五.梯度下降

六.自带求解函数

七.多分类问题

一.回归与分类

回归：用于预测，输出值是连续型的。例如根据房子的大小预测房子的价格，其价格就是一个连续型的数。

分类：用于判别类型，输出值是离散型的（或者可以理解为枚举型，其所有的输出值是有限的且已知的），例如根据肿瘤的大小判断其是恶行肿瘤还是良性肿瘤，其输出值就是0或1。

二.Logistic模型即sigmoid function

1.logistic模型可很好地应用于分类问题上，它可以解决二分类以及多分类问题。其基础是利用sigmoid function进行二分类。

sigmoid function：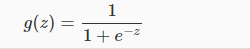

其图像如下：

可以看得出，g(z)的至于为(0,1)，且当z<-2.5时，g(z)非常接近0；当z>2.5时，g(z)非常接近1。因此该函数非常适用于做二分类。

2.为了将其应用到二分类问题上，需要对其做一下变形：

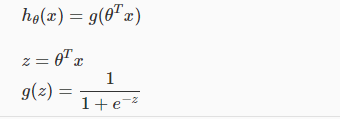
即：

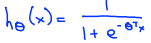(从讲义中直接截图的，把hΘ(x)改成hΘ(z)就对了)

其中，hΘ(z)的值就是y=1（y表示输出值是哪一类）的概率，1-hΘ(z)就是y=0的概率。

当hΘ(z)>=0.5时，可断定y=1；当hΘ(z)<0.5时，可断定y=0。

三.decision boundary 决策边界

1.我们知道了当hΘ(z)>=0.5时，y=1；当hΘ(z)<0.5时，y=0。那怎么判断hΘ(z)的值是大于还是小于0.5呢？

可知，当hΘ(z)>=0.5时，z>=0； hΘ(z)<0.5时， z<0。

由于z = Θ'x，所以：当hΘ(z)>=0.5时，Θ'x>=0； hΘ(z)<0.5时， Θ'x<0。

所以我们最主要的工作就是判断Θ'x是大于0还是小于0，而由于Θ'x的值决定着不同的类别，因此，函数 f(x) = Θ'x 也就成为了划分两个不同类别的分界线（或者叫超平面，因为可以是多维的）。

2.看以下例子：

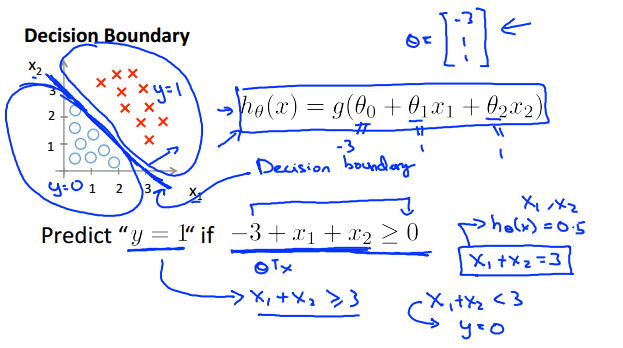
这里的z即f(x) = x1+x2-3，当f(x)>=0时，即 位于直线上面的那一部分属于类别1，位于直线下面的那一部分为类别0。

此例子的决策边际是线性的，但还可以是非线性的，如下：

决策边界为 f(x) = x1^2 + x2^2 - 1，即一个单位圆。当f(x)>=0时，即在圆以外的部分属于类别1；当f(x)<0，在圆以内的部分为类别0。

上面介绍的两个例子都是只有两个属性，即x1和x2，当属性为三个或者更多时，决策边界就为一个平面或者是超平面，总之能把空间一分为二就行了。

3.综上：z = 0即为决策边界，位于z>0一边的为类别1，位于z<0一边的为类别0。

四.cost function 代价函数

明白了决策边界是怎么工作，之后就是最重要的就是找出决策边界，也就是通过学习，得出参数Θ（其中特征x需要预先对数据进行判断，然后再选择合适的类型，就如上面圆的那个例子，或者说把所有参数的组合都列出来）。

整理一下接下来的工作：

1.选择的模型为：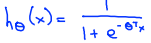

2.通过数据集，训练出Θ。

所以，就要确定一下这个模型的代价函数了：

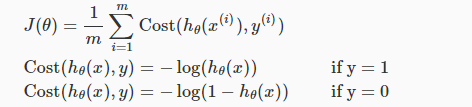
其图像为：

            

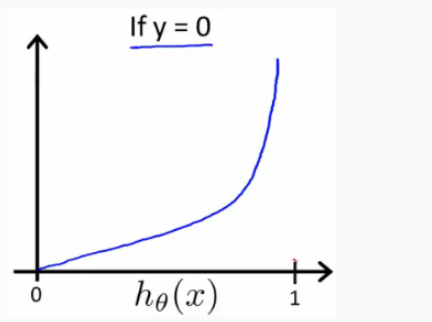
可知，当hΘ(x)-->0，但实际值y=1时，代价接近无穷大；当hΘ(x)-->1时，实际值y=1时，代价接近0。即判断错误的代价很高，而判断正确的代价几乎为0，所以作为代价函数是很合适的。

其中，我们可以把y=0和y=1的两种情况合并到一条公式当中：

所以，整体的代价函数为：

将其向量化：

五.梯度下降

有了代价函数J(Θ)之后，就可以用梯度下降来求出Θ了。

迭代的伪代码：

，即：

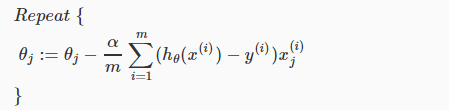
向量化后：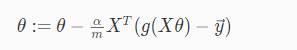

这里有个高数的问题，对J(Θ)求导貌似不太直观，那就动手试一试：

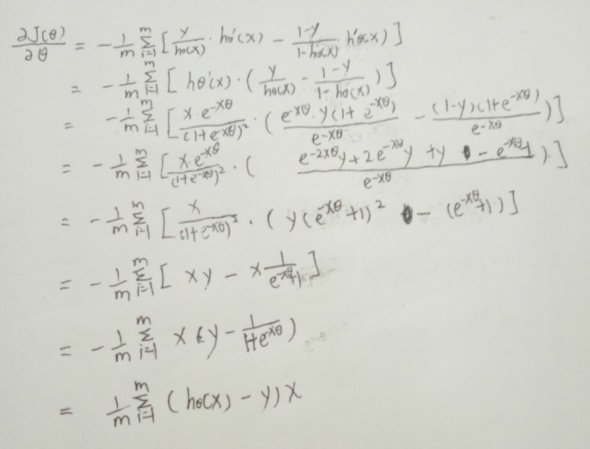
六.自带求解函数

用法如下：

需要自己实现costFunction函数，其中(t)的意思是：costFunction中参数t是initial_theta，即把initial_theta带入到t中。

其返回值为求出的解，即最优解theta和在此条件下的损失值。

（这个函数没用过，不太清楚，日后再尝试一下）

七.多分类问题

当类别多于两个时，仍然可以使用logistic回归对其进行分类，这种方法就是：One-vs-all，俗称“一对多”。

思路：枚举每一种类别，找出其与剩下类别的决策边界，即通过数据集，训练出每一类别与其他类别的hΘ(x)函数。假如用n+1个类别，就用n+1个hΘ(x)函数。当输入一个x时，就将其带入带每一个hΘ(x)函数中，取最大值的那个函数，就是x所对应的分类。

如下：

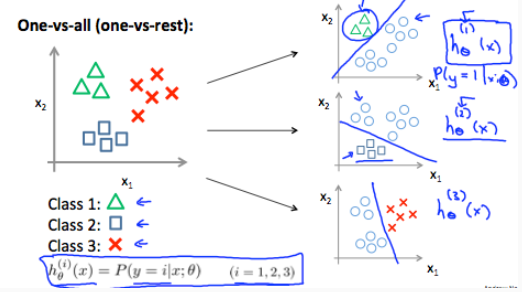（训练出n+1个hΘ(x)函数）

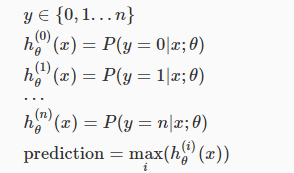（概率最大的那个，便是它所在的分类）