jzoj5986. 【WC2019模拟2019.1.4】立体几何题 （权值线段树）

传送门

题面

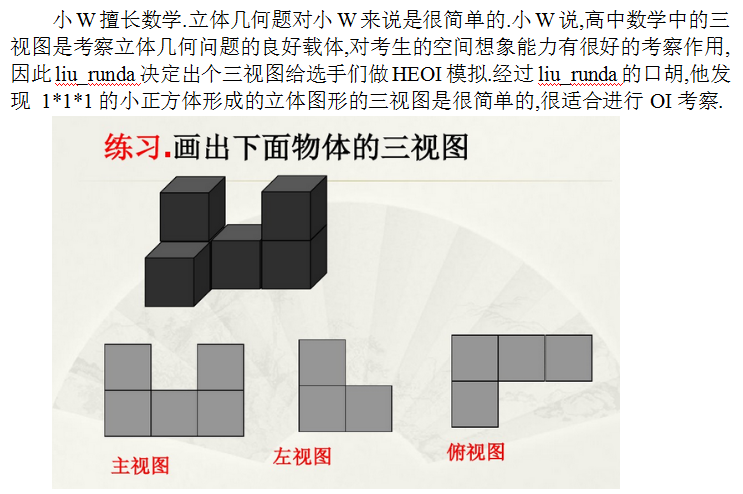
题解

不难看出每个点的大小为行列限制中较小的那一个（因为数据保证有解）

对于行的每个限制，能取到的个数是列里限制大于等于它的数的个数，同理，对于列是行里大于它的个数（这里没有等于，为了避免重复计算）

于是可以对于行列分别开权值线段树，修改的时候只要把对应的贡献改一下就好了

//minamoto
#include<bits/stdc++.h>
#define R register
#define ll long long
#define fp(i,a,b) for(R int i=a,I=b+1;i<I;++i)
#define fd(i,a,b) for(R int i=a,I=b-1;i>I;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;}
using namespace std;
char buf[1<<21],*p1=buf,*p2=buf;
inline char getc(){return p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++;}
int read(){
    R int res,f=1;R char ch;
    while((ch=getc())>'9'||ch<'0')(ch=='-')&&(f=-1);
    for(res=ch-'0';(ch=getc())>='0'&&ch<='9';res=res*10+ch-'0');
    return res*f;
}
char sr[1<<21],z[20];int C=-1,Z=0;
inline void Ot(){fwrite(sr,1,C+1,stdout),C=-1;}
void print(R ll x){
    if(C>1<<20)Ot();if(x<0)sr[++C]='-',x=-x;
    while(z[++Z]=x%10+48,x/=10);
    while(sr[++C]=z[Z],--Z);sr[++C]='\n';
}
const int N=1e5+5;
struct change{int op,pos,x;}c[N];
ll res;int n,m,a[N],b[N],aa[N],bb[N],op,pos,x,lim;
struct seg{
	struct node{int ls,rs,cnt;ll sum;}t[N<<5];
	int rt,tot;
	void ins(int &p,int l,int r,int x,int ty){
		if(!p)p=++tot;t[p].cnt+=ty,t[p].sum+=x*ty;
		if(l==r)return;int mid=(l+r)>>1;
		x<=mid?ins(t[p].ls,l,mid,x,ty):ins(t[p].rs,mid+1,r,x,ty);
	}
	int q_cnt(int p,int l,int r,int ql,int qr){
		if(!p)return 0;if(ql<=l&&qr>=r)return t[p].cnt;
		int mid=(l+r)>>1,res=0;
		if(ql<=mid)res+=q_cnt(t[p].ls,l,mid,ql,qr);
		if(qr>mid)res+=q_cnt(t[p].rs,mid+1,r,ql,qr);
		return res;
	}
	ll q_sum(int p,int l,int r,int ql,int qr){
		if(!p)return 0;if(ql<=l&&qr>=r)return t[p].sum;
		int mid=(l+r)>>1;ll res=0;
		if(ql<=mid)res+=q_sum(t[p].ls,l,mid,ql,qr);
		if(qr>mid)res+=q_sum(t[p].rs,mid+1,r,ql,qr);
		return res;
	}
}A,B;
int main(){
	freopen("graph.in","r",stdin);
	freopen("graph.out","w",stdout);
	n=read();
	fp(i,1,n)aa[i]=a[i]=read(),cmax(lim,a[i]);
	fp(i,1,n)bb[i]=b[i]=read(),cmax(lim,b[i]);
	m=read();
	fp(i,1,m)c[i].op=read(),c[i].pos=read(),c[i].x=read(),cmax(lim,c[i].x);
	sort(aa+1,aa+1+n),sort(bb+1,bb+1+n);
	for(R int i=1,j=1;i<=n;++i){
		while(j<=n&&aa[i]>bb[j])++j;
		res+=1ll*aa[i]*(n-j+1);
	}for(R int i=1,j=1;i<=n;++i){
		while(j<=n&&bb[i]>=aa[j])++j;
		res+=1ll*bb[i]*(n-j+1);
	}print(res);
	fp(i,1,n)A.ins(A.rt,0,lim,a[i],1);
	fp(i,1,n)B.ins(B.rt,0,lim,b[i],1);
	fp(i,1,m){
		op=c[i].op,pos=c[i].pos,x=c[i].x;
		if(op==0){
			res-=1ll*B.q_cnt(B.rt,0,lim,a[pos],lim)*a[pos];
			if(a[pos]>0)res-=B.q_sum(B.rt,0,lim,0,a[pos]-1);
			A.ins(A.rt,0,lim,a[pos],-1);
			a[pos]=x;
			A.ins(A.rt,0,lim,a[pos],1);
			res+=1ll*B.q_cnt(B.rt,0,lim,a[pos],lim)*a[pos];
			if(a[pos]>0)res+=B.q_sum(B.rt,0,lim,0,a[pos]-1);
		}else{
			if(b[pos]<lim)res-=1ll*A.q_cnt(A.rt,0,lim,b[pos]+1,lim)*b[pos];
			res-=A.q_sum(A.rt,0,lim,0,b[pos]);
			B.ins(B.rt,0,lim,b[pos],-1);
			b[pos]=x;
			B.ins(B.rt,0,lim,b[pos],1);
			if(b[pos]<lim)res+=1ll*A.q_cnt(A.rt,0,lim,b[pos]+1,lim)*b[pos];
			res+=A.q_sum(A.rt,0,lim,0,b[pos]);
		}print(res);
	}return Ot(),0;
}