对卷积(convolution)的理解
np.convolve([1,2,3,4],[1,1,3],'full') 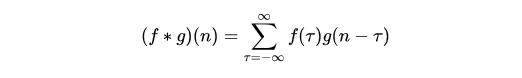
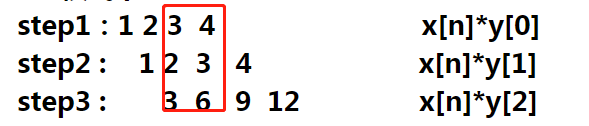
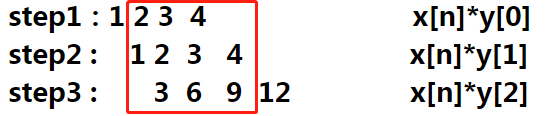
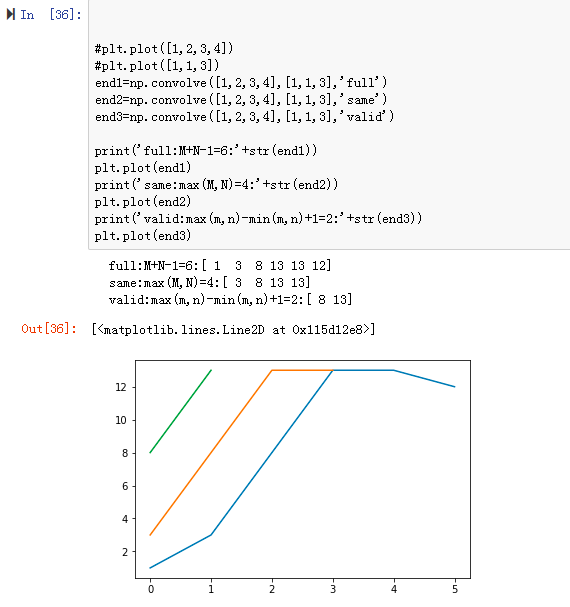
对卷积(convolution)的理解的更多相关文章
- 最容易理解的对卷积(convolution)的解释
啰嗦开场白 读本科期间,信号与系统里面经常讲到卷积(convolution),自动控制原理里面也会经常有提到卷积.硕士期间又学了线性系统理论与数字信号处理,里面也是各种大把大把卷积的概念.至于最近大火 ...
- 卷积神经网络CNN理解
自今年七月份以来,一直在实验室负责卷积神经网络(Convolutional Neural Network,CNN),期间配置和使用过theano和cuda-convnet.cuda-convnet2. ...
- 全卷积神经网络FCN理解
论文地址:https://people.eecs.berkeley.edu/~jonlong/long_shelhamer_fcn.pdf 这篇论文使用全卷积神经网络来做语义上的图像分割,开创了这一领 ...
- matlab中卷积convolution与filter用法
转自:https://blog.csdn.net/dkcgx/article/details/46652021 转自:https://blog.csdn.net/Reborn_Lee/article/ ...
- 什么是卷积convolution
定义 卷积是两个变量在某范围内相乘后求和的结果.如果卷积的变量是序列x(n)和h(n),则卷积的结果 , 其中星号*表示卷积. 当时序n=0时,序列h(-i)是h(i)的时序i取反的结果:时序取反使得 ...
- 向量的卷积(convolution)运算
一.向量的卷积运算 给定两个n维向量α=(a0, a1, ..., an-1)T,β=(b0, b1, ..., bn-1)T,则α与β的卷积运算定义为: α*β=(c0, c1, ..., c2n- ...
- 卷积 convolution
这东西大学学过,然后我忘记了,后来就只记得这个名字了. https://zh.wikipedia.org/wiki/%E5%8D%B7%E7%A7%AF http://www.guokr.com/po ...
- 彻底理解数字图像处理中的卷积-以Sobel算子为例
彻底理解数字图像处理中的卷积-以Sobel算子为例 作者:FreeBlues 修订记录 2016.08.04 初稿完成 概述 卷积在信号处理领域有极其广泛的应用, 也有严格的物理和数学定义. 本文只讨 ...
- 卷积神经网络CNN介绍:结构框架,源码理解【转】
1. 卷积神经网络结构 卷积神经网络是一个多层的神经网络,每层都是一个变换(映射),常用卷积convention变换和pooling池化变换,每种变换都是对输入数据的一种处理,是输入特征的另一种特征表 ...
随机推荐
- hadoop学习笔记411
安装hadoop 1. 免秘钥 使用hadoop用户 ssh-keygen -t rsa cp id_rsa.pub authorized_keys cat id_rsa.pub>&g ...
- elasticsearch2.x安装部署
目录 一.安装es以及插件 二.建立索引和映射,添加数据 三.备注 一.安装es以及插件 ElasticSearch-2.3.1版本,系统为CentOS 7.0位. 对应的网上下载地址都有: elas ...
- synchronized用法详解
1.介绍 Java语言的关键字,可用来给对象和方法或者代码块加锁,当它锁定一个方法或者一个代码块的时候,同一时刻最多只有一个线程执行这段代码.当两个并发线程访问同一个对象object中的这个加锁同步代 ...
- JAVA之BigInteger(转)【转】【很好用啊】
用Java来处理高精度问题,相信对很多ACMer来说都是一件很happy的事,简单易懂.用Java刷了一些题,感觉Java还不错,在处理高精度和进制转换中,调用库函数的来处理.下面是写的一些Java中 ...
- 使用c语言实现的常用函数
/* 为了面试准备的,有些在工作中也可以用用,本人算法方面比较欠缺,如果有更优秀的算法麻烦告诉我啊 */ /* strcat的实现 */ #include <assert.h> char* ...
- LIS与LCS的nlogn解法
LIS(nlogn) #include<iostream> #include<cstdio> using namespace std; ; int a[maxn]; int n ...
- Django中ORM外键和表的关系(Django编程-4)
外键 在MySQL中,表有两种引擎,一种是InnoDB,另外一种是myisam.如果使用的是InnoDB引擎,是支持外键约束的.外键的存在使得ORM框架在处理表关系的时候异常的强大.因此这里我们首先来 ...
- 洛咕11月月赛部分题解 By cellur925
听说是你谷史上最水月赛?我不听我最菜 T1:终于结束的起点 月天歌名好评 给你一个模数 \(M\),请你求出最小的 \(n > 0\),使得\(fib(n)\) \(mod\) \(m=0\), ...
- CentOS6.7上安装nginx1.8.0
主题: CentOS6.7上安装nginx1.8.0 环境准备: 1.gcc-c++ 示例:yum install gcc-c++ 安装:gcc-c++ gcc-c++编译工具 2.PCRE(Perl ...
- NET full stack framework
NFX UNISTACK 介绍 学习.NET Core和ASP.NET Core,偶然搜索到NFX UNISTACK,现翻译一下Readme,工程/原文:https://github.com/aumc ...
