#折半搜索，状压dp#nssl 1471 Y

---

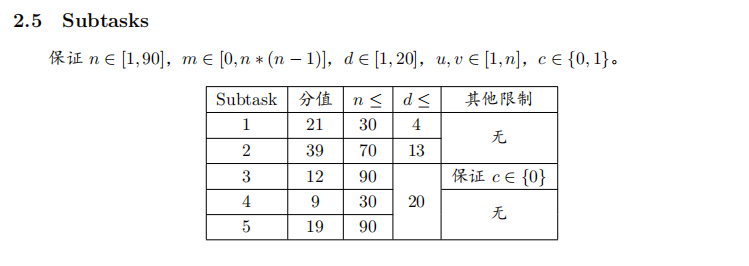
分析

设\(dp[i][j][s]\)表示从\(i\)到\(j\)的一条路径状态为\(s\)是否存在

但是这样肯定会T掉，考虑拼凑路径，分成两部分，

设\(dp[0/1][s]\)分别表示以某个起点/终点开始的一条路径状态为\(s\)是否存在，

现在表示一个点集，用出边的点集转移，可以用bitset维护，

然后如果\(dp[0][s]&dp[1][s']\)非空说明有中间点可以拼凑这两条路径

具体细节详见代码

---

代码

#include <cstdio>
#include <cctype>
#include <bitset>
#define rr register
using namespace std;
const int N=2048; int n,m,ans,t;
bitset<91>a[2][91],f[N],dp[N];
inline signed iut(){
	rr int ans=0; rr char c=getchar();
	while (!isdigit(c)) c=getchar();
	while (isdigit(c)) ans=(ans<<3)+(ans<<1)+(c^48),c=getchar();
	return ans;
}
signed main(){
	n=iut(); t=iut(); m=iut();
	while (t--){
		rr int x=iut(),y=iut(),z=iut();
		a[z][x][y]=a[z][y][x]=1;
	}
	rr int mid1=(m+1)>>1,mid2=m-mid1;
	for (rr int st=n;st;--st){
		for (rr int j=0;j<N;++j) f[j].reset();
		f[1][st]=1;
		for (rr int j=1;j<(1<<mid1);++j)
		for (rr int i=1;i<=n;++i) if (f[j][i])
		    f[j<<1]|=a[0][i],f[j<<1|1]|=a[1][i];
		for (rr int j=0;j<(1<<mid1);++j)
		    dp[j][st]=f[j|(1<<mid1)].any();
	}
	for (rr int i=0;i<(1<<mid1);++i)
	for (rr int j=0;j<(1<<mid2);++j)
	    ans+=(dp[i]&f[j|(1<<mid2)]).any();
	return !printf("%d",ans);
}