如何计算两个正太分布的KL散度 —— 正太分布的KL散度 (Kullback-Leibler divergence) 计算

参考：

https://blog.csdn.net/int_main_Roland/article/details/124650909

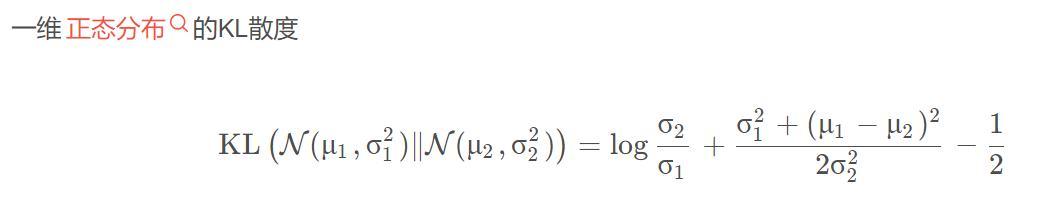
给出实现代码：

    def get_kl():
        mean0, log_std0, std0 = policy_net(Variable(states))

        mean1 = Variable(mean0.data)
        log_std1 = Variable(log_std0.data)
        std1 = Variable(std0.data)
        kl = log_std1 - log_std0 + (std0.pow(2) + (mean0 - mean1).pow(2)) / (2.0 * std1.pow(2)) - 0.5
        return kl.sum(1, keepdim=True)